| Россия, Ялта |
Методы и модели разработки управленческих решений в сервисной деятельности
Методы разработки управленческого решения в деятельности предприятия
Значение формальных методов разработки решения. Выше было установлено, что необходимость в разработке и принятии решений вызвана прежде всего динамичностью, случайностью и (или) неопределенностью условий работы компании, что находит выражение во влиянии на ее деятельность внешних и внутренних возмущений. Последние вмешиваются в деятельность предприятия, нарушают намеченный процесс его функционирования и могут расстроить обеспечение ресурсами. Поэтому управленческое решение направлено на погашение негативных последствий возникающих помех, нейтрализацию отклонений в ходе деятельности предприятия и сохранение выбранного режима продвижения к намеченным целям.
В этих условиях использование формальных методов в практике работы предприятия сферы услуг позволяет повысить объективность процесса поиска предпочтительных решений и улучшает их добротность. Компьютеризация не только рутинных, но и достаточно сложных творческих задач создает на предприятии "интеллектуальное пространство", которое поддерживается взаимодополняющим сочетанием знаний и опыта персонала с преимуществами новейших информационных технологий.
Не исчерпывая всего множества задач, выполняемых организацией сферы обслуживания, рассмотрим наиболее типичные из них с точки зрения того, насколько они оснащены математическими средствами. При этом сначала сосредоточим внимание на статических задачах, параметры которых остаются постоянными в течение определенного календарного периода, а затем коснемся динамических задач, отличающихся изменяемостью параметров во времени.
Статические задачи разработки управленческого решения в условиях определенности. Разработка решений в условиях определенности исходит из признания того, что реализация некоторого решения приведет к однозначному и известному наперед результату. Предпосылкой этому служит наличие всей необходимой и точной информации о будущем состоянии внешней и внутренней среды, что и дает основание для подобного рода уверенного заключения.
В связи со сказанным выше следует заметить, что "камнем преткновения" для применения вычислительных методов нередко становится располагаемый объем информации. Если по этой причине прогнозные разработки отсутствуют, предприятие лишается возможности формировать перспективные планы. Вот почему компании часто пренебрегают составлением планов на длительный период, ограничиваясь принятием лишь краткосрочных и оперативных планов.
Так, на предприятиях питания часто не налажено информационное обеспечение плановой работы, существуют недостатки в учете и отчетности1, вследствие чего не формируются планы по приобретению и расходу сырья и покупных товаров. В отчетных документах не регистрируется информация о фактическом поступлении отдельных видов сырья и покупных товаров, о товарных запасах в ассортиментном разрезе. Многие предприятия работают вообще без планов хозяйственной деятельности.
Планирование объемов реализации услуг в таком случае проводится по принципу "от достигнутого": исходной базой для показателей плана являются полученные результаты за аналогичный период в прошлом. При этом устанавливаемые плановые показатели не обязательно повторяют их фактические значения за соответствующий период, поскольку они могут быть скорректированы с учетом ожидаемых в будущем изменений. Подобные наметки показателей не имеют под собой рациональных правил обоснования и продиктованы субъективными соображениями, интуицией и опытом управленческого персонала.
Между тем наличие необходимых исходных данных открывает возможность привлечения математических методов нахождения плановых решений. Достаточное распространение среди таких методов получили так называемые классические методы отыскания решений, основанные на приемах математического анализа. В том случае, если появляется необходимость минимизировать или максимизировать некоторый экономический показатель и он представляет собой непрерывную функцию с частными производными до второго порядка включительно, можно воспользоваться известными методами поиска экстремума функции. Дифференцируя эту функцию и приравнивая нулю ее производную, определяют искомое значение переменной, при котором функция имеет минимум или максимум.
Приложение этого метода иллюстрируют задачи управления запасами предприятия, когда требуется найти такое решение по заказу сырья, которое было бы обоснованным с точки зрения бесперебойного снабжения производственного процесса и затрат на прием и хранение сырья. Такие задачи характерны для предприятий, использующих в своем технологическом процессе покупные ингредиенты, завозимые на склад.
Например, предприятия питания образуют текущие товарные запасы сырья, полуфабрикатов и покупных товаров, завышение которых ведет к ухудшению качества и порче продуктов, росту товарных потерь и издержек производства и обращения, а занижение - к их дефициту и снижению объема товарооборота. Используя описанный математический метод, удается отыскать величину и периодичность поставок, обеспечивающих наименьшее значение затрат на прием и хранение заказа.
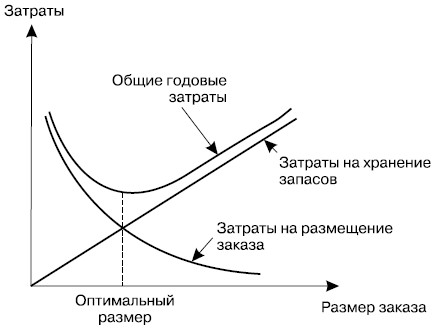
Эту же задачу можно поставить и в несколько иной форме2. А именно: определить экономичный размер заказа, при котором общие затраты на хранение запасов (арендная плата за помещение, страховые взносы, коммунальные услуги) и размещение заказа на закупку и поставку хранимого товара на склад были бы возможно минимальными. При этом немаловажно следующее обстоятельство: чем больше размер заказа, тем выше затраты на его хранение, но сокращаются расходы на размещение заказа (в течение длительного периода число контактов с поставщиками уменьшается); и наоборот, чем меньше размер заказа, тем ниже затраты на его хранение, но зато больше расходов на размещение заказа (рис. 27.2). Вот почему оптимальный размер заказа товара будет отвечать минимуму общих годовых затрат.
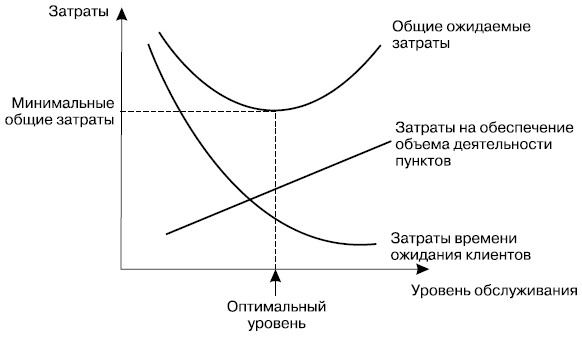
Аналогично можно рассуждать и в отношении затрат обслуживающих пунктов и клиентов, обратившихся к ним для совершения определенных операций. Действительно, с одной стороны, процесс обслуживания требует затрат для своего осуществления, а с другой стороны, из-за ожидания в очереди несут затраты и клиенты. В результате образуются суммарные затраты и, очевидно, чем они меньше, тем лучше организован процесс обслуживания. Минимум общих ожидаемых затрат и будет соответствовать оптимальному уровню обслуживания (рис. 27.3).
Вполне очевидно, что при разработке управленческих решений необходимо учитывать реальные ресурсные возможности предприятий. Поиск предпочтительного планового решения должен осуществляться в рамках располагаемого запаса сырья, материалов, рабочей силы, финансов, информации и других ресурсов, которые ограничивают пространство допустимых решений. Формализуя эти условия, математические методы позволяют найти объем предоставляемых услуг, отвечающих выдвигаемому критерию и требованию баланса. В практике работы предприятий широко применяются методы балансирования затрат, выручки или запаса ресурсов и потребности в них.
Для поиска объема оказываемых услуг, который обеспечивает безубыточную деятельность, используют аппарат линейной алгебры. С помощью уравнения постоянные и переменные расходы предприятия связываются в линейной форме с выручкой от реализации услуг. Удовлетворяя требованию покрытия затрачиваемых средств, уравнение позволяет определить критический объем услуг (соответствующий на графике "точке безубыточности"), оказание которых выводит предприятие на режим полного погашения понесенных издержек. Дальнейшее наращивание объема оказываемых услуг приводит к получению прибыли от их реализации.
В том случае, если существует информация о нормах расхода ресурсов на единицу производимых услуг, можно воспользоваться линейными функциями для описания баланса между потребными и имеющимися ресурсами (например, между необходимым по плану объемом сырья и его запасом на предприятии). Следующим шагом становится отыскание объема услуг, который, с одной стороны, не нарушает этого баланса, а с другой - доставляет экстремальное (минимальное или максимальное) значение выбранным экономическим показателям (выручке, затратам, прибыли и др.) деятельности предприятия. Тем самым настоящая задача приобретает оптимизационный характер, поскольку направлена на поиск наиболее выгодного объема услуг различного вида в рамках наложенных ресурсных ограничений (с добавлением при необходимости нижнего и верхнего пределов спроса на виды услуг).
В общем виде такая задача содержит критериальную функцию оптимизируемого экономического показателя, неравенства, выражающих ресурсные и иные ограничения, и получила название неклассической (в отличие от классической, не имеющей ограничений типа неравенств) задачи. Чаще всего рассматриваемая задача планирования объема оказываемых услуг формулируется в однокритериальной статической детерминированной постановке. Иными словами, в качестве критерия оптимальности принимается один экономический показатель (обычно прибыль, реже выручка, затраты и др.), а элементы задачи (нормы расхода и запас ресурсов, пределы спроса) не учитывают влияния времени и случайных факторов. В итоге задача описывается в терминах хорошо известного метода математического программирования, называемого линейным программированием, и может быть решена симплекс-методом.
Примером подобной задачи может служить оптимизация производственной программы предприятия питания, позволяющая найти объемы выпуска блюд, реализация которых при заданных ресурсах даст максимально достижимую прибыль. Для решения такой задачи потребуется информация о прибыли от продажи одного блюда, о нормах расхода сырья, покупных товаров, времени (трудоемкости) и других ресурсов на изготовление одного блюда и располагаемых объемах этих ресурсов. Кроме того, уместными могут оказаться ограничения на выпуск блюд исходя из прогнозируемых значений минимально и максимально возможного спроса клиентов на эти блюда.
Вместе с тем деятельность предприятия направлена на достижение множества целей, поэтому может потребоваться оптимизация не по одному, а по нескольким критериям одновременно, к тому же нередко противоречащим друг другу. Тогда задача становится многокритериальной, и для ее выполнения можно предложить по меньшей мере три варианта постановки3.
1. Формирование обобщенной критериальной функции. Этот вариант связан с оцениванием приоритета каждого критерия (ведь критерии могут иметь неодинаковую важность для предприятия) и объединением критериальных функций в одной обобщенной функции. Результат решения этой задачи определяется присвоенными приоритетами и в случае рассогласования (противоречивости) критериев является компромиссным, так как отвечает в той или иной степени всем критериям сразу. Варьируя величинами приоритетов в зависимости от предпочтений руководителя, можно добиться приемлемого варианта плана (объемов оказываемых услуг и расходуемых ресурсов), удовлетворяющего заданным ограничениям и приоритетам критериев.
Для иллюстрации многокритериальной постановки может быть предложена задача, о которой шла речь выше. Руководство предприятия преследует две цели - максимума объема продаж и максимума конкурентоспособности оказываемых услуг - одновременно, и тем самым задача формулируется как двухкритериальная. В том случае, если цена на услугу строго соответствует ее конкурентоспособности (чем выше конкурентоспособность услуги, тем больше на нее цена, и наоборот), задача упрощается и сводится к однокритериальной. Действительно, в такой ситуации максимизация объема продаж гарантирует максимизацию общей конкурентоспособности услуг и поэтому один из критериев может быть опущен. В ином случае, когда такая зависимость между конкурентоспособностью и ценой на услугу не соблюдается, максимизация объема продаж не приведет к достижению максимально возможной общей конкурентоспособности всех реализуемых услуг. В этом смысле критерии противоречат друг другу, и оптимизируемый план оказания услуг должен будет отвечать обоим критериям лиш ь в определенной степени, т. е. становится компромиссным. Назначая и изменяя величину приоритета каждого критерия, можно получить большее соответствие плана одному критерию и меньшее - другому в зависимости от их важности.
2. Метод последовательных уступок заключается в том, что в качестве оптимизируемой критериальной функции выбирается один из показателей эффективности, а другие показатели эффективности переводятся в состав ограничений и для них устанавливаются предельные (наименьшее, наибольшее) значения. Полагая, что показатели эффективности имеют противоречивый характер, и варьируя их предельные значения в одном направлении (по нарастанию или убыванию), наблюдают за изменением оптимизируемого показателя в ином направлении. Тем самым, допуская приемлемое ухудшение величины одного показателя эффективности, добиваются улучшения величины другого показателя.
Решение настоящей задачи осуществляется в многоэтапном режиме.
- Проводят вариантные расчеты с выбранным критерием - показателем эффективности, меняя в каждом варианте предельные значения для остальных показателей эффективности. Такой уступкой значениям одного показателя эффективности получают ряды связанных между собой величин всех показателей эффективности.
- Производится выбор нового показателя эффективности для критериальной функции, а на прежний оптимизируемый показатель накладывается ограничение. Выполняя подобные расчеты при уступке другому показателю, формируют аналогичный ряд зависимых друг от друга величин различных показателей эффективности.
- Вновь меняется оптимизируемый показатель эффективности (если их в задаче более двух) и вводится ограничение на предыдущий критериальный показатель, повторяются те же расчеты, и так до тех пор, пока не будет проведена оптимизация по всем показателям эффективности.
- Упорядочивают (обычно по возрастанию значений одного из показателей эффективности) и сводят в таблицу полученные на всех этапах ряды значений показателей эффективности. Затем аналитики или ЛПР (лицо, принимающее решение) сообразно своим представлениям об оптимальном плане оказания услуг отдают предпочтение тому или иному компромиссному варианту расчета.
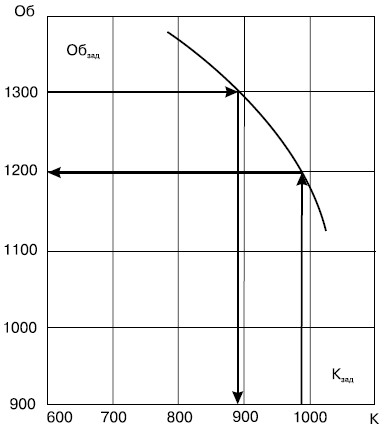
Для пояснения сущности метода последовательных уступок сошлемся на следующий пример4. Пусть требуется найти план оказания услуг, оптимальный с позиций двух критериев: объема производства (в рублях) и общей (суммарной) конкурентоспособности (в баллах) предоставляемых услуг. И тот и другой критерий необходимо максимизировать, но поскольку по условию задачи улучшение одного из них приводит к ухудшению другого, оптимальный план приобретает компромиссный характер. В процессе поэтапного решения этой задачи определяют пары связанных между собой значений объема производства (Об) и общей конкурентоспособности (К), точки которых для наглядности наносят на плоскость.
Образованная в результате этого линия раскрывает взаимосвязь оптимизируемых показателей объема производства (Об) и общей конкурентоспособности (К) и отображает их противоречивость: увеличение одного из них достигается только за счет уменьшения (уступки) другого, и наоборот. Наряду с этим появляется возможность, задавая значение одного из них (объема производства Обзад или общей конкурентоспособности Кзад), отыскать соответствующее ему значение другого показателя. В итоге, делая уступку по одному показателю и получая взамен рост другого, находят удовлетворительный компромиссный вариант плана.
3. Многоцелевое программирование. Этот способ решения многокритериальной задачи при расхождении величины потребных ресурсов и их запаса позволяет отыскать наилучший план либо величину недостающего объема ресурсов для того, чтобы обеспечить баланс необходимых и располагаемых ресурсов и найти искомый оптимальный план с учетом всех критериев.
Подытоживая обсуждение задач в условиях определенности, нелишне напомнить, что их постановка игнорирует влияние случайных факторов на процесс реализации решения, и данное обстоятельство необходимо принимать во внимание на практике. Вследствие этого интерес представляет формулирование задачи с учетом вероятностного характера действия рисковых факторов, что повышает достоверность разрабатываемых управленческих решений и их пригодность в деятельности предприятия.
Статические задачи разработки управленческого решения в условиях риска. Разработка решений в условиях риска основывается на обработке статистической информации и связывает выполнение решения с множеством возможных исходов, имеющих определенную и известную аналитикам вероятность появления. Поэтому предпочтительным будет то решение, которое в среднем дает лучший результат (максимально достижимую прибыль, выручку, минимальные затраты и т. д.) или наибольшую вероятность соблюдения некоторого условия (например, того, что прогнозируемая прибыль будет не меньше наперед заданной пороговой величины). Следует подчеркнуть, что, поскольку из-за влияния случайных факторов фактическая величина критериального показателя при многократном повторении будет иметь разброс значений, резонно вести речь об оптимизации лишь его средней величины.
Это означает, что отдельная реализация принятого решения по своему результату может быть не только лучше, но и хуже, чем у другого решения. Однако, когда решение реализуется в одинаковых условиях многократно, отклонения результата в ту и иную сторону взаимно погашаются и осредненный показатель эффективности окажется предпочтительнее по сравнению со всеми другими решениями.
Так, при планировании одного и того же ассортимента и объемов услуг выручка и прибыль от оказания услуг каждый раз может меняться, быть меньше или больше расчетной величины в силу случайного характера изменения среды (колебания уровня спроса, инфляции, издержек производства, непоставок сырья и задержек с оплатой за оказанные услуги, брака, поломок оборудования, болезни работников и др.). В этой ситуации приходиться выбирать такой план предоставления услуг, который отличается от других большей средней выручкой или прибылью.
Постановка подобных задач становится возможной лишь при наличии у аналитиков статистических сведений о динамике в прошлом исходных данных задачи, отвечающих требованиям необходимого объема и точности. При этом предполагается, что выявленная закономерность изменения этих данных и в будущем останется такой же, сохраняя предсказуемым прогнозный фон и позволяя тем самым надеяться на реальность ожидаемых результатов в планируемом периоде.
Математический аппарат задач разработки решений в условиях риска базируется на использовании методов теории вероятностей и ее приложений.
Привлечение этих методов позволяет выбрать предпочтительное решение в разнообразном спектре практических ситуаций. В одних ситуациях становится возможным оценить уровень риска при предоставлении услуг (например, найти вероятность оказания определенного количества услуг или погашения задолженности за произведенные услуги), в других ситуациях - рассчитать вероятность того, что показатель экономической эффективности при освоении новой услуги будет не меньше заданного предельного значения и т. д.
Применение метода стохастического программирования к описанной выше схеме линейной оптимизации дает вероятностное описание критериальной функции и функций ограничений на ресурсы. Благодаря этому удается учесть изменение экономических показателей, вызванных действием рисковых факторов. В частности, цена, затраты, прибыль, нормы расхода ресурсов на одну услугу и запас ресурсов могут иметь разброс значений ввиду влияния различных вероятностных причин (инфляции, изменения платежеспособного спроса клиентов, конкуренции, нарушения технологии, перебоев с поставками сырья или отказа от них и др.).
Можно предложить два подхода к формированию критериальной функции, получивших название М-постановки (модели) и Р-постановки (модели)5.
При М-постановке оптимизируемая критериальная функция представляет собой среднюю величину (называемую математическим ожиданием) показателя эффективности (прибыли, выручки, затрат и др.).
При Р-постановке максимизируется вероятность того, что показатель эффективности будет не меньше или не больше заданного предельно допустимого значения.
Стохастическая постановка ограничений на потребляемые ресурсы также может быть двух видов.
Первый вид с помощью неравенства формализует то обстоятельство, что средний расход ресурсов при оптимальном плане не должен превышать имеющийся средний запас их на предприятии.
Второй вид постановки ограничений вводит следующее отношение: вероятность того, что расход ресурсов на предприятии не превысит его располагаемый запас, не должна быть ниже заданного уровня. Или наоборот, т. е. вероятность того, что будет иметь место нехватка ресурсов, окажется не выше установленного уровня.
Остановимся подробнее на М-постановке задачи стохастического программирования. Она включает в себя:
- критериальную функцию, посредством которой минимизируется или максимизируется средняя величина показателя эффективности;
- ресурсные ограничения, имеющие вероятностный вид: вероятность того, что потребность в ресурсах будет покрыта их запасом на предприятии, не должна быть ниже заданного уровня;
- ограничения на область изменения объемов предоставляемых услуг, т. е. они должны быть в пределах (от минимума до максимума включительно) прогнозируемого спроса.
В процессе выполнения задачи рассчитываются оптимальные объемы услуг и соответствующая им величина показателя эффективности. Анализ полученного решения, удовлетворяющего критериальной функции и наложенным ограничениям, приводит к следующим выводам.
- Чем жестче требования к соблюдению ресурсных ограничений (выше задаваемый уровень вероятности их соблюдения), тем больше должен быть запас этих ресурсов на предприятии. И это понятно: для большей уверенности в том, что план оказания услуг не будет сорван из-за дефицита ресурсов, запас последних должен быть достаточным. При отсутствии дополнительных ресурсов объем предоставляемых услуг может уменьшиться, и тогда ухудшится значение показателя эффективности.
- Чем больше разброс (дисперсия) значений текущего запаса ресурсов, тем выше необходимость иметь дополнительные ресурсы для гарантии предоставления рассчитанных оптимальных объемов услуг.
Методы теории вероятностей находят широкое применение не только при планировании объемов услуг, но и в ряде других задач, учитывающих действие стохастических факторов. Например, при разработке решений, связанных с обеспечением надежности оборудования предприятия. Принимая во внимание случайный характер выхода из строя оборудования, можно оценить ожидаемые издержки и исходя из этого выбрать выгодный вариант покупки (комплект) запасных частей к этому оборудованию.
Другой метод - динамическое программирование (один из разделов математического программирования) - позволяет при выполнении некоторых условий выбрать решение в ситуации, когда исследуемый процесс развивается во времени и (или) может быть представлен последовательностью отдельных шагов. При этом на каждом шаге вычисляются последствия принятия тех или иных решений и определяется наилучший вариант действий на перспективу.
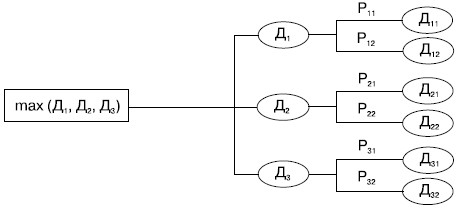
Продемонстрируем этот метод с помощью дерева решений, раскрывающего во времени логическую структуру процесса разработки решения. Принимаем во внимание, что развертывание этого процесса происходит как обычно (слева направо), а ход самого анализа протекает в обратном направлении, т. е. справа налево. Предположим, из трех решений необходимо выбрать наиболее доходное и по каждому решению известны величины доходов и вероятность их получения: при реализации первого решения предприятие прогнозирует доход Д11 с вероятностью Р11 или доход Д12 с вероятностью Р12, второго решения - доход Д21 с вероятностью Р21 или доход Д22 с вероятностью Р22, третьего решения - доход Д31 с вероятностью Р31 или доход Д32 с вероятностью Р32 (см. рисунок). Двигаясь по ветвям дерева справа налево, вычисляем средний доход (Д1, Д2, Д3) по каждому решению по формуле математич еского ожидания (например, Д1 = Р11 x Д11 + Р12 x Д12), а затем наибольшее из рассчитанных доходов Д1, Д2, Д3 укажет на предпочтительное решение.
Анализ решения
Метод динамического программирования может быть использован, например, при выборе решений в задаче освоения нового вида изделий или услуги. Полагая, что этот процесс является многовариантным (варианты: отказ от освоения, массовое или экспериментальное производство изделий, услуг) и может быть разложен на ряд этапов, в зависимости от достигнутого результата на каждом этапе удается (благодаря статистической информации) оценить ожидаемую прибыль предприятия и выбрать предпочтительное решение.
Для принятия решений в условиях риска может быть предложен метод Монте-Карло (его называют также методом статистических испытаний), который представляет собой способ моделирования анализируемого процесса, на который оказывают влияние вероятностные факторы. Достоинства этого метода становятся очевидными, когда наблюдать за реальным процессом затруднительно или невозможно. В подобных обстоятельствах он позволяет искусственно воссоздать ("разыграть") интересующую ситуацию с помощью механизма случайного выбора значений параметров задачи.
Так, методом Монте-Карло можно воспроизвести процесс обслуживания клиентов на предприятии питания, автосервиса, в парикмахерской, библиотеке и т. д. Длина очереди, время обслуживания клиентов имеют случайный характер и могут быть получены генерированием их значений специальными программами на ЭВМ (генераторами случайных чисел). Тем самым решения по организации предприятия могут быть приняты путем математического моделирования без обращения к натуральному эксперименту.
Метод теории массового обслуживания дает возможность изучать потоки заявок (заказов клиентов) и процесс их удовлетворения. Последовательность поступающих заявок образует очередь, которую заявка покидает или ждет, пока не наступит ее время. Сам процесс поступления заявок является вероятностным, поскольку момент их прихода произвольный, как и в реальной жизни.
Удовлетворение заявок выполняют пункты обслуживания, которые могут ожидать заявку или быть заняты. Очевидно, скопление заявок в очереди приводит к потерям времени клиентов и перегрузке каналов, а отсутствие заявок - к простою пунктов и излишним затратам на их содержание.
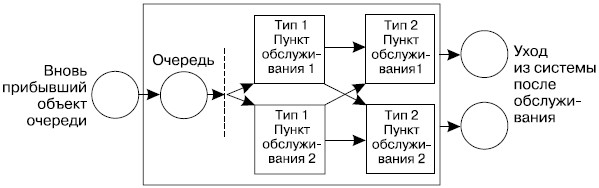
В зависимости от содержания процесса оказания услуг находят применение системы массового обслуживания различного класса. Обычно они классифицируются по числу каналов (пунктов обслуживания) - на одноканальные и многоканальные; по числу фаз (стадий) обслуживания - на однофазные и многофазные. Примером одноканальной однофазной системы (рис. 27.4) может служить работа читального зала библиотеки, почтового отделения или гардероба в том случае, если единственный работник выполняет полное обслуживание обратившихся к нему людей.
К многоканальной однофазной системе (рис. 27.5), в частности, относится группа кассиров, взимающих в магазине плату у покупателей из одной очереди, парикмахерская или автосервис с взаимозаменяемыми мастерами.
Одноканальную многофазную систему (рис. 27.6) представляет столовая, если поток посетителей обслуживается его работниками вдоль одной продуктовой линии. Аналогично организуется работа во время медицинского осмотра призывников или автолюбителей, последовательно проходящих контроль у специалистов разного профиля (невропатолга, окулиста, хирурга и др.). Вместе с тем эта система становится многоканальной многофазной (рис. 27.7), если перед началом осмотра поток клиентов "распараллеливается" и работают два и более "конвейера" обслуживания.
Основные показатели системы массового обслуживания:
- среднее время, проводимое клиентом в очереди;
- средняя длина очереди;
- среднее суммарное время ожидания и обслуживания;
- среднее количество клиентов в системе;
- вероятность того, что пункт обслуживания будет простаивать;
- коэффициент использования системы.
Таким образом, применяя этот метод, можно проектировать или рационализировать организацию системы массового обслуживания и обосновать число каналов с позиций эффективности ее работы.
Статические задачи разработки управленческого решения в условиях неопределенности. Разработка решений в условиях неопределенности осуществляется тогда, когда исходная информация о деятельности предприятия и среды не отвечает требованиям допустимого объема и точности. Иными словами, необходимые для задачи сведения отсутствуют или страдают ограниченностью, и (или) их ценность для будущих решений вызывает сомнения.
По сравнению с принятием решений в условиях риска ситуация неопределенности становится еще более запутанной: если в рисковой ситуации предприятие располагает статистической информацией относительно факторов среды, то в неопределенной обстановке достаточной и убедительной информации о них нет. Поэтому принимающий решение не может достоверно оценить его последствия, и ему приходится мириться с наличием неизвестных факторов, влиять на которые предприятие не может.
Такая неопределенность параметров среды характерна для нынешнего состояния отечественной экономики. За пределами компетенции большинства предприятий находится изменение уровня инфляции, валютного курса рубля, динамика финансовых процессов на крупных биржах, меры конкурентов и другие факторы. Отсутствие надлежащей "прозрачности" среды и приводит к тому, что принятие решений в обстановке неопределенности - наиболее распространенный способ действий руководителей предприятий на современном этапе.
Существующие методы принятия решений в условиях неопределенности, характеризующейся отсутствием полной и точной исходной информации, не дают возможности однозначно выбрать предпочтительное решение. Каждое рассматриваемое решение окружено "туманом", и его реализация может привести к тем или иным последствиям. Однако эти методы позволяют отчасти снизить субъективизм в процессе разработки решения и предлагают правила разумного выбора.
В практической деятельности предприятия ситуация стратегической неопределенности нередко складывается из-за участия в ней нескольких сторон, преследующих свои цели. Подобные задачи именуют многосторонними, и по своему содержанию они напоминают игровую ситуацию: каждая сторона придерживается собственной стратегии и может делать свой ход. В результате итог этой игры (выигрыш или проигрыш каждой стороны) зависит от действий всех участвующих в ней сторон.
Аналогия с игрой послужила стимулом для разработки специальных игровых методов обоснования таких решений - теории статистических решений, теории игр и минимакса.
Методы теории статистических решений (игр) находят применение при действии вероятностных факторов. В этом случае участником игры становится сама природа, т. е. объективная действительность, лишенная какого-либо замысла сознательного противодействия намерениям другого участника игры. В качестве таких природных факторов могут выступать макроэкономические условия хозяйствования: уровень покупательной способности клиентов, сложившийся на рынке спрос на продукцию или услуги и др. Иллюстрацией такой задачи может служить выбор решения предприятия об освоении нового вида изделий или услуги при различных предположениях относительно будущей рыночной конъюнктуры. Удачным решением будет признано то, при реализации которого ожидается наибольшая прибыль предприятия.
Аппарат теории игр и минимакса также используется в ситуации со стратегическими неопределенностями. В ней довольно часто интересы участников игры могут различаться, и тогда несовпадение целей порождает их конфликт (конфликтные задачи). Противоположные цели участников приводят к появлению антагонистических задач принятия решений, в ином случае они по-прежнему будут неантагонистическими (поэтому их еще называют играми с непротивоположными интересами).
Методы теории игр позволяют выбрать решение в условиях многократно повторяющегося конфликта равноправных участников (не связанных друг с другом какими-либо формами подчинения, т. е. находящихся на одном уровне власти). Например, подобная задача возникает в ходе конкурентной борьбы двух предприятий: оба они находятся перед выбором решения, которое максимизировало бы доход или минимизировало убыток, - оставить качество оказываемой услуги прежним, улучшить его или освоить новый вид услуги. Заметим, что величина ожидаемого дохода или убытка каждого из участников зависит от выбора стратегий руководителями обоих предприятий. Поскольку ни один из них не знает о подлинных намерениях другого, ничего иного в этих обстоятельствах не остается, как принять наиболее осторожное решение.
Наконец, методы теории минимакса применяются для анализа конфликтных антагонистических ситуаций, повторяющихся один или ограниченное число раз.
Задачи принятия решений в условиях концептуальных неопределенностей базируются на применении эвристических методов и метода "дерева целей". Факторы задачи трудно измерить и формализовать, поэтому приходится обращаться к квалифицированным специалистам, обладающим профессиональным опытом и интуицией, и пользоваться их мнением для выбора решения. Тем самым экспертные суждения дают возможность ослабить информационную неполноту задачи, хотя и остаются при этом субъективными по своему характеру.
Среди таких подходов известны методы "мозговой атаки" (коллективной генерации идей), "сценариев", "Дельфи", экспертных оценок и другие6. Очевидно, эти методы могут быть полезны при изобретении оригинальных видов изделий или услуг, модернизации технологии, прогнозе тенденций изменения рыночной конъюнктуры, анализе перспектив развития предприятия и др.
В своей практике эксперты часто занимаются численным оцениванием параметров, событий, явлений, процессов и т. п. , непосредственное измерение которых затруднительно. Причем к методу экспертных оценок прибегают не только при неопределенной ситуации разработки решений, но и в других задачах, когда формальные приемы отступают перед сложностью проблемы. Например, в детерминированных многокритериальных задачах с помощью экспертного оценивания вводятся приоритеты (меры важности) оптимизируемых критериев. В аналогичной задаче с противоречивыми критериями эксперт может участвовать в выборе компромиссного варианта решения.
В условиях неопределенности с помощью экспертных оценок (в литературе их иногда называют субъективными вероятностями) и вероятностных методов удается проанализировать возникшую неопределенную ситуацию и принять обоснованное решение. Так, пользуясь известной в теории вероятностей формулой Т. Байеса, можно произвести переоценку вероятности того или иного варианта действий конкурента при поступлении дополнительной информации о нем. Подобным способом, например, вычисляется вероятность освоения конкурентом новой услуги, когда становятся ясными его намерения относительно своего материально-технического развития.
В многовариантных задачах по вероятностному критерию можно выбрать решение, имеющее больше шансов на успех по сравнению с другими рассматриваемыми решениями. В таких случаях по принятому критерию (математического ожидания, П.С. Лапласа, А. Гурвица) сравниваются возможные решения, и предпочтение остается за тем из них, которое дает лучшее численное значение, например, в ситуации с выбором решения по освоению нового вида услуг при разной прогнозируемой реакции клиентов на нее.
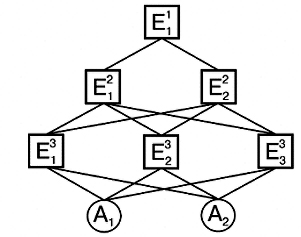
Другой метод, получивший название "дерево целей", позволяет раскрыть процесс реализации цели предприятия, решения проблемы и представить его в виде разветвленной иерархической структуры (рис. 12.8). На основании анализа существующих связей и отношений подчинения происходит разложение цели на подцели, те, в свою очередь, разделяются на подцели следующего уровня и т. д. вплоть до порождения требуемых элементов (функций, задач, альтернатив и т. д.), обеспечивающих достижение цели. Такое разукрупнение дает наглядную картину о способе движения к цели и возможность проанализировать необходимые для этого ресурсы и действия.
Так, на рис. 27.8 представлена иерархическая структура, на верхнем ярусе которой указана цель, затем на двух промежуточных уровнях располагаются необходимые для ее достижения подцели и на самом нижнем уровне - альтернативы А1 и А2, обеспечивающие достижение цели7.
Удобный способ представления структуры многоэтапных процессов принятия решений - "дерево решений": ветви его отображают различные события, а узлы (вершины) - состояния, в которых производится выбор решения. В одних состояниях этот выбор осуществляет человек, в других - сама "природа", т. е. со стороны среды имеет место случайный выбор с той или иной вероятностью исхода (например, успеха или неудачи при организации, реорганизации бизнеса или предложении потребителям нового вида изделий, услуг и т. п.). Подобная структуризация задачи помогает обосновать предпочтительный вариант действий при конечном числе этапов и решений.
Популярность и практичность экспертных методов обусловлена и тем, что процесс компьютерного моделирования остается слабо восприимчивым к ценному опыту персонала, накопленному им при повседневном управлении предприятием. Достаточно редко еще эвристические соображения могут быть изложены математически и запрограммированы в моделях поиска решений. Подобные модели из-за отсутствия средств формализации субъективных представлений человека чаще всего обслуживают лишь стандартные экономические расчеты.
К настоящему времени уже создан инструментарий для того, чтобы придать моделям свойственную нашему рассудку способность к восприятию и оперированию не только количественной, но и не всегда четко определенной качественной информацией. Моделирование приобретает искомую конструктивность, а сами модели - добротность в практической работе, с усилением их средствами интеллектуализации, которые предоставляют приложения интенсивно развивающейся ныне теории нечетких множеств8. В рамках этих приложений удается описать приближенный характер качественной информации: ведь исходные данные для моделей в подвижной среде чаще всего неточны и к тому же расплывчаты, поскольку несут печать нечеткости мышления человека. Однако только человек является источником "неформальных" сведений о среде и наиболее полно выражает ее экспертную оценку на естественном языке. На этом основании эвристическая информация описывается с помощью специальных лингвистических переменных, передающих оттенки субъективного суждения в алгори тм модели.
Говоря конкретнее, нечеткое множество задается функцией принадлежности (обозначается символом m), которая указывает степень принадлежности (числом от 0 до 1 включительно) некоторой переменной x к данному нечеткому множеству.
Например9, пусть лингвистическая переменная "прирост прибыли" с числовой областью от 100 тыс. руб. до 1 млн руб. может принимать значения "низкий прирост", "средний прирост", "высокий прирост". Очевидно, что границы между этими лингвистическими значениями размыты, и переход от низкого прироста к среднему, а затем к высокому совершается плавно и постепенно. Это свойство непрерывности формализует вводимая аналитиками функция принадлежности m, сообщая, например, что прирост прибыли, равный 300 тыс. р., относится к низкому со степенью 0,6 и среднему со степенью 0,3. Вместе с тем прирост прибыли 700 тыс. р. принадлежит к среднему со степенью 0,2 и высокому со степенью 0,7.
Как видно из примера, аппарат нечетких множеств позволяет количественно оценить (с помощью значений функций принадлежности 0,6, 0,3, 0,2 и 0,7) качественные суждения о прибыли "низкий прирост", "средний прирост", "высокий прирост". Вследствие этого математические операции в алгоритмах поиска решений охватывают как числовую, так и нечисловую информацию, имеющуюся у аналитиков.
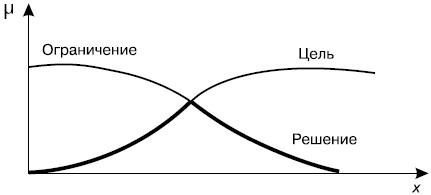
Показательно применение нечетких множеств и для обоснования оптимального решения, когда исходные данные носят размытый характер. При такой ситуации стирается различие между намеченными целями и ограничениями, в результате чего довольно просто проводить их согласование и находить решение. Ведь в этом случае и цель, и ограничения описываются одинаковым образом. А значит, и оптимальное решение, которое отыскивается в пространстве альтернатив, становится размытым и образуется пересечением неточно заданных целей и ограничений10 (рис. 27.9).
Так, цель предприятия может выражаться следующим расплывчатым образом: "Занимать более или менее значительную долю на региональном рынке туристических услуг" или "Сохранить достаточную конкурентоспособность оказываемых услуг". Аналогично и накладываемые в задаче ограничения могут иметь нечеткую формулировку: "Получаемый доход или прибыль не должны сильно снижаться" или "Не допускать большой перегрузки работы персонала". Найденное в этой неопределенной ситуации решение, очевидно, тоже будет размытым, что и отвечает ожиданию управленческого персонала.
Тем самым применение теории нечетких множеств дает возможность обращаться с трудно формализуемыми эвристическими сведениями, в связи с чем управленческое решение аккумулирует в себе как количественную, так и качественную информацию. Благодаря этому решение становится более полноценным и в большей степени подходит для реализации в деятельности предприятия в условиях присущей рыночной среде неопределенности.
Динамические задачи разработки управленческого решения. Все рассмотренные выше задачи разработки решений являются статическими, поскольку их элементы не зависят от времени и остаются постоянными в течение некоторого календарного периода. Между тем в действительности параметры могут непрерывно меняться произвольным образом, и это обстоятельство привело к постановке динамических задач. Так, цены на потребляемые ресурсы и производимые изделия и услуги, уровень спроса на них и т. д. находятся в движении, что и заставляет учитывать их изменчивость в процессе поиска решений.
Для разработки решений в условиях определенности служат методы теории оптимальных процессов. Среди них - вариационное исчисление, занимающееся исследованием условий минимума или максимума величин, значение которых зависит от выбора одной или нескольких функций. Средства этого исчисления дают возможность отыскать функцию, доставляющую оптимальное значение некоторому экономическому критерию.
Например, для минимизации общих издержек производства и содержания запаса изготовленной продукции необходимо найти отвечающую этому требованию функцию производства продукции (зависимость объема ее выпуска от времени). Подобная задача может быть характерна для деятельности предприятия питания, приготовляющего и складирующего часть своей продукции для продажи населению.
При разработке решений в условиях риска применяют методы теории случайных процессов. Под последними понимают изменение поведения системы во времени под влиянием случайных факторов, причем вероятность каждого варианта протекания процесса известна. Решения в условиях риска вынуждены разрабатывать предприятия питания и бытового обслуживания, автозаправочные станции, библиотеки и другие учреждения сервиса.
В самом деле, число обратившихся за обслуживанием клиентов, образование очереди и ее длина, время ожидания клиентов в очереди и продолжительность оказания услуги - все эти параметры являются случайными и могут непрерывно меняться с течением времени. Поэтому методы теории случайных процессов используются в задачах массового обслуживания и позволяют принять обоснованное решение по организации деятельности предприятия сферы услуг.
Другим средством поиска решений в рисковой ситуации служат методы статистической динамики систем управления. С их помощью удается исследовать влияние случайных возмущений на динамику поведения предприятия. Поскольку его деятельность испытывает на себе воздействие различных внешних и внутренних помех, показатели эффективности работы предприятия отклоняются от расчетной траектории. Ввиду этого методы статистической динамики оптимизируют принятый критерий эффективности управления предприятием. Такими критериями могут быть средняя квадратическая погрешность, математическое ожидание или дисперсия возникающего отклонения показателя эффективности, вероятность невыхода этого отклонения за пределы заданных границ и др.11
Задачи разработки решений в условиях неопределенности примыкают к игровым и отличаются от них тем, что поведение "конфликтующих" сторон меняется с течением времени. Поскольку эволюция состояний этих сторон описывается дифференциальными уравнениями, раздел математики, анализирующий процесс принятия решений для "движущихся" систем, получил название теории дифференциальных игр.
Примером такой игры может служить задача о преследовании одного управляемого объекта другим12. Изменяя свое поведение во времени, эти объекты стремятся достичь противоположных целей: первый намерен как можно быстрее встретиться со вторым, а тот наоборот - избежать или хотя бы максимально отсрочить момент встречи. Задача состоит в том, чтобы, зная законы движения, ресурсы и текущее состояние этих объектов, выбрать такую стратегию поведения, которая обеспечила бы встречу объектов в минимальный срок.
По-видимому, аналогичная картина складывается и в ходе конкурентной борьбы предприятий, когда одно из них ставит своей целью приблизиться по тем или иным показателям к уровню лидирующего предприятия. Среди таких показателей - конкурентоспособность продукции или услуги, занимаемая предприятием доля рынка, доходность или прибыльность его деятельности и др.
При решении динамических задач в условиях риска и неопределенности, как и статических задач подобного рода, могут быть полезны эвристические методы, восполняющие дефицит информации о среде предприятия.
Подводя черту, следует заметить, что в настоящее время динамические задачи по степени разработки и применения в практике работы управленческого персонала предприятий уступают статическим.
Развитие современных методов поиска управленческих решений основывается на продвижении возможностей математического моделирования и на рациональном сочетании формализованных и неформализованных приемов в человеко-машинных компьютерных процедурах.
| 1 Кравченко Л.И. Анализ хозяйственной деятельности предприятий общественного питания. М.: Финансы, учет, аудит, 1998. |
| 2 Хаксевер К., Рендер Б., Рассел Р., Мердик Р. Управление и организация в сфере услуг / пер. с англ. 2-е изд. СПб.: Питер, 2002. |
| 3 Курицкий Б.Я. Оптимизация вокруг нас. Л.: Машиностроение. Ленингр. отделение, 1989. |
| 4 Курицкий Б.Я. Оптимизация вокруг нас. Л.: Машиностроение. Ленингр. отделение, 1989. |
| 5 Курицкий Б.Я. Оптимизация вокруг нас. Л.: Машиностроение. Ленингр. отделение, 1989. |
| 6 См. их сводку, например, в "Системный анализ в экономике и организации производства" / под общ. ред. С.А. Валуева, В.Н. Волковой. Л.: Политехника, 1991. С. 85-97. |
| 7 См. Андрейчиков А.В., Андрейчикова О.Н. Анализ, синтез, планирование решений в экономике. М.: Финансы и статистика, 2000. |
| 8 Беллман Р., Заде Л. Принятие решений в расплывчатых условиях // Вопросы анализа и процедуры принятия решений. М.: Мир, 1976. Заде Л.А. Основы нового подхода к анализу сложных систем и процессов принятия решений // Математика сегодня. М.: Знание, 1974. |
| 9 Обработка нечеткой информации в системах принятия решений / Сост. А.Н. Борисов, А.В. Алексеев, Г.В. Меркурьева и др. М.: Радио и связь, 1989. С. 16-17. |
| 10 Беллман Р., Заде Л. Принятие решений в расплывчатых условиях // Вопросы анализа и процедуры принятия решений. М.: Мир, 1976. |
| 11 Энциклопедия кибернетики: В 2 т. Киев: Гл. ред. УСЭ, 1975. Т. 2 / отв. ред. В.М. Глушков. С. 333-335. |
| 12 Математика и кибернетика в экономике. Словарь-справочник / отв. ред. Н.П. Федоренко. 3-е изд., перераб. и доп. М.: Экономика, 1975. С. 119-120. |