|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Алгоритмы нечеткого контроля и управления
Многошаговые процессы принятия решений
Для простоты будем полагать, что управляемая система  является инвариантной
по времени детерминированной системой с конечным числом состояний.
Именно каждое состояние
является инвариантной
по времени детерминированной системой с конечным числом состояний.
Именно каждое состояние 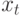 , в котором система
, в котором система  находится в момент
времени
находится в момент
времени  ,
, 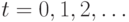 , принадлежит заданному
конечному множеству
возможных состояний
, принадлежит заданному
конечному множеству
возможных состояний 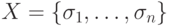 ; при этом
входной
сигнал в момент времени
; при этом
входной
сигнал в момент времени  является элементом множества
является элементом множества  .
Динамика системы во времени описывается уравнением состояния
.
Динамика системы во времени описывается уравнением состояния

 — заданная функция, отображающая
— заданная функция, отображающая  в
в  .
Таким образом,
.
Таким образом,  представляет собой последующее
состояние для
представляет собой последующее
состояние для 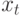 при входном сигнале
при входном сигнале 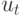 .
Считается также,
что заданы начальное состояние
.
Считается также,
что заданы начальное состояние 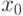 и фиксированное время
окончания
процесса
и фиксированное время
окончания
процесса  .
.Предполагается, что в каждый момент времени  на входную
переменную
наложено нечеткое ограничение
на входную
переменную
наложено нечеткое ограничение 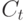 , являющееся нечетким
множеством в
, являющееся нечетким
множеством в  с функцией
принадлежности
с функцией
принадлежности 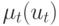 . Кроме того, считается, что цель —
нечеткое множество
. Кроме того, считается, что цель —
нечеткое множество 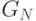 в
в  , определяемое функцией
принадлежности
, определяемое функцией
принадлежности 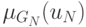 . Задача заключается в нахождении
максимизирующего решения.
. Задача заключается в нахождении
максимизирующего решения.
Можно записать решение как нечеткое множество в 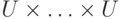 в виде
в виде
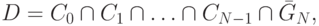
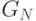 — нечеткое множество в
— нечеткое множество в 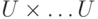 , индуцируемое
, индуцируемое 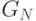 в
в  .
Для функции принадлежности имеем
.
Для функции принадлежности имеем
где  может быть выражено как функция от
может быть выражено как функция от 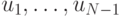 и
и 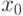 путем последовательного применения уравнения
путем последовательного применения уравнения 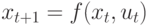 .
.
Для многошаговых процессов целесообразно представить решение в виде:
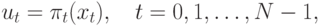
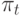 — принятая "стратегия", или
правило выбора входного
воздействия
— принятая "стратегия", или
правило выбора входного
воздействия 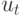 в зависимости от состояния системы
в зависимости от состояния системы 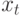 .
.Таким образом, задача сводится к нахождению оптимальных стратегий 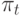 и соответствующей
последовательности входных воздействий
и соответствующей
последовательности входных воздействий 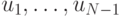 ,
максимизирующих
,
максимизирующих  . Для решения применяется метод
динамического программирования:
. Для решения применяется метод
динамического программирования:
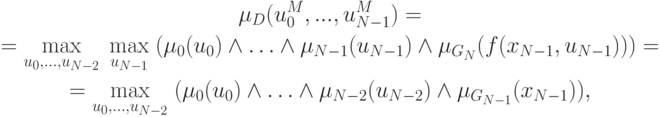
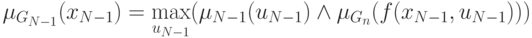 может рассматриваться как функция принадлежности нечеткой цели в момент
может рассматриваться как функция принадлежности нечеткой цели в момент 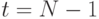 ,
индуцированной заданной целью
,
индуцированной заданной целью 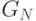 в момент
в момент 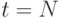 .
.Повторяя процесс обратных итераций, получаем систему рекуррентных уравнений

 ,
которая
дает решение задачи. Таким образом, максимизирующее решение достигается
последовательной максимизацией величин
,
которая
дает решение задачи. Таким образом, максимизирующее решение достигается
последовательной максимизацией величин 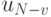 , причем
, причем  определяется как функция от
определяется как функция от  .
.В качестве простого примера рассмотрим систему с тремя
состояниями 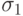 ,
, 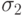 и
и  и двумя входными
сигналами
и двумя входными
сигналами 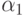 и
и 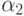 . Пусть
. Пусть 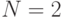 и нечеткая цель в момент
времени
и нечеткая цель в момент
времени 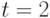 определяется функцией принадлежности, принимающей
значения
определяется функцией принадлежности, принимающей
значения

Пусть далее, нечеткие ограничения в моменты 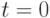 и
и 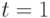 задаются функциями
задаются функциями

Допустим, что таблица изменения состояний, задающая функцию  ,
имеет следующий вид:
,
имеет следующий вид:
Находим функцию принадлежности нечеткой цели в момент 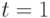 :
:

Соответствующее максимизирующее решение имеет вид:
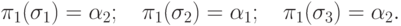
Аналогично, для  имеем
имеем

Итак, если начальное состояние в момент времени 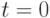 есть
есть 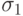 , то максимизирующим
решением будет
, то максимизирующим
решением будет 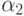 , причем соответствующее значение функции
принадлежности
, причем соответствующее значение функции
принадлежности 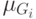 равно 0,8.
равно 0,8.
