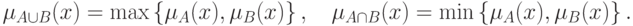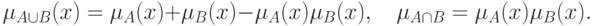|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие множества как способы формализации нечеткости
Для определения пересечения и объединения нечетких множеств наибольшей популярностью пользуются следующие три группы операций:
Дополнение нечеткого множества во всех трех случаях определяется одинаково:  .
.
Пример.
Пусть  — нечеткое множество "от 5 до 8" (рис.1.3а) и
— нечеткое множество "от 5 до 8" (рис.1.3а) и  —
нечеткое множество "около 4" (рис.1.3б), заданные своими
функциями принадлежности:
—
нечеткое множество "около 4" (рис.1.3б), заданные своими
функциями принадлежности:
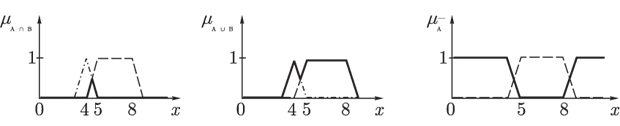
Тогда, используя максиминные операции, мы получим множества, изображенные на рис.1.4.
Заметим, что при максиминном и алгебраическом определении операций не будут выполняться
законы противоречия и исключения третьего  ,
а в случае ограниченных операций не будут выполняться свойства идемпотентности
,
а в случае ограниченных операций не будут выполняться свойства идемпотентности 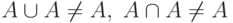 и дистрибутивности:
и дистрибутивности:

Можно показать, что при любом построении операций объединения и пересечения в теории нечетких множеств приходится отбрасывать либо законы противоречия и исключения третьего, либо законы идемпотентности и дистрибутивности.
Носителем нечеткого множества  называется четкое множество
называется четкое множество 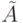 таких точек в
таких точек в  , для которых величина
, для которых величина  положительна,
т.е.
положительна,
т.е.  .
.
Высотой нечеткого множества  называется величина
называется величина 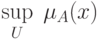 .
.
Нечеткое множество  называется нормальным,
если
называется нормальным,
если  . В противном случае оно
называется субнормальным.
. В противном случае оно
называется субнормальным.
Нечеткое множество называется пустым,
если 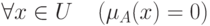 . Очевидно, что в данном
универсуме
. Очевидно, что в данном
универсуме  существует единственное пустое нечеткое множество. Непустое
субнормальное нечеткое множество можно привести к нормальному (нормализовать)
по формуле
существует единственное пустое нечеткое множество. Непустое
субнормальное нечеткое множество можно привести к нормальному (нормализовать)
по формуле
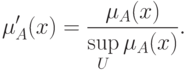
Множеством уровня  (
(  - срезом ) нечеткого множества
- срезом ) нечеткого множества  называется четкое подмножество универсального множества
называется четкое подмножество универсального множества  , определяемое по формуле
, определяемое по формуле
![A_\alpha = \left\{ {x|\mu _A (x) \geqslant \alpha } \right\}
, \quad\t{где}\quad
\alpha \in \left[ {0,1} \right]
.](/sites/default/files/tex_cache/ed4f16cb82784acb14383e30beee56f2.png)
Множество строгого уровня
определяется в виде 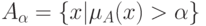 . В частности,
носителем нечеткого множества является множество элементов, для
которых
. В частности,
носителем нечеткого множества является множество элементов, для
которых 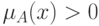 . Понятие множества уровня является расширением
понятия интервала. Оно представляет собой объединение не более чем счетного числа интервалов. Соответственно, алгебра интервалов есть частный случай алгебры множеств уровня.
. Понятие множества уровня является расширением
понятия интервала. Оно представляет собой объединение не более чем счетного числа интервалов. Соответственно, алгебра интервалов есть частный случай алгебры множеств уровня.
Точка перехода нечеткого множества  — это такой элемент
— это такой элемент 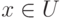 , для которого
, для которого 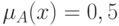 .
.
Четкое множество  , ближайшее к нечеткому множеству
, ближайшее к нечеткому множеству  , определяется
следующим образом:
, определяется
следующим образом:
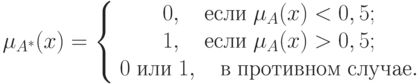
Нечеткое множество  в пространстве
в пространстве 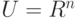 называется выпуклым
нечетким множеством тогда и только тогда, если его функция принадлежности
выпукла, т.е. для каждой пары точек
называется выпуклым
нечетким множеством тогда и только тогда, если его функция принадлежности
выпукла, т.е. для каждой пары точек  и
и  из
из  функция принадлежности
удовлетворяет неравенству
функция принадлежности
удовлетворяет неравенству 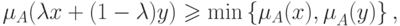 для любого
для любого ![\lambda \in \left[ {0,1} \right]](/sites/default/files/tex_cache/da7ee0f038c28b0151268127ce03a358.png) .
.