НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 8: Линейные подпространства линейных пространств

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 10.09.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать программу

Решетка подпространств линейного пространства

Рассмотрим частично упорядоченное множество всех линейных подпространств U линейного пространства _K V:

$L({}_K V) = \{U\mid U\subseteq {}_K V\},$

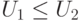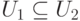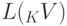где $U_1 \leq U_2$ означает $U_1\subseteq U_2$ . Для любых двух элементов $U_1,U_2\in L({}_K V)$ существует точная верхняя грань $U_1\vee U_2=U_1+U_2$ и точная нижняя грань $U_1\wedge U_2=U_1\cap U_2$ , таким образом, частично упорядоченное множество $L({}_K V)$ является решеткой линейного пространства _K V ), при этом 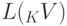$L({}_K V)$ - решетка с дополнениями (т. е. для всякого 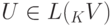$U\in L({}_K V)$ существует такой элемент $W\in L({}_K V)$ , что $U\vee W=V$ , $U\wedge W=\{0\}$ ).

Теорема 9.14.1. В решетке 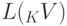$L({}_K V)$ выполнено следующее модулярное тождество Дедекинда: если 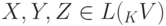$X,Y,Z\in L({}_K V)$ , $X\subseteq Z$ , то

$X+(Y\cap Z) = (X+Y)\cap Z.$

Доказательство.

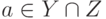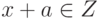1) Пусть $x+a\in X+(Y\cap Z)$ , где $x\in X$ , $a\in Y\cap Z$ , тогда $a\in Y$ , и поэтому $x+a\in X+Y$ ; $x\in X\subseteq Z$ , $a\in Y\cap Z\subseteq Z$ , и следовательно, $x+a\in Z$ ; итак, $x+a\in (X+Y)\cap Z$ .
2) Пусть $z\in (X+Y)\cap Z$ , z=x+y, где $x\in X$ , $y\in Y$ . Тогда $y=z-x\in Y\cap Z$ , поскольку $X\subseteq Z$ , и поэтому $z=x+y\in X+(Y\cap Z)$ .

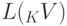Замечание 9.14.2. Если $\dim {}_K V \geq 2$ , то в $L({}_K V)$ не выполняется тождество дистрибутивности

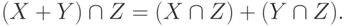
$(X+Y)\cap Z=(X\cap Z)+(Y\cap Z).$

Действительно, в _K V=K² имеем для

$\begin{gathe} X+Y={}_K V=K^2,\quad X\cap Z=\{0\},\quad Y\cap Z=\{0\},\\ (X+Y)\cap Z=Z\neq \{0\} = (X\cap Z)+(Y\cap Z). \end{gathe}$

Замечание 9.14.3. Итак, мы убедились в том, что решетка 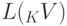$L({}_K V)$ всех линейных подпространств линейного пространства _K V является модулярной (дедекиндовой) решеткой с дополнениями.

Дальше >>

Алгебра матриц и линейные пространства

Алгебра матриц и линейные пространства

Линейные подпространства линейных пространств

Решетка подпространств линейного пространства

Вопросы и ответы

Студенты

Авторизоваться

Алгебра матриц и линейные пространства

Алгебра матриц и линейные пространства

Линейные подпространства линейных пространств

Решетка подпространств линейного пространства

Вопросы и ответы

Студенты