НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 5: Многочлены от матриц, теорема Гамильтона-Кэли. Обратная матрица

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 10.09.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать программу

Обратная матрица

Определение 8.7.1. Пусть 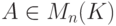$A\in M_n(K)$ - квадратная матрица. Будем говорить, что матрица 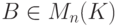$B\in M_n(K)$ является обратной к A, если AB=E=BA .

Замечание 8.7.2 (для любой ассоциативной операции). Если обратная матрица B к матрице A существует, то она однозначно определена. Действительно, пусть AB=E=BA и AC=E=CA, тогда C=EC=(BA)C=B(AC)=BE=B (это повтор того, что мы уже отмечали ранее: единственность обратного элемента, если он существует, для любого элемента моноида). В этом случае однозначно определенную обратную матрицу B мы будем обозначать через A^-1 : AA^-1=E=A^-1A.

Теорема 8.7.3 (об обратной матрице). Пусть 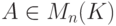$A\in M_n(K)$ - квадратная $(n\times n)$ -матрица. Тогда:

обратная матрица B = (b_ij) = A^-1 существует тогда и только тогда, когда $|A|\neq 0$ ;
в этом случае $b_{ij}=\smash{\frac{A_{ji}}{|A|}}$ (формула для элемента обратной матрицы);
$|A^{-1}|=\smash[t]{\frac{1}{|A|}}$ .

Доказательство.

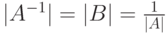а) Если AB=E, то 1=|E|=|AB|=|A|,|B|, поэтому $|A|\neq 0$ и, более того, $|A^{-1}|=|B|=\frac{1}{|A|}$ .

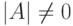б) Если $|A|\neq 0$ , то рассмотрим B=(b_ij), где 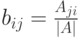$b_{ij}=\frac{A_{ji}}{|A|}$ . Ясно, что AB=E=BA (принимая во внимание разложение определителя по строкам и столбцам, а также "фальшивое" разложение), т. е. B=A^-1.

Следствие 8.7.4. Если $A,B\in M_n(K)$ , то из AB=E следует, что BA=E (матрица, имеющая правую обратную, обратима (двусторонне)).

Доказательство. Если AB=E, то |A|,|B|=|AB|=|E|=1, поэтому 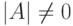$|A|\neq 0$ , но тогда существует двусторонняя обратная матрица A^-1. Таким образом, 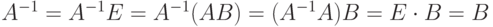$A^{-1}=A^{-1}E=A^{-1}(AB)=(A^{-1}A)B=E\cdot B=B$ , следовательно, BA=A^-1A=E.

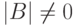Следствие 8.7.5. Для $A,B\in M_n(K)$ имеем |AB|=|A|,|B|, поэтому $|AB|\neq 0$ тогда и только тогда, когда $|A|\neq 0$ и $|B|\neq 0$ , т. е. обратная матрица (AB)^{-1} существует тогда и только тогда, когда существуют A^-1 и B^-1. Более того, в этом случае (AB)^-1=B^-1A^-1.

Доказательство. (AB)(B^-1A^-1)=E=(B^-1A^-1)(AB).

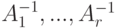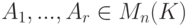Следствие 8.7.6. Если существуют обратные матрицы $A^{-1}_1,...,\allowbreak A^{-1}_r$ для $A_1,...,A_r\in M_n(K)$ , то $(A_1A_2\cdot...\cdot A_r)^{-1}= A^{-1}_r\cdot...\cdot A^{-1}_2A^{-1}_1$ .

Следствие 8.7.7. Если существует обратная матрица A^-1 для 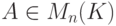$A\in M_n(K)$ , то (A^-1)^-1=A.

Доказательство. A^-1A=E=A A^-1 (с точки зрения матрицы A^-1 : A=(A^-1)^-1 ).

Упражнение 8.7.8. Пусть

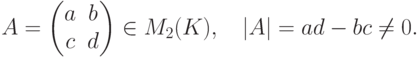
$A= \begin{pmatrix} a & b\\ c & d \end{pmatrix} \in M_{2}(K),\quad |A|=ad-bc\neq 0.$

Тогда:

$\begin{gathe} B = (b_{ij}=A_{ji}) = \begin{pmatrix} \phm d & -b\\ -c & \phm a \end{pmatrix};\\ A^{-1} = \begin{pmatrix} \phm \frac{d}{ad-bc} & -\frac{b}{ad-bc}\\[3\jot] -\frac{c}{ad-bc} & \phm \frac{a}{ad-bc} \end{pmatrix}. \end{gathe}$

Упражнение 8.7.9. Пусть

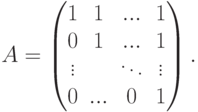
$A = \begin{pmatrix} 1 & 1 & ... & 1\\ 0 & 1 & ... & 1\\ \vdots & & \ddots & \vdots\\ 0 & ... & 0 & 1 \end{pmatrix}.$

Тогда

$A^{-1} = \begin{pmatrix} 1 & -1 & & \lefteqn{\raisebox{-5pt}[0pt][0pt]{\text{\hspace*{-10pt}\Large 0 }}}\\ & \ddots & \ddots \\ & & \ddots & -1\\ \lefteqn{\raisebox{5pt}[0pt][0pt]{\text{\hspace*{5pt}\Large 0 }}} & & & 1 \end{pmatrix}.$

Упражнение 8.7.10. Найти

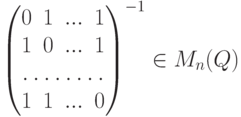
$\begin{pmatrix} 0 & 1 & ... & 1\\ 1 & 0 & ... & 1\\ \hdotsfor{4}\\ 1 & 1 & ... & 0 \end{pmatrix}^{-1} \in M_n( Q)$

(матрица размера $n\times n$ , на главной диагонали которой стоят нули, а все остальные элементы равны 1 ).

Упражнение 8.7.11. Пусть

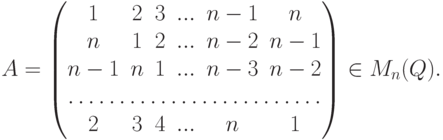
$A = \begin{pmatrix} 1 & 2 & 3 & ... & n-1 & n\\ n & 1 & 2 & ... & n-2 & n-1\\ n-1 & n & 1 & ... & n-3 & n-2\\ \hdotsfor{6}\\ 2 & 3 & 4 & ... & n & 1 \end{pmatrix} \in M_n( Q).$

Тогда

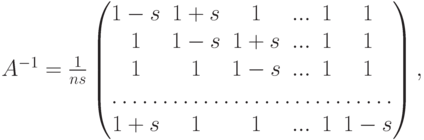
$A^{-1} = \frac{1}{ns} \begin{pmatrix} 1-s & 1+s & 1 & ... & 1 & 1\\ 1 & 1-s & 1+s & ... & 1 & 1\\ 1 & 1 & 1-s & ... & 1 & 1\\ \hdotsfor{6}\\ 1+s & 1 & 1 & ... & 1 & 1-s \end{pmatrix},$

где $s=\frac{n(n+1)}{2}$ .

Теорема 8.7.12 (о линейных группах).

а) Множество обратимых матриц

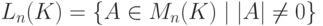
$L_n(K)=\{A\in M_n(K) \mid |A|\neq 0\}$

с операцией умножения является группой ( линейная группа ).

б) Множество матриц с единичным определителем

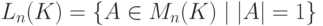
$L_n(K)=\{A\in M_n(K) \mid |A|=1\}$

с операцией умножения является группой ( специальная линейная группа ).

Доказательство.

а) Все проверки для 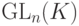$\GL_n(K)$ уже были проведены.

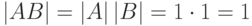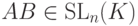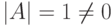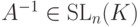б) Если $A,B\in \SL_n(K)$ , то |A|=1, |B|=1, поэтому $|AB|=|A|\,|B|=1\cdot 1=1$ , следовательно, $AB\in \SL_n(K)$ . Ясно, что |E|=1, т. е. $E\in \SL_n(K)$ . Если $A\in \SL_n(K)$ , то $|A|=1\neq 0$ , т. е. существует A^-1, при этом $|A^{-1}|=\frac{1}{|A|}=1$ , поэтому $A^{-1}\in \SL_n(K)$ .

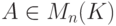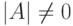Лемма 8.7.13. Если $A\in \GL_n(K)$ (т. е. $A\in M_n(K)$ и $|A|\neq 0$ ), то $|A^*|=|A|\neq 0$ (т. е. $A^*\in\GL_n(K)$ ) и, более того, (A^*)^-1=(A^-1)^*.

Доказательство.

$\begin{align*} (A^{-1})^*A^* &= (AA^{-1})^*=E^*=E;\\ A^*(A^{-1})^* &= (A^{-1}A)^*=E^*=E \end{align*}$

(с точки зрения матрицы A^* : (A^*)^-1=(A^-1)^* ).

Определение 8.7.14. Квадратная матрица 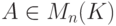$A\in M_n(K)$ называется ортогональной матрицей, если A^-1=A^* .

Теорема 8.7.15. Совокупность ортогональных матриц $O_n(K)=\{A\in M_n(K) \mid A^{-1}=A^*\}$ относительно умножения матриц является группой.

Доказательство.

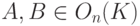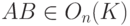а) Если $A,B\in O_n(K)$ , то A^-1=A^* и B^-1=B^*. Тогда (AB)^-1=B^-1A^-1=B^*A^*=(AB)^*, поэтому $AB\in O_n(K)$ .

б) E^-1=E=E^*, т. е. 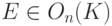$E\in O_n(K)$ .

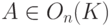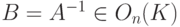в) Если $A\in O_n(K)$ , то для B=A^-1 имеем B^-1=(A^-1)^-1=(A^*)^-1=(A^-1)^*=B^*, следовательно, $B=A^{-1}\in O_n(K)$ .

Задача 8.7.16. Пусть 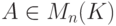$A\in M_n(K)$ и существует такое число k, что A^k - нулевая матрица. Покажите, что матрицы E-A, E+A обратимы (здесь E - единичная матрица в M_n(K) ).

Задача 8.7.17. Для $A,B\in M_n(K)$ равносильны условия:

матрица E-AB обратима;
матрица E-BA обратима

(этот факт полезен при построении теории определителей над произвольным кольцом R : в алгебраической K -теории - функтор K_1(R) ).

Более того, можно доказать, что если 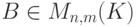$A\in M_{m,n}(K)$ , $B\in M_{n,m}(K)$ , то E_m-AB - обратимая матрица тогда и только тогда, когда E_n-BA - обратимая матрица.

Задача 8.7.18. Найти число элементов в группах 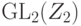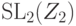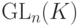$\GL_2( Z_2)$ , $\SL_2( Z_2)$ , $\GL_n(K)$ , где K - конечное поле из q элементов.

Упражнение 8.7.19. Рассмотрим отображение

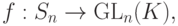
$f: S_n\to\GL_n(K),$

где

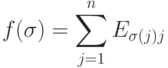
$f(\sigma)=\sum_{j=1}^{n} E_{\sigma(j)j}$

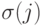(т. е. в j -м столбце единственная единица стоит в $\sigma(j)$ -й строке, остальные элементы нулевые). Тогда

$|f(\sigma)|=\varepsilon(\sigma)= \begin{cases} 1, & \sigma\in\mA_n,\\ -1 & \sigma\in S_n\setminus\m A_n, \end{cases}$

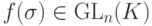поэтому $f(\sigma)\in\GL_n(K)$ . Покажите, что f - инъективный гомоморфизм (т. е. группа 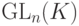$\GL_n(K)$ содержит подгруппу, изоморфную группе S_n ).

Действительно, для 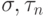$\sigma,\tau\inS_n$ имеем

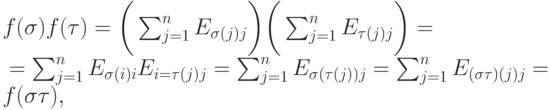
$\begin{mult} f(\sigma)f(\tau)= \biggl(\,\sum_{j=1}^{n}E_{\sigma(j)j}\biggr) \biggl(\,\sum_{j=1}^{n}E_{\tau(j)j}\biggr)={} \\ {}=\sum_{j=1}^{n}E_{\sigma(i)i}E_{i=\tau(j)j}= \sum_{j=1}^{n}E_{\sigma(\tau(j))j}=\sum_{j=1}^{n}E_{(\sigma\tau)(j)j}= f(\sigma\tau), \end{mult}$

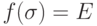т. е. f - гомоморфизм. Если $f(\sigma)=E$ , то

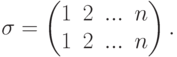
$\sigma= \begin{pmatrix} 1 & 2 & ... & n\\ 1 & 2 & ... & n \end{pmatrix}.$

Итак, f - инъективный гомоморфизм.

Контрольные вопросы 8.7.20.

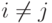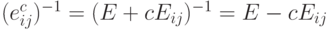$i\ne j$ , $(e_{ij}^c)^{-1}=(E+cE_{ij})^{-1}=E-cE_{ij}$ ;
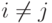$i\ne j$ , $t_{ij}^{-1}=t_{ij}$ ;
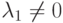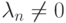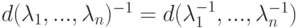$\lambda_1\neq 0$ ,..., $\lambda_n\neq 0$ , $d(\lambda_1,...,\lambda_n)^{-1}= d(\lambda_1^{-1},...,\lambda_n^{-1})$ .