Опубликован: 10.09.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова
Лекция 4:
Линейное пространство M_m,n (K) прямоугольных матриц размера mxn
Ассоциативность произведения матриц
Теорема 8.4.1 (об ассоциативности произведения матриц). Пусть
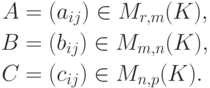
Первое доказательство. Пусть
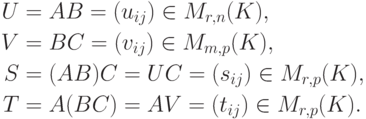


Второе доказательство. Пусть в диаграмме

 . Вычисляя матрицу этого линейного преобразования (по теореме о матрице произведения линейных преобразований), получаем, что (AB)C=A(BC).
. Вычисляя матрицу этого линейного преобразования (по теореме о матрице произведения линейных преобразований), получаем, что (AB)C=A(BC).Следствие 8.4.2. Квадратные  -матрицы Mn(K) относительно операции умножения являются моноидом (т. е. операция умножения определена на Mn(K), ассоциативна и обладает нейтральным элементом E=En ).
-матрицы Mn(K) относительно операции умножения являются моноидом (т. е. операция умножения определена на Mn(K), ассоциативна и обладает нейтральным элементом E=En ).
Теорема 8.4.3 (о дистрибутивности для матриц). Пусть


Доказательство. Действительно, для любого места (i,j) имеем

Следствие 8.4.4. Для любых квадратных матриц 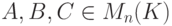 имеем
имеем


