НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 2: Вычисление определителей

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 10.09.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать программу

Определитель Вандермонда

Теорема 6.9.1.

$\begin{mult} \nota {V(a_1,...,a_n)} = \begin{vmatrix} 1 & a_1 & ... & a_1^{n-1}\\ 1 & a_2 & ... & a_2^{n-1}\\ \vdots & \vdots & & \vdots\\ 1 & a_n & ... & a_n^{n-1} \end{vmatrix} ={} \\ {}= \prod_{1 \leq j<i \leq n} (a_i-a_j),\quad a_1,...,a_n\in K. \end{mult}$

Доказательство. Проведем индукцию по n (начало индукции n=2 ). Пусть утверждение верно для n'<n. Тогда, применяя элементарные преобразования столбцов $\hat A_n-a_1\hat A_{n-1}$ , $\hat A_{n-1}-a_1\hat A_{n-2}$ ,..., $\hat A_2-a_1\hat A_1$ и предположение индукции, получаем

$\begin{align*} & V(a_1,...,a_n) = \begin{vmatrix} 1 & a_1 & ... & a_1^{n-1}\\ 1 & a_2 & ... & a_2^{n-1}\\ \vdots & \vdots & & \vdots\\ 1 & a_n & ... & a_n^{n-1} \end{vmatrix} ={} \\ & \quad {}= \begin{vmatrix} 1 & 0 & ... & 0\\ 1 & (a_2-a_1) & ... & a_2^{n-2}(a_2-a_1)\\ \vdots & \vdots & & \vdots\\ 1 & (a_n-a_1) & ... & a_n^{n-2}(a_n-a_1) \end{vmatrix} ={} \\ & \quad {}= \begin{vmatrix} (a_2-a_1) & ... & a_2^{n-2}(a_2-a_1)\\ \vdots & & \vdots\\ (a_n-a_1) & ... & a_n^{n-2}(a_n-a_1) \end{vmatrix} ={} \\ & \quad {}= (a_2-a_1)... (a_n-a_1) \begin{vmatrix} 1 & a_2 & ... & a_2^{n-2}\\ \vdots & \vdots & & \vdots\\ 1 & a_n & ... & a_n^{n-2} \end{vmatrix} ={} \\ & \quad {}= \prod_{k=2}^n (a_k-a_1) V(a_2,...,a_n) ={} \\ & \quad {}= \prod_{k=2}^n (a_k-a_1) \prod_{2 \leq j<i \leq n} (a_i-a_j)= \prod_{1 \leq j<i \leq n} (a_i-a_j). \end{align*}$

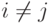Следствие 6.9.2. $V(a_1,...,a_n)\neq 0$ тогда и только тогда, когда $a_i\neq a_j$ при $i\neq j$ (т. е. когда все элементы a₁,a₂,...,a_n различны).

Теорема 6.9.3 (интерполяционная формула Лагранжа).

Если a₁,...,a_n - различные элементы поля K, b₁,...,b_n - любые элементы поля K, то существует и единственный многочлен $f(x)\in K[x]$ такой, что $\deg f(x) \leq n-1$ и f(a_i)=b_i для всех $1 \leq i \leq n$ (здесь $\deg f(x)$ - степень многочлена f(x) ).
Этот многочлен имеет вид
$f(x)=\sum_{i=1}^{n} b_i \frac{(x-a_1)... \widehat{(x-a_i)}... (x-a_n)}% {(a_i-a_1)... \widehat{(a_i-a_i)}... (a_i-a_n)}$
(здесь $\widehat{(x-a_i)}$ , $\widehat{(a_i-a_i)}$ означает, что эти множители не входят в произведения).
Интерполяционный многочлен $f(x)\in K[x]$ , $\deg f(x)\pleq n-1$ , для которого f(a_i)=b_i, i=1,...,n, можно находить методом Ньютона в виде
$\begingroup \setlength{\multlinegap}{0pt} \begin{mult} f(x)={} \\ {}=\lambda_0 +\lambda_1 (x-a_1)+\lambda_2 (x-a_1)(x-a_2)+...+ \lambda_{n-1} \smash[t]{\prod_{i=1}^{n-1} (x-a_i)}, \end{mult} \endgroup%$
при этом коэффициенты определяются последовательно: при x=a_1 имеем $b_1=f(a_1)=\lambda_0$ , т. е. $\lambda_0=b_1$ ; при x=a₂ имеем $b_2=f(a_2)=b_1+\lambda_1(a_2-a_1)$ , т. е. $\lambda_1=(b_2-b_1)/(a_2-a_1)$ ;...; при x=a_n-1 получаем
$b_{n-1}=\lambda_0+\lambda_1(a_{n-1}-a_1)+...+ \lambda_{n-2}\prod\limits_{i=1}^{n-2}(a_{n-1}-a_i)$
и находим $\lambda_{n-2}$ (коэффициент при $\lambda_{n-2}$ отличен от нуля); полагая x=a_n, имеем коэффициент $\smash[b]{\prod\limits_{i=1}^{n-1}} (a_n-a_i)\neq 0$ при $\lambda_{n-1}$ в равенстве
$b_n=\lambda_0+\lambda_1(a_n-a_1)+...+ \lambda_{n-1}\prod\limits_{i=1}^{n-1}(a_n-a_i)$
и находим $\lambda_{n-1}$ .

Доказательство.

Будем искать многочлен f(x)=f₀+f₁x+...+f_n-1x^n-1, где f₀,f₁,...,f_n-1 - неизвестные коэффициенты (элементы поля K ), такой, что
$\begin{align*} & f(a_1)=f_0+f_1a_1+...+f_{n-1}a_1^{n-1}=b_1,\\ & \quad\vdots\\ & f(a_n)=f_0+f_1a_n+...+f_{n-1}a_n^{n-1}=b_n. \end{align*}$
Определитель этой системы
$V(a_1,...,a_n)= \begin{vmatrix} 1 & a_1 & ... & a_1^{n-1} \\ \vdots & \vdots && \vdots \\ 1 & a_n & ... & a_n^{n-1} \end{vmatrix} = \prod_{1 \leq j<i \leq n} (a_i-a_j)\neq 0,$
поскольку все элементы a₁,...,a_n различны. Поэтому такой многочлен f(x) существует (и единственный).
Очевидно, что приведенный многочлен в форме Лагранжа
$f(x)=\sum_{i=1}^{n} b_i \frac{(x-a_1)... \widehat{(x-a_i)}... (x-a_n)}% {(a_i-a_1)... \widehat{(a_i-a_i)}... (a_i-a_n)}$
удовлетворяет двум условиям:
$\begin{align*} & \deg f(x) \leq n-1;\\* & f(a_i)=b_i,\quad i=1,2,...,n. \end{align*}$
Многочлен f(x) в форме Ньютона удовлетворяет двум условиям:
$\begin{align*} & \deg f(x) \leq n-1;\\ & f(a_i)=b_i,\quad i=1,2,...,n. \end{align*}$