Аксиоматика теории вероятностей

Свойство 3. Всякая -алгебра является алгеброй.

Доказательство. Пусть 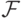- -алгебра. Нужно проверить, что она удовлетворяет свойству (A3), т.е. для любых 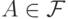и 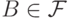выполняется .

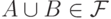Превратим пару в счетную последовательность событий так: 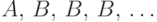, т.е. положим 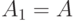, 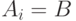при всех 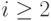. Объединение 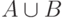совпадает с объединением всех множеств из этой бесконечной последовательности. А так как 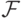- -алгебра, то

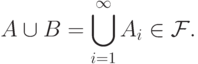
Итак, всякая -алгебра автоматически является алгеброй, но не наоборот. Приведем пример алгебры, не являющейся -алгеброй.

Пример 23. Пусть 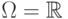, и пусть 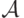- множество, содержащее любые конечные подмножества (т.е. состоящие из конечного числа точек, в том числе пустое) и их дополнения. Так, множество 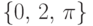принадлежит 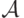, множество не принадлежит .

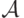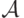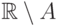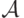Легко проверить, что множество является алгеброй. Действительно, пустое множество и само там содержатся, дополнение к любому конечному подмножеству множества вещественных чисел содержится в по определению, дополнение к множеству вида для конечных совпадает с и также принадлежит по определению. Свойство (A3) проверяется непосредственно: объединение любых конечных множеств снова конечно и поэтому принадлежит 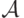. Объединение конечного множества с множеством вида 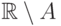, где конечно, есть снова множество вида , где конечно (или пусто) и т.д.

Однако алгебра 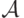не содержит ни одного счетного множества точек. Действительно, объединяя конечные множества в конечном числе, мы можем получить только конечное множество. Например, натуральный ряд 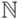не принадлежит 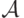. Поэтому 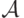не является -алгеброй: для бесконечной, но счетной последовательности одноточечных множеств из 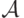их объединение 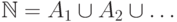не принадлежит .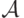

Все алгебры из примера 22 являются -алгебрами, поскольку содержат лишь конечное число элементов. Вообще, на конечном множестве понятия алгебры и -алгебры совпадают. Множество всех подмножеств является -алгеброй для любого .

Борелевская -алгебра. Приведем еще один пример -алгебры, которая нам будет необходима в дальнейшем,- -алгебры борелевских множеств на вещественной прямой.

Борелевской сигма-алгеброй в называется самая маленькая среди всех возможных -алгебр, содержащих любые интервалы на прямой. Разумеется, -алгебры, содержащие все интервалы, существуют. Например, множество всех подмножеств - это -алгебра, и она содержит все интервалы. Что же такое "самая маленькая -алгебра" из нескольких данных? Обратимся к примерам.

Пусть 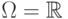- вещественная прямая. Рассмотрим некоторые наборы множеств, не являющиеся -алгебрами, и увидим, как их можно дополнить до -алгебр.

Пример 24. Множество не является -алгеброй, так как, например, . Самый маленький набор множеств, содержащий и являющийся -алгеброй (минимальная -алгебра), получится, если включить в него всевозможные объединения, пересечения и дополнения множеств из :

Определение 6. Минимальной -алгеброй, содержащей набор множеств , называется пересечение всех -алгебр, содержащих .

Еще раз напомним, что пересекать в определении 6 есть что: хотя бы одна -алгебра, содержащая данный набор множеств, всегда найдется - это -алгебра всех подмножеств .

Упражнение. Доказать, что пересечение двух -алгебр, содержащих набор множеств , снова является -алгеброй, содержащей .

Упражнение. Найти минимальную -алгебру, содержащую следующий набор подмножеств : .

Дадим определение борелевской сигма-алгебры. Пусть по-прежнему 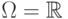, а множество состоит из всевозможных открытых интервалов 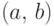, где : . Это множество всех интервалов не является ни алгеброй, ни -алгеброй.

Определение 7. Минимальная -алгебра, содержащая множество всех интервалов на вещественной прямой, называется борелевской -алгеброй в и обозначается .

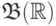Перечислим некоторые множества на прямой, содержащиеся в 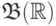по определению. Таковы все привычные нам множества. Чтобы получить множество, не содержащееся в 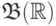, требуются специальные построения. Итак, мы знаем, что все интервалы на прямой принадлежат 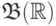, и 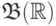- -алгебра. Отсюда сразу следует, что 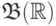содержит любое множество, которое можно получить из интервалов с помощью счетного числа операций объединения или пересечения, а также взятием дополнения.

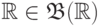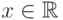В частности, по свойству (S1). Далее, все одноточечные множества , где , принадлежат 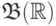. Действительно, интервалы 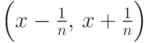принадлежат 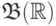, по определению, при любом . Их счетное пересечение также принадлежит 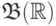по свойству (S4):

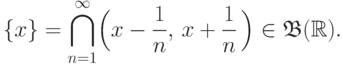
Далее, любой интервал вида (или , или ), где , принадлежит 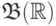как объединение открытого интервала и точки (или двух точек): .

Упражнение. Докажите, что множество натуральных чисел 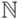и множество рациональных чисел принадлежат .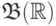

Борелевская -алгебра в 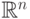строится совершенно так же, как в . Это должна быть минимальная -алгебра, содержащая все множества вида - уже не интервалы, как в , а прямоугольники в , параллелепипеды в 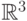и т.д. Вместе с ними 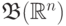содержит любые множества, являющиеся "предельными" для объединений измельчающихся прямоугольников. Например, круг в является борелевским множеством - можно изнутри или снаружи приблизить его объединениями прямоугольников.

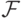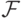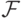Итак, мы определили специальный класс подмножеств , названный -алгеброй событий. Применение счетного числа любых операций (объединений, пересечений, дополнений) к множествам из снова дает множество из , т.е. не выводит за рамки этого класса. Событиями будем называть только множества .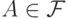

Определим теперь понятие вероятности как функции, определенной на множестве событий (функции, которая каждому событию ставит в соответствие число - вероятность этого события).