Основные семейства распределений
Примеры дискретных распределений
Вырожденное
распределение.
Говорят, что случайная величина  имеет вырожденное распределение в точке
имеет вырожденное распределение в точке 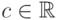 , и пишут:
, и пишут: 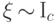 , если
, если  принимает
единственное значение
принимает
единственное значение  с вероятностью 1, т.е.
с вероятностью 1, т.е. 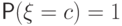 . Функция
распределения
. Функция
распределения  имеет вид
имеет вид
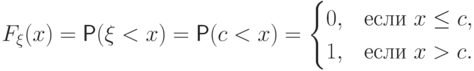
Распределение
Бернулли.
Говорят, что случайная величина  имеет распределение Бернулли с параметром
имеет распределение Бернулли с параметром  , и пишут:
, и пишут: 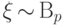 , если
, если  принимает значения
принимает значения  и
и  с вероятностями
с вероятностями  и
и 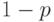 соответственно. Случайная величина
соответственно. Случайная величина  с таким распределением равна числу успехов
в одном испытании схемы Бернулли с вероятностью успеха
с таким распределением равна числу успехов
в одном испытании схемы Бернулли с вероятностью успеха  : ни
одного успеха или один успех.
Таблица распределения
: ни
одного успеха или один успех.
Таблица распределения  имеет вид:
имеет вид:
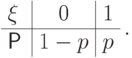
Функция распределения случайной величины  такова:
такова:

Биномиальное
распределение.
Говорят, что случайная величина  имеет биномиальное распределение с параметрами
имеет биномиальное распределение с параметрами 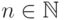 и
и 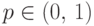 ,
и пишут:
,
и пишут: 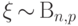 , если
, если  принимает значения
принимает значения 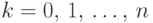 с вероятностями
с вероятностями 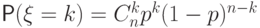 . Случайная
величина
с таким распределением имеет смысл числа успехов в
. Случайная
величина
с таким распределением имеет смысл числа успехов в  испытаниях
схемы Бернулли с вероятностью успеха
испытаниях
схемы Бернулли с вероятностью успеха  .
Таблица распределения
.
Таблица распределения  имеет вид
имеет вид

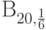 .
Распределение Бернулли совпадает с
распределением
.
Распределение Бернулли совпадает с
распределением 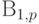 .
.Геометрическое
распределение.
Говорят, что случайная величина  имеет геометрическое распределение с параметром
имеет геометрическое распределение с параметром 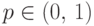 ,
и пишут
,
и пишут 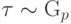 , если
, если  принимает значения
принимает значения 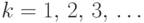 с вероятностями
с вероятностями 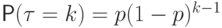 . Случайная величина
с таким распределением имеет смысл номера первого успешного испытания
в схеме Бернулли с вероятностью успеха
. Случайная величина
с таким распределением имеет смысл номера первого успешного испытания
в схеме Бернулли с вероятностью успеха  .
Таблица распределения
.
Таблица распределения  имеет вид
имеет вид
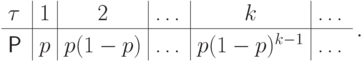
Распределение
Пуассона.
Говорят, что случайная величина  имеет распределение Пуассона с параметром
имеет распределение Пуассона с параметром 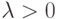 ,
и пишут:
,
и пишут: 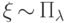 , если
, если  принимает значения
принимает значения 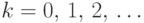 с вероятностями
с вероятностями 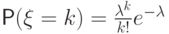 .
Таблицу распределения
.
Таблицу распределения  читатель может нарисовать
самостоятельно.
читатель может нарисовать
самостоятельно.
Распределение Пуассона возникло в теореме Пуассона
как предельное распределение для числа успехов в  испытаниях
схемы
Бернулли, когда число испытаний
испытаниях
схемы
Бернулли, когда число испытаний  увеличивается,
а вероятность успеха уменьшается обратно пропорционально
увеличивается,
а вероятность успеха уменьшается обратно пропорционально  .
Поэтому распределение Пуассона называют иначе распределением числа редких
событий.
.
Поэтому распределение Пуассона называют иначе распределением числа редких
событий.
Гипергеометрическое
распределение.
Говорят, что случайная величина  имеет гипергеометрическое распределение с параметрами
имеет гипергеометрическое распределение с параметрами  ,
,  и
и  ,
где
,
где 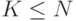 ,
,  ,
если
,
если  принимает целые значения
принимает целые значения  такие, что
такие, что 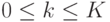 ,
, 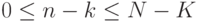 ,
с вероятностями
,
с вероятностями 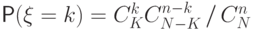 .
Случайная величина
с таким распределением имеет смысл числа белых шаров среди
.
Случайная величина
с таким распределением имеет смысл числа белых шаров среди  шаров, выбранных наудачу и без возвращения из урны, содержащей
шаров, выбранных наудачу и без возвращения из урны, содержащей  белых шаров и
белых шаров и  не белых.
не белых.
Упражнение. Построить графики функций распределения для вырожденного распределения, распределений Бернулли и Пуассона, биномиального и геометрического распределений.

