Схема Бернулли
Распределение числа успехов в n испытаниях
Определение 16. Схемой Бернулли называется последовательность независимых в совокупности
испытаний, в каждом из которых возможны лишь два исхода -
"успех"
и "неудача", при этом успех в одном испытании происходит
с вероятностью 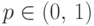 , а неудача - с вероятностью
, а неудача - с вероятностью 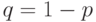 .
.
Под независимостью в совокупности
испытаний понимается независимость
в совокупности любых событий, относящихся к разным испытаниям. В испытаниях
схемы Бернулли,
когда с одним испытанием можно связать только два взаимоисключающих события,
независимость в совокупности испытаний означает, что при любом  независимы в совокупности
события
независимы в совокупности
события 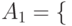 успех в первом испытании
успех в первом испытании 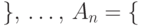 успех в
успех в  -м испытании
-м испытании 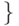 .
Эти события принадлежат одному и тому же
пространству элементарных исходов, полученному декартовым произведением
бесконечного числа двухэлементных множеств
.
Эти события принадлежат одному и тому же
пространству элементарных исходов, полученному декартовым произведением
бесконечного числа двухэлементных множеств 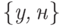 :
:

Обозначим через 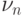 число успехов, случившихся в
число успехов, случившихся в  испытаниях схемы Бернулли.
Эта величина может принимать целые значения от нуля до
испытаниях схемы Бернулли.
Эта величина может принимать целые значения от нуля до  в зависимости от
результата
в зависимости от
результата  испытаний. Например, если все
испытаний. Например, если все  испытаний завершились неудачей,
то величина
испытаний завершились неудачей,
то величина 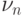 равна нулю.
равна нулю.
Теорема 13 (формула Бернулли).
При любом  имеет место равенство:
имеет место равенство:
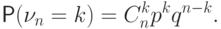
Доказательство.
Событие 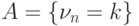 означает, что в
означает, что в  испытаниях
схемы Бернулли
произошло ровно
испытаниях
схемы Бернулли
произошло ровно  успехов.
Рассмотрим один из благоприятствующих событию
успехов.
Рассмотрим один из благоприятствующих событию  элементарных
исходов:
элементарных
исходов:

 испытаний завершились успехом,
остальные неудачей.
Поскольку испытания независимы, вероятность
такого элементарного исхода равна
испытаний завершились успехом,
остальные неудачей.
Поскольку испытания независимы, вероятность
такого элементарного исхода равна 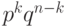 .
Другие благоприятствующие событию
.
Другие благоприятствующие событию  элементарные исходы отличаются лишь расположением
элементарные исходы отличаются лишь расположением  успехов на
успехов на  местах. Есть ровно
местах. Есть ровно 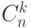 способов расположить
способов расположить  успехов на
успехов на  местах. Поэтому событие
местах. Поэтому событие  состоит из
состоит из 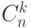 элементарных исходов, вероятность каждого из которых
также равна
элементарных исходов, вероятность каждого из которых
также равна 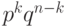 .
.Определение 17.
Набор чисел  называется биномиальным
распределением
вероятностей.
называется биномиальным
распределением
вероятностей.
Номер первого успешного испытания
Рассмотрим схему Бернулли с вероятностью успеха  в одном
испытании.
Введем величину
в одном
испытании.
Введем величину  со значениями
со значениями 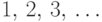 ,
равную номеру первого успешного
испытания.
,
равную номеру первого успешного
испытания.
Теорема 14.
Вероятность того, что первый успех произойдет в испытании
с номером 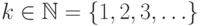 , равна
, равна 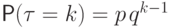 .
.
Доказательство. Вероятность первым  испытаниям завершиться неудачей,
а последнему - успехом, равна
испытаниям завершиться неудачей,
а последнему - успехом, равна

Определение 18.
Набор чисел 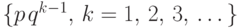 называется
геометрическим распределением вероятностей.
называется
геометрическим распределением вероятностей.
Геометрическое распределение вероятностей обладает интересным свойством, которое можно назвать свойством "нестарения".
Теорема 15.
Пусть 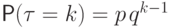 для любого
для любого  .
Тогда для любых неотрицательных целых
.
Тогда для любых неотрицательных целых  и
и  имеет
место равенство:
имеет
место равенство:

Если, например, считать величину  временем безотказной
работы
(измеряемым целым числом часов) некоторого устройства, то данному
равенству можно придать следующее звучание: вероятность работающему
устройству проработать еще сколько-то часов не зависит от того
момента, когда мы начали отсчет времени, или от того, сколько уже работает
устройство. Общепринятое название этого свойства - свойство
отсутствия последействия.
временем безотказной
работы
(измеряемым целым числом часов) некоторого устройства, то данному
равенству можно придать следующее звучание: вероятность работающему
устройству проработать еще сколько-то часов не зависит от того
момента, когда мы начали отсчет времени, или от того, сколько уже работает
устройство. Общепринятое название этого свойства - свойство
отсутствия последействия.
Доказательство. По определению условной вероятности,
 |
( 5.1) |
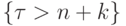 влечет событие
влечет событие 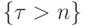 , поэтому пересечение этих
событий есть
, поэтому пересечение этих
событий есть 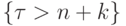 . Найдем для целого
. Найдем для целого  вероятность
вероятность  :
: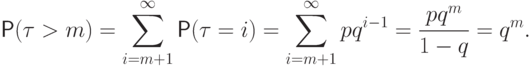
 еще проще:
событие
еще проще:
событие 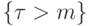 означает в точности,
что в схеме Бернулли первые
означает в точности,
что в схеме Бернулли первые  испытаний завершились неудачами,
т.е. его вероятность равна
испытаний завершились неудачами,
т.е. его вероятность равна 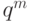 .
Возвращаясь к (5.1), получим
.
Возвращаясь к (5.1), получим