НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 3: Линейные преобразования линейных пространств столбцов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3991 / 731 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Произведение линейных отображений

Теорема 7.1.1. Если _U, _V, _W - линейные пространства над полем K,

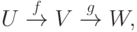
$U \stackrel{f}{\to} V \stackrel{g}{\to} W,$

f и g - линейные отображения линейных пространств, то их произведение

$h=gf: U\to W$

является линейным отображением.

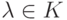Доказательство. Пусть $u,u_1,u_2\in {}_KU$ и $\lambda\in K$ . Тогда

$\begin{align*} & h(u_1+u_2) = (gf)(u_1+u_2) = g(f(u_1+u_2)) ={} \\ & \quad {}=g(f(u_1)+f(u_2)) = g(f(u_1)) + g(f(u_2))= h(u_1)+h(u_2);\\ & h(\lambda u) = (gf)(\lambda u) = g(f(\lambda u)) = g(\lambda f(u)) = \lambda (g(f(u))) = \lambda h(u). \end{align*}$

Матрица произведения линейных отображений пространств столбцов

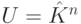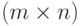Если $U=\hat K^n$ , $V=\hat K^m$ , $W=\hat K^r$ - пространства столбцов над полем K, линейное отображение $f: \hat K^n\to \hat K^m$ задается $(m\times n)$ -матрицей F=(f_ij), линейное отображение 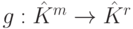$g: \hat K^m\to \hat K^r$ задается 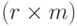$(r\times m)$ -матрицей G=(g_ij), то вычислим однозначно определенную матрицу линейного отображения $h=gf: \hat K^n\to\hat K^r$ .

Пусть

$\begin{gathe} X= \begin{pmatrix} x_1\\ \vdots\\ x_n \end{pmatrix} \in \hat K^n,\\ Y= \begin{pmatrix} y_1\\ \vdots\\ y_m \end{pmatrix} = f(X) \in \hat K^m,\quad Z= \begin{pmatrix} z_1\\ \vdots\\ z_r \end{pmatrix} = g(Y) \in \hat K^r. \end{gathe}$

Тогда для $1 \leq k \leq r$

$\begin{mult} z_k=\sum_{i=1}^{m}g_{ki}y_i = \sum_{i=1}^{m} g_{ki}\biggl(\,\sum_{l=1}^{n}f_{il}x_l\biggr)= \sum_{i=1}^{m}\sum_{l=1}^{n}g_{ki}f_{il}x_l={} \\ {}\stackrel{(*)}{=} \sum_{l=1}^{n}\sum_{i=1}^{m}g_{ki}f_{il}x_l= \sum_{l=1}^{n}\biggl(\,\sum_{i=1}^{m}g_{ki}f_{il}\biggr)x_l= \sum_{l=1}^{n}h_{kl}x_l, \end{mult}$

где

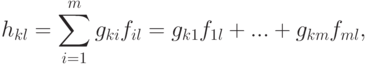
$h_{kl}=\sum_{i=1}^{m}g_{ki}f_{il}=g_{k1}f_{1l}+...+g_{km}f_{ml},$

т. е. матрицей линейного отображения h=gf является $(r\times n)$ -матрица H=(h_kl).

Замечание (*). Использованное в доказательстве равенство

$\sum_{i=1}^{m}\biggl(\,\sum_{l=1}^{n}\gamma_{il}\biggr)= \sum_{l=1}^{n}\biggl(\,\sum_{i=1}^{m}\gamma_{il}\biggr)$

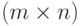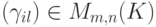означает разный порядок суммирования элементов прямоугольной $(m\times n)$ -матрицы $(\gamma_{il})\in M_{m,n}(K)$ .

Это вычисление приводит нас к следующему определению произведения согласованных по размеру матриц.

Определение 7.2.1. Пусть

$G=(g_{ij})\in M_{r,m}(K),\quad F=(f_{ij})\in M_{m,n}(K)\text{ -}$

прямоугольные матрицы согласованных размеров (т. е. длина m строки матрицы G совпадает с длиной m столбца матрицы F ). Тогда определим произведение H=GF как $(r\times n)$ -матрицу H=(h_kl), где

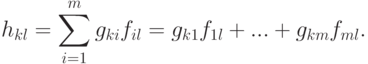
$h_{kl}=\sum_{i=1}^{m}g_{ki}f_{il}= g_{k1}f_{1l}+...+g_{km}f_{ml}.$