Оптимальное программирование процессоров EPIC-архитектуры
Оптимизация предикатных вычислений при решении задач поиска на процессоре EPIC-архитектуры
Выше указывается на существование задач, для которых основным средством решения является механизм ветвления. В процессорах "традиционной" архитектуры ветвление производится с помощью последовательных логических проверок и условных передач управления. Архитектура процессора EPIC -архитектуры предусматривает предикатный механизм, позволяющий хранить условия ветвления — булевы переменные и производить спекулятивные вычисления, т.е. выполнять операции, если указанное при них логическое переменное имеет значение ИСТИНА (1). Это значительно снижает вес условных переходов в программе (хотя и поддержанных запуском дополнительного конвейера), а то и вовсе исключает их.
Если в задачах сортировки используются анализ и пересылки отдельных элементов массива, то в задачах поиска производится совместный анализ "массив с массивом", что значительно затрудняет решение проблемы минимизации числа условных переходов.
Поиск является одним из наиболее часто встречающихся действий при программировании. Отметим важность таких задач, как текстовый анализ, выделение подструктур генетического кода, нормальные алгоритмы Маркова, кусочная аппроксимация временных рядов и др.
Задача поиска формулируется следующим образом.
Заданы массивы A = {a1, ..., an} (текст) и B = b1, ..., bm (слово, эталон). Необходимо найти первое вхождение (индекс i ) в массив A таких следующих подряд m элементов {ai, ai+1, ..., ai+m-1}, что ai+j-1 = bj, j = 1, ..., m.
Прямой поиск
Самый простой алгоритм поиска заключается в последовательном просмотре текста — элементов множества A и их сравнением с первым элементом B. При положительном результате сравниваются следующие элементы массивов и т.д. В случае появления отрицательного результата сравнения дальнейший анализ массива A продолжается со следующего элемента. Сложность этого поиска составляет O(nm).
В табл. 8.4 представлен пример прямого поиска по шагам. Каждый шаг обусловлен переходом, в случае несовпадения элементов, к анализу, начиная со следующего элемента массива A.
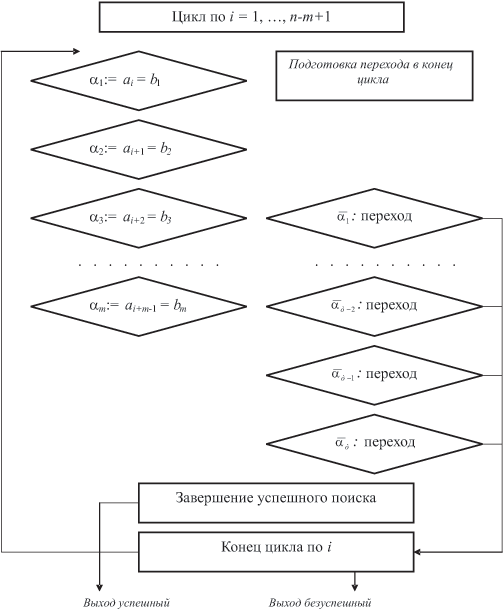
На рис. 8.6 представлен план программы прямого поиска. Каждая явно наблюдаемая строка соответствует параллельно выполняемым командам, отображенным в одном "длинном" командном слове. Столбец соответствует одному исполнительному устройству (ИУ). Внутренний цикл попарного сравнения элементов массивов показан в развернутом виде.
Предусмотрено многократное выполнение команды условного перехода на продолжение циклического перебора элементов массива A. Эти команды выполняются в спекулятивном режиме и требуют единственной подготовительной команды запуска дополнительного конвейера. В случае первого несовпадения элементов массива и эталона единственный раз выполняется условный переход.
Начальное смещение команд сравнения выполнено в предположении о необходимости двух тактов для возможного использования результата.
Следует признать высокую эффективность распараллеливания — высокий коэффициент использования ИУ и достижимость "теоретической" сложности алгоритма.