Задача логического вывода и когерентность кэш-памяти в ВС SPMD-архитектуры
Обработка базы знаний
Рассмотрим пример решения в упрощенной постановке одной из задач искусственного интеллекта — задачи полного вывода на основе системы аксиом и последующего выбора кратчайшего пути, ведущего от "посылки" из данного множества к одному из заданных "следствий". Решение этой задачи является важным элементом выбора кратчайшей последовательности управляющих воздействий, приводящих систему из одного состояния в другое. Эта же задача является важным элементом обработки базы знаний — дополнением ее новыми знаниями посредством всех возможных выводов, автоматического доказательства теорем, кибернетического моделирования (например, направленного движения по лабиринту) и т.д.
Количество логических выводов в единицу времени является основной характеристикой производительности перспективных ЭВМ. Тем выше важность исследования всех аспектов решения данной задачи и прежде всего — исследования возможности приспособления к ней архитектуры ВС.
Представим следующую модель базы знаний.
Пусть задано множество  ,
объектов-высказываний. Задана первичная система отношений следования,
которую будем называть системой аксиом, попарно связывающая объекты в пары
вида "посылка-следствие"
,
объектов-высказываний. Задана первичная система отношений следования,
которую будем называть системой аксиом, попарно связывающая объекты в пары
вида "посылка-следствие"  . Отдельно выделим множество
. Отдельно выделим множество 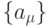 исходных
высказываний, которые в системе аксиом участвуют только как "посылки", и
множество результирующих высказываний
исходных
высказываний, которые в системе аксиом участвуют только как "посылки", и
множество результирующих высказываний 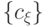 , которые в системе аксиом
участвуют только как "следствия".
, которые в системе аксиом
участвуют только как "следствия".
Остальные высказывания составляют множество 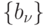 . Таким
образом,
. Таким
образом,
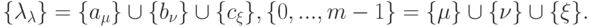
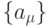 — множество входов,
— множество входов, 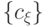 — множество выходов.)
— множество выходов.)Необходимо связать объекты-высказывания всеми возможными логическими
цепочками вида 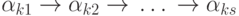 ( s — длина цепочки) на основе данной системы
аксиом, не содержащими циклы (исключающими вхождение одних и тех же объектов более
одного раза), при этом
( s — длина цепочки) на основе данной системы
аксиом, не содержащими циклы (исключающими вхождение одних и тех же объектов более
одного раза), при этом  .
.
Будем считать, что все логические цепочки, связывающие объекты-высказывания
множества 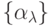 является системой
аксиом, в каждой из которых высказывание-посылка принадлежит множеству
является системой
аксиом, в каждой из которых высказывание-посылка принадлежит множеству 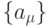 .
При этом каждая такая аксиома представляет логическую цепочку, длина которой
равна двум. Все возможные логические цепочки на основе этой системы аксиом
дополняют базу знаний до ее окончательного уже неизменяемого состояния.
.
При этом каждая такая аксиома представляет логическую цепочку, длина которой
равна двум. Все возможные логические цепочки на основе этой системы аксиом
дополняют базу знаний до ее окончательного уже неизменяемого состояния.
Примем следующий план параллельной обработки базы знаний: пусть i -й процессор выбирает очередную логическую цепочку (первый раз i -ю, затем
номер увеличивается на N ) и пытается дополнить базу знаний всеми возможными новыми
цепочками на основе продолжения данной одним объектом, не встречавшимся в ней ранее. То
есть, множество логических цепочек образует опорный массив. Если последний элемент
выбранной цепочки принадлежит множеству 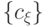 , ее продолжение
уже невозможно. Процессоры выбирают и обрабатывают логические цепочки до исчерпания возможности
изменения базы данных; чтобы обнаружить это, организуется индикация
формирования хотя бы одним процессором новой логической цепочки.
, ее продолжение
уже невозможно. Процессоры выбирают и обрабатывают логические цепочки до исчерпания возможности
изменения базы данных; чтобы обнаружить это, организуется индикация
формирования хотя бы одним процессором новой логической цепочки.
Конкретизируем пример. Пусть
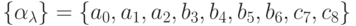 .
.
Система аксиом:
a0 -> b3, a1 -> b4, a2 -> b5, b3 -> c7, b4 -> b5, b4 -> b6, b5 -> b4, b6 -> c7, b6 -> c8.
Первые три отношения образуют три логические цепочки - начальное значение базы знаний.
Пусть d — начальный адрес в ОПД базы знаний, по которому располагается первая логическая цепочка. Каждая цепочка описывается дескриптором с пятью дескрипторными элементами, необходимыми для обработки только одним процессором. Дескрипторы в ОПД располагаются с адреса f. Таким образом, первоначально в ОПД имеем
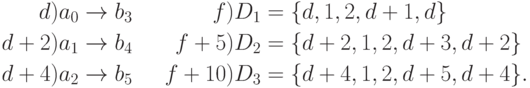
Дескриптор D0, описывающий массив дескрипторов логических цепочек, содержит восемь дескрипторных элементов и расположен в ОПД по адресу g. Его начальный вид
g) D0 = {f, 5, 3, f+10, f, f, 5N, f}.
Будем считать, что при загрузке в память процессора адреса дескрипторов совпадают с их именами.
Аксиомы, не составляющие начальное значение базы знаний, образуют в ОПД массив с начальным адресом b, описываемый дескриптором Db в памяти каждого процессора, в нашем примере Db = {b, 2, 7, b+12, b}.
И, наконец, в ОПД организован массив признаков 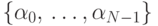 обработки
логических цепочек процессорами, описываемый дескриптором
обработки
логических цепочек процессорами, описываемый дескриптором 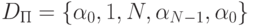 в памяти каждого процессора.
в памяти каждого процессора.
В табл. 13.1 представлена программа решения задачи, состоящая из двух частей: по командам 0-20 база знаний дополняется всеми возможными логическими цепочками, по командам 21-30 выбирается цепочка минимальной длины, соединяющая некоторое исходное высказывание с результирующим. (При движении по лабиринту так может быть найден кратчайший путь, соединяющий вход и выход, а также указаны эти вход и выход, если они в лабиринте не единственные.)
По команде 0 производится синхронизация ВС для одновременного начала выполнения следующих команд.
По команде 1 (ЗАГрузка Дескриптора) по адресу дескриптора D0 в памяти каждого процессора засылаются восемь дескрипторных элементов, хранящихся в ОПД, начиная с адреса g. Выполняются операции (D07) := (D05) := (D00)+i(D01). Эта начальная загрузка производится при первом выполнении основной части программы, после чего по команде 2 управление передается команде 4.
По команде 3, с которой начинается цикл анализа очередной логической цепочки, формируются дескрипторные элементы D02 и D03 в соответствии с тем их текущим значением, которое было выработано в ходе совместного формирования всеми процессорами логических цепочек.
По команде 4 (ВЗЯТЬ Дескриптор) выбирается дескриптор в составе всех восьми дескрипторных элементов, определенный значением дескрипторного элемента D07, и заносится по адресу Ds в памяти процессора. При первом выполнении команды (j = 0) i -м процессором выбирается дескриптор Di+1. При j -м выполнении команды этим же процессором выбирается дескриптор Di+1+Nj. При выполнении команды сначала проверяется условие принадлежности выбираемого дескриптора массиву таких дескрипторов, (D07) не больше (D03)? При выполнении этого условия дескриптор Ds на данном процессоре формируется. Выполняется операция (D07) := (D07)+(D06), что при следующем выполнении данной команды позволит выбрать дескриптор логической цепочки, номер которой на N превосходит номер выбранной. При невыполнении условия принадлежности управление передается команде 18 без модификации дескрипторного элемента D07.
Для другого применения данной команды можно предположить возможность указания по первому адресу адреса дескрипторного элемента D04, что обеспечивало бы последовательную выборку дескрипторов из массива при повторном выполнении команды в цикле без учета номера процессора.
По команде 5, выполняемой в случае, если i -й процессор приступает к обработке очередной логической цепочки, i -му элементу массива признаков присваивается значение 0.
По команде 6 выделяется признак высказывания, хранящегося по последнему адресу анализируемой цепочки (он указан в Ds3 ). Если это результирующее высказывание, сопровождаемое признаком "c", осуществляется переход на выборку дескриптора следующей логической цепочки — на выполнение команды 4. В противном случае выполняется следующая команда.
По команде 7 запоминаются значения дескрипторных элементов Ds2 и Ds3, а также восстанавливается значение дескрипторного элемента Db4.

 0
0


 >
>