НОУ ИНТУИТ | Архитектура параллельных вычислительных систем. Лекция 11: Программирование задач для асинхронной ВС архитектуры "data flow"

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет путей сообщения

Опубликован: 22.12.2006 | Доступ: свободный | Студентов: 2492 / 607 | Оценка: 4.07 / 4.02 | Длительность: 16:07:00

ISBN: 978-5-9556-0071-0

Темы: Программирование, Аппаратное обеспечение, Суперкомпьютерные технологии

Специальности: Разработчик аппаратуры

|

Вам нравится? Нравится 29 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Приводятся примеры программирования в архитектуре асинхронной ВС на принципах data flow. Рассматриваются задачи численного интегрирования, умножения матриц, решения системы линейных уравнений. Исследуются основы трансляции с языков высокого уровня.

Ключевые слова: методом "трапеций", значение, адрес, тег, программа коммутации, ПО, команда, загрузка, операции, цикла, умножение, адресный генератор, матрицы, алгоритм, коммутация, запись, обратный, коэффициенты, выражение, равенство, старший коэффициент, поиск, выход, останов, деление, вычисление, цикл команды, регистр команд, LAU, val, ID, Sisal, оптимизация программы, нормальная форма Бэкуса-Наура, польская инверсная, бесскобочная запись, решающее поле, ярусно-параллельная форма, процессор памяти, команды пересылки, цикл типа арифметической прогрессии, команда цикла, очередь заявок

Численное интегрирование

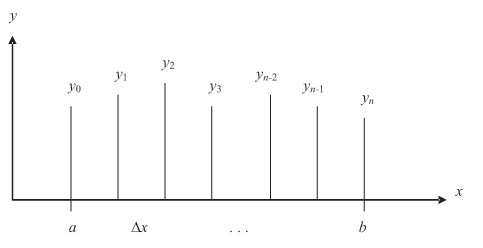
Найдем методом "трапеций" приближенное значение интеграла функции y(x) (рис. 11.1).

Рис. 11.1. Схема численного интегрирования

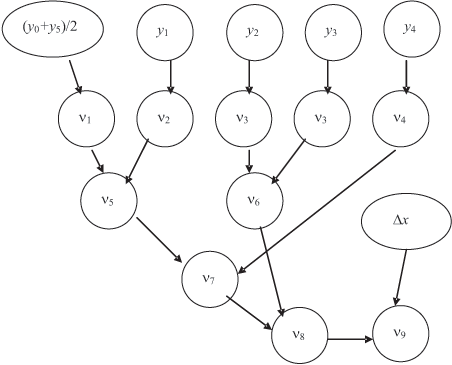
При построении программы вновь воспользуемся оптимальной схемой счета — способом "пирамиды" (рис. 11.2), приведенной на рис. 10.7 для случая n = 5. Здесь 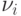$\nu _{i}$ — математические адреса вычислителей, причем 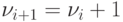$\nu _{i+1} = \nu _{i} + 1$ . (Предполагаем, что либо на адрес вычислителя указывает тег, либо он принадлежит определенной области адресного пространства.)

Рис. 11.2. Схема счёта интеграла

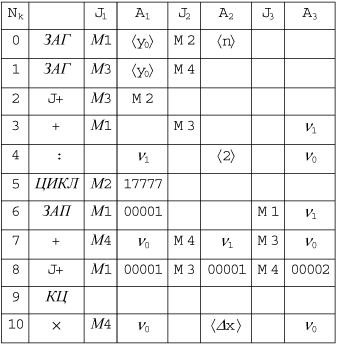
Программа коммутации приведена на рис. 11.3.

Рис. 11.3. Программа численного интегрирования

По командам 0—2 коммутируется выполнение инструкций формирования содержимого индексных регистров-модификаторов М1—М4.

По командам 3 и 4 на вычислителе с математическим адресом 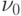$\nu _{0}$ формируется значение 0,5 x (y₀ + y_n).

Далее следует основной цикл реализации "пирамиды" — цикл на n - 1 повторений (команда 5).

По команде 6 коммутируется последовательная загрузка вычислителей $y_{1} \Rightarrow \nu _{1}; y_{2} \Rightarrow \nu _{2}; y_{n-1} \Rightarrow \nu _{n-1}$ .

По команде 7 коммутируются операции 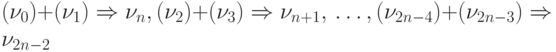$(\nu _{0})+(\nu _{1}) \Rightarrow \nu _{n} , (\nu _{2})+(\nu _{3}) \Rightarrow \nu _{n+1}, \dots , (\nu _{2n-4})+(\nu _{2n-3}) \Rightarrow \nu _{2n-2}$ .

Команда 8 служит для изменения значений индексных регистров.

Команда 9 конец цикла.

По команде 10 коммутируется умножение суммы значений функции, сформированной на вычислителе с математическим адресом $\nu _{2n-2}$ , на величину $\delta x$ .

Напомним, что порядок использования математических адресов вычислителей обусловлен только требованиями организации циклической обработки массива данных с индексацией и переадресацией, т.е. продиктован законами программирования с учетом распараллеливания. При выполнении программы регистры буферов вычислителей назначаются адресным генератором исходя из требований динамического планирования использования ресурсов.

Умножение матриц

Воспользовавшись формулой вычисления элементов матрицы C = A x B,

$C_{ij} = \sum_{k=1}^n a_{ik}b_{kj},\text{ где }i, j = 1, ..., n,$

(взяв для упрощения случай, когда все три матрицы — квадратные), запишем алгоритм умножения матриц в виде программы на некотором языке высокого уровня:

for i := 1 step 1 until n do
  for j := 1 step 1 until n do
    begin
      c[i; j] := a[i; 1] x b[1; j];
      for k := 1 step 1 until n do c[i; j] := c[i; j] + a[i; j] x b[k; j]
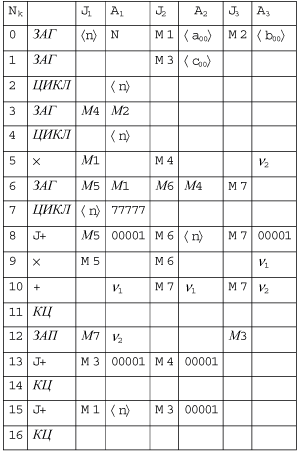
    end

Программа коммутации приведена на рис. 11.4.

Рис. 11.4. Программа умножения матриц

Дадим некоторые пояснения к ходу выполнения программы.

В команде 0 значения <a₀₀> и <b₀₀> являются адресами начала размещения элементов матриц A и B в ОПД, N — имя переменной, содержащей значение их размерности n. По команде 1 происходит загрузка адреса начала размещения элементов матрицы C.

Команда 2 начинает цикл на n повторений (этот цикл заканчивается командой 16). Команда 3 осуществляет настройку на первый столбец матрицы B.

Команда 4 начинает первый вложенный цикл на n повторений. Цикл завершается командой 14. Команда 5 коммутирует счет первого слагаемого суммы (в первый раз должно быть произведено умножение a₀₀x b₀₀ ). По команде 6 производится настройка индексных регистров, в частности, в первый раз будут выполнены действия

(M₅):= a₀₀ ; (M₆):= b₀₀ ; (M₇):=0.

Команда 7 начинает второй вложенный цикл (заканчивается командой 11). По команде 8 производится коммутация переадресации по строке матрицы A, по столбцу матрицы B и переадресации вычислителя. Команда 9 — умножение, в первый раз выполняется коммутация действия

a₀₁ x b₁₀ => 1.

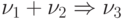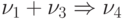По команде 10 в первый раз (т.е. при ее первом выполнении) закоммутируется выполнение действия $\nu _{1} + \nu _{2} \Rightarrow \nu _{3}$ , во второй раз — $\nu _{1} + \nu _{3} \Rightarrow \nu _{4}$ и т.д.

Команда 12 задает запись элемента матрицы C.

Команда 13 это переадресация по столбцу, а команда 15 переадресация по строке.

Дальше >>

Авторизоваться

Архитектура параллельных вычислительных систем

Программирование задач для асинхронной ВС архитектуры "data flow"

Численное интегрирование

Умножение матриц

Вопросы и ответы