Оптимальное программирование процессоров EPIC-архитектуры
Сортировка с помощью дерева
Алгоритм сортировки предполагает следующие действия.
-
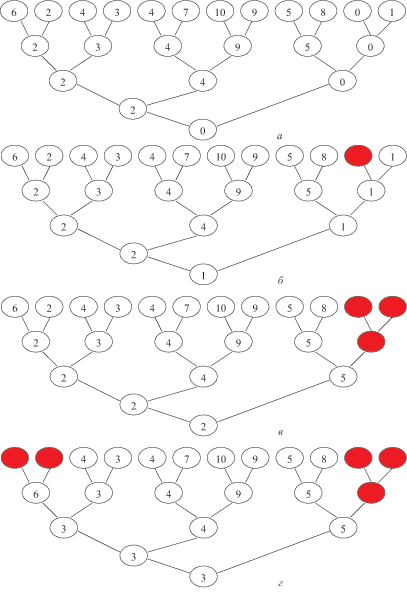
Реализуется и запоминается "пирамида" нахождения минимального элемента массива — формируется двоичное дерево, вершины которого отмечены сравниваемыми элементами массива (рис. 8.4).
- Найденный элемент исключается из рассмотрения, освобождая занятые им вершины дерева (отмечены темным).
- Элемент первого уровня сравнения переводится на освободившееся место.
- В результате попарного сравнения элементов, начиная со второго уровня, вновь отыскивается минимальный элемент и т.д.
На рис. 8.4,а представлено двоичное дерево для нахождения минимального элемента 0 в ранее рассмотренном массиве. После исключения этого элемента находится минимальный элемент 1 из оставшихся, как показано на рис. 8.4,б.
После исключения этого элемента, элемент 5, как результат первого уровня сравнений, продвигается в вершину следующего уровня. Минимальный элемент находится, как показано на рис. 8.4,в.
Следующий шаг демонстрируется на рис 8.4,г и т.д. — до полного опустошения дерева.
Данный алгоритм имеет "теоретическую" сложность O(n log2n), рассчитанную на
основе оценок числа сравнений и пересылок и не учитывающую обслуживание
древовидной структуры. Известно, что графовые структуры, которые для параллельного
компьютера на уровне обработки целесообразно представлять матрицами следования, приводят к
оценкам сложности не менее 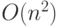 . Очевидно, что программа
анализа графического представления отношений между элементами массива сложна и трудоемка, хотя во
многом зависит от изощренности программиста. Учитывая информационную связность
процесса, многократно использующего "пирамиду" (требуется
использование средств синхронизации) при не регулярном расположении элементов (затруднено нахождение
сравниваемых элементов при динамически меняющейся структуре дерева), следует
высказать сомнение о целесообразности реализации метода на процессоре EPIC -архитектуры.
. Очевидно, что программа
анализа графического представления отношений между элементами массива сложна и трудоемка, хотя во
многом зависит от изощренности программиста. Учитывая информационную связность
процесса, многократно использующего "пирамиду" (требуется
использование средств синхронизации) при не регулярном расположении элементов (затруднено нахождение
сравниваемых элементов при динамически меняющейся структуре дерева), следует
высказать сомнение о целесообразности реализации метода на процессоре EPIC -архитектуры.
Быстрая сортировка
- Приблизительно в середине массива выбираем элемент x.
- Последовательно перебирая элементы слева, находим элемент ai > x. Если такого нет, за искомый элемент принимаем x.
- Аналогичный поиск элемента aj < x производим справа от x. Если такого нет, за искомый элемент принимаем x.
- Меняем местами элементы ai и aj в случае их неравенства.
- Продолжаем процесс, пока исходный массив не разделится на два, где левый подмассив содержит элементы, не большие всех элементов, составляющих правый подмассив.
- Шаги 1-5 применим рекурсивно для каждого из подмножеств.
Сложность данного алгоритма, учитывающая лишь операции сравнения и пересылки, но не организацию вычислений, составляет O(n log2 n).
Аппарат предикатных вычислений предусматривает симулятивный режим выполнения операций. Это означает, что минимизировать число операций (пересылок) нет необходимости, поскольку для выполнения этих операций выделены время и ресурсы, независимо от того, будут ли они выполнены. Избежать лишних пересылок можно с помощью условных переходов, но они-то и нежелательны. Кроме того, организация обмена местами элементов, когда эти места определяются в результате поиска, усложняет логику программы и адресацию данных, вносит элемент последовательного анализа.
Представим модификацию алгоритма быстрой сортировки, обеспечивающую простоту программной реализации.
- Приблизительно в середине массива выбираем элемент x.
- Сравниваем с этим элементом все элементы массива. Элементы, меньшие x, образуют множество A, элементы, равные x, образуют множество B, остальные элементы входят в множество C.
- Повторяем рекурсивно по отношению к множествам A и C (элементы B уже находятся на своем месте) шаги 1 и 2 до исчерпания образующихся подмножеств, а следовательно, до завершения сортировки.
В табл. 8.3 отображен процесс быстрой сортировки рассмотренного ранее массива. На каждом шаге производится преобразование всех сформированных на предыдущем шаге подмножеств (отмечены фигурными скобками), т.е. всего массива. Курсивом выделены элементы, относительно которых производится разбиение подмножеств.
Программу целесообразно планировать на основе циклически запускаемой процедуры разбиения каждого ранее сформированного подмножества вида A и C на три новых, как указано в модифицированном алгоритме. При этом множества вида B пропускаются, так как для их элементов сортировка закончена.
| Исходный массив | 6 | 2 | 4 | 3 | 4 | 7 | 10 | 9 | 5 | 8 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шаг 1 | {6 | 2 | 4 | 3 | 4 | 5 | 0 | 1} | {7} | {10 | 9 | 8} |
| Шаг 2 | {2 | 0 | 1} | {3} | {4 | 4} | {6 | 5} | 7 | {8} | {9} | {10} |
| Шаг 3 | {0} | {2 | 1} | 3 | 4 | 4 | {5} | {6} | 7 | 8 | 9 | 10 |
| Шаг 4 | 0 | {1} | {2} | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Однако опытный программист здесь может обнаружить "скрытые" пересылки, обусловленные необходимостью "склеивания" динамически формируемых подмассивов, с их неопределенным, переменным началом. Необходимо учесть, что каждое разбиение на подмножества не меняет их суммарную длину. То есть подмножества формируются "на том же месте", и пересылки носят локальный характер внутри одних подмножеств, не нарушая структуру и расположение других.
При организации программы разбиения массива приходится все же пользоваться значительным объемом дополнительной памяти. Только подмассив A может располагаться (накапливаться) с начала разбиваемого массива. Подмассивы B и C, во избежание многократной коррекции расположения, целесообразно накапливать отдельно. При этом начала подмассивов A и B, а также B и C, должны отстоять друг от друга не менее чем на длину разбиваемого массива.
Экономия памяти достигается лишь тем, что после каждого разбиения производится "склейка" массивов A, B и C на месте разбитого массива.
Следует учесть, что каждое расширение используемой памяти приводит к увеличению числа "промахов" при обращении в кэш, а потому нежелательно.
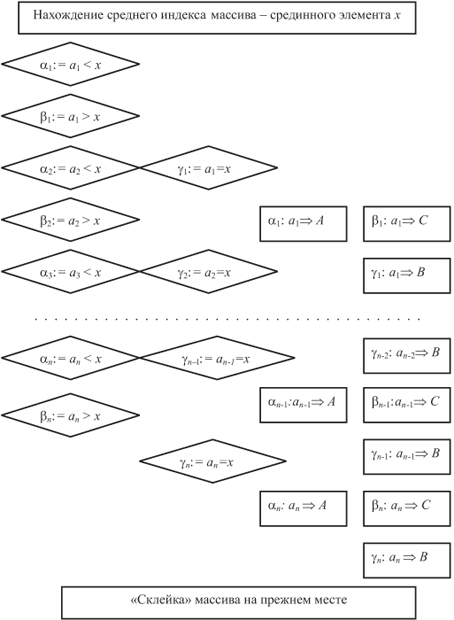
План выполнения основной процедуры разбиения в применении к исходному массиву,в виде "развернутого" цикла, показан на рис. 8.5.
Таким образом, разбиение может производиться с использованием дополнительной памяти и продолжаться до вырождения подмножеств, что в конечном итоге приведет к получению упорядоченного массива.
Необходимо отметить, что время выполнения программы существенно зависит от организации кэша. Ведь сложность, помимо временной составляющей, имеет составляющую, отражающую затраты памяти. Так, если большой массив представляется в кэше по частям, то совместная обработка элементов, близко расположенных в памяти, имеет более низкую вероятность "промаха", чем элементов, далеко отстоящих друг от друга. Это замечание может служить еще одним доводом в пользу модифицированной пузырьковой сортировки.
Быстрая сортировка требует значительного увеличения затрат сверхоперативной памяти, что на деле может снизить быстродействие, т.к. приводит к увеличению числа "промахов" при обращении в кэш и, следовательно, к росту степени использования операционной системы в вычислительном процессе.
В этом отношении модифицированная "пузырьковая" сортировка универсальна, проста в реализации и не требует дополнительных ресурсов памяти.
Сортировка методом прямого включения также дает хорошую загрузку исполнительных устройств. Однако необходимость синхронизации пересылок на последнем этапе выполнения основной процедуры нахождения минимального элемента массива методом "пирамиды" может приводить к "разреженности" в выполнении команд во времени, к появлению пропущенных тактов. Следует учесть и необходимое увеличение вдвое объема используемой памяти.
Другие известные методы сортировки, как правило, ресурсоемки и не реализуют "теоретическую" сложность алгоритмов при программной реализации, включая программы процессора EPIC -архитектуры.
Таким образом, отметим, что EPIC -архитектура наиболее приспособлена к реализации
двух модифицированных методов сортировки: "пузырьковой" и быстрой.
Сложность первой — 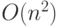 , сложность второй, улучшенной,
— O(n log2 n). Программная
реализация этих методов достаточно проста, затраты на управление выполнением
программы (индексация, циклы) минимальны. Принцип предикатных вычислений и
спекулятивного режима выполнения операций дает значительный эффект и исключает
применение условных переходов. Он позволяет полностью загружать работой
исполнительные устройства процессора, обеспечивая высокую эффективность
распараллеливания.
, сложность второй, улучшенной,
— O(n log2 n). Программная
реализация этих методов достаточно проста, затраты на управление выполнением
программы (индексация, циклы) минимальны. Принцип предикатных вычислений и
спекулятивного режима выполнения операций дает значительный эффект и исключает
применение условных переходов. Он позволяет полностью загружать работой
исполнительные устройства процессора, обеспечивая высокую эффективность
распараллеливания.