Оптимальное программирование процессоров EPIC-архитектуры
Пузырьковая сортировка
Алгоритм этой сортировки заключается в последовательном сравнении и смене
мест (если необходимо) пар соседних элементов массива. Процесс продолжается до тех
пор, пока обмены не прекратятся. Сложность алгоритма также составляет 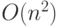 .
.
Легко видеть, что последовательный учет результатов предыдущего сравнения (последовательное всплытие "пузырьков") не допускает распараллеливания. Алгоритм нуждается в модификации.
Для эффективного распараллеливания на процессоре EPIC -архитектуры необходимо при одном обзоре массива отделить процедуру сравнения элементов и формирования значений предикатов от процедуры пересылки, т.е. организовать множественное всплытие "пузырьков".
Для этого при каждом обзоре текущее (частично упорядоченное) множество элементов разбивается на пары. При первом (нечетном) обзоре первая пара включает первый элемент массива. При втором (четном) обзоре группирование начинается со второго элемента и т.д. Внутри пар элементы упорядочиваются, при необходимости меняясь местами так, чтобы слева стоял меньший элемент. Наличие обменов при каждом просмотре фиксируется. Их прекращение свидетельствует об окончании сортировки массива.
Ниже по шагам (обзорам) отражена сортировка ранее рассмотренного массива. Формируемые на каждом шаге пары элементов выделены. При четном n нечетные шаги сортировки требуют анализа k = n/2 пар элементов, четные шаги требуют анализа k = (n/2) - 1. При нечетном n k = [n/2] пар элементов.
План программы (внутренний цикл развернут) представлен на рис. 8.3.
Здесь 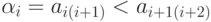 ; индексация выполнена с
учетом попеременного формирования пар соседних элементов и с учетом их переименования после
пересылки; k — индекс последней анализируемой пары элементов;
; индексация выполнена с
учетом попеременного формирования пар соседних элементов и с учетом их переименования после
пересылки; k — индекс последней анализируемой пары элементов;  — предикат, принимающий значение "1",
если операция, при которой он указан, выполняется. Предполагается, что при
выходе за границу массива операция над элементами не производится. Далее
предполагается возможность взаимного обмена данными, инициированная в одном командном слове.
— предикат, принимающий значение "1",
если операция, при которой он указан, выполняется. Предполагается, что при
выходе за границу массива операция над элементами не производится. Далее
предполагается возможность взаимного обмена данными, инициированная в одном командном слове.
Программа не предполагает использование условных переходов и соответствует "теоретической" сложности, хотя время выполнения алгоритма при данной комплектации АЛУ сокращается почти в четыре раза по сравнению с применением одного ИУ.
Сортировка Шелла
Данный метод относится к "улучшенным". Он предполагает последовательные этапы разбиения исходного массива на несколько групп и их независимую сортировку.
Однако следует с осторожностью относиться к "улучшенным" методам сортировки, требующим значительных подготовительных работ и ориентированным на человека — вычислителя, для которого логический анализ действий не представляется сложным, а потому выносится за область учета трудоемкости. В компьютерной программе должно быть все учтено посредством формализованных действий.
На ранее выбранном массиве продемонстрируем сортировку Шелла.
Сначала выполняется четверная сортировка: группируются и сортируются элементы массива, отстоящие друг от друга на расстоянии 4. Рассматриваемый массив будет разбит на четыре группы элементов: A1 = {6, 4, 5}, A2 = {2, 7, 8}, A3 = {4, 10, 0}, A4 = {3, 9, 1}. Каждая группа сортируется одним из известных способов. Элементы возвращаются в массив с соблюдением тех же начала и расстояния, с которыми они извлекались. Тогда результатом четверной сортировки будет последовательность 4, 2, 0, 1, 5, 7, 4, 3, 6, 8, 10, 9.
На втором проходе элементы полученной последовательности перегруппировываются — теперь каждый элемент группы отстоит от другого на две позиции. В данном случае сформируются две группы: B1 = {4, 0, 5, 4, 6, 10} и B2 = {2, 1, 7, 3, 8, 9}. Сортировка внутри групп ( двойная сортировка) и возвращение в исходный массив на соответствующие места приводят к последовательности 0, 1, 4, 2, 4, 3, 5, 7, 6, 8, 10, 9.
На третьем проходе окончательно производится обычная ( одинарная ) сортировка всей последовательности, при которой число пересылок сведено до минимума.
Исследования по выбору расстояний привели к теоретическому обоснованию оценки сложности алгоритма, как O(n1,2). Эта сложность основана на минимизации требуемых пересылок.
Вполне очевидно, как существенно усложняется логика программы. Кроме того, если в заключение все равно необходимо выполнить единичную сортировку, то при планировании спекулятивного режима в рамках предикатных вычислений совершенно безразлично, выполняется ли операция пересылки, на которую выделены время и средства, или нет. Так что действительная сложность алгоритма, достигаемая на компьютере, значительно превосходит сложность алгоритмов сортировки, рассмотренных ранее.
Применение данного метода, очевидно, нецелесообразно на процессоре EPIC -архитектуры.