НОУ ИНТУИТ | Моделирование систем. Лекция 11: Оценивание параметров линейной модели по наблюдениям неполного ранга

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3283 / 1985 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 30 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Практическая часть

2.1. Оценка параметров модели наблюдений неполного ранга с помощью обобщенной обратной матрицы

Пример 1. Для заданной матрицы регрессоров неполного ранга и вектора значений функции отклика произведите оценку линейной регрессионной модели. Рассчитайте остаточную сумму квадратов RSS. Постройте зависимость RSS от одного из компонент вектора коэффициентов (параметров) линейной регрессионной модели.

Исходные данные

Матрица регрессоров:

$X= \left[\begin{array}{ccccc} 3.4022&3.0252&3.5178&3.8696&1.3751\\ -1.8649&10.2522&4.2463&4.6709&4.6601\\ 0.3741&10.3820&-1.9841&-2.1825&4.7191\\ 4.3259&-3.8260&4.3070&4.7377&-1.7391\\ 3.3377&10.4823&2.0589&2.2648&4.7647\\ 4.6759&10.2461&-2.2197&-2.4417&4.6573\\ 2.2459&1.9426&-0.7720&-0.8492&0.8830 \end{array}\right],$

вектор значений функции отклика (вектор наблюдений):

$Y= \left[\begin{array}{c} 13.784\\ 13.617\\ 12.968\\ 14.713\\ 13.864\\ 12.847\\ 14.420 \end{array}\right].$

Сначала следует определить линейно зависимые столбцы и произвести преобразование матрицы с целью расположения первых линейно независимых столбцов. Величина будет равняться рангу матрицы. Как известно, столбцы матрицы — линейно зависимые, если значения одного столбца отличаются от значений другого столбца на постоянный множитель. Порядок расположения в матрице регрессоров не отразится на результате произведения этой матрицы на искомые коэффициенты линейной модели, если в таком же порядке произвести перестановку искомых коэффициентов.

Программный код решения примера:

clear,clc,close
% Исходные данные
% Матрица регрессоров
X = [1.340, 1.630, -4.240, 2.412, 5.088;
     1.610, 1.900, -3.970, 2.898, 4.764;
     1.470, 1.760, -4.110, 2.646, 4.932;
     2.610, 2.900, -2.970, 4.698, 3.564;
     3.000, 3.290, -2.580, 5.400, 3.096;
     2.040, 2.330, -3.540, 3.672, 4.248;
     1.060, 1.470, -4.520, 1.908, 5.424];
% Вектор наблюдений - вектор выхода
Y = [13.784;13.617;12.968;14.713;13.864;12.847;14.420];
% Размерность вектора наблюдений
n = length(Y);
% Размерность искомого вектора коэффициентов линейной модели
p = size(X,2);
%%-------------------------------------------
% Вычисление ранга матрицы регрессоров
rankX = rank(X);

if rankX == p %% модель полного ранга
fprintf('\n Размерность вектора параметров модели: p = %d\n Модель наблюдений полного ранга: rank(X) = %d\n', p, rankX);
B = inv(X'*X)*X'*Y;
disp(' ')
disp(' Оценка вектора параметров B: ')
disp(B)

YY = X*B;
fprintf('\n Y - заданный вектор наблюдений;\n');
fprintf(' YY - расчетный вектор наблюдений;\n');
fprintf(' Error - относительная погрешность;\n');
fprintf('\tY\t\t\tYY\t\t Error\n');
 
erd = abs(Y-YY)./abs(Y)*100;
for J = 1 : length(Y)
    fprintf(' %1.4f\t %1.4f\t %1.4f%%\n', Y(J), YY(J), erd(J));
end
 
 RESS = (Y-YY)'*(Y-YY);
 Cp = mean(abs(Y-YY)./abs(Y)*100);
 fprintf('\n Величина RSS: %g\n', RESS);
 fprintf(' Усредненная погрешность расчета вектора наблюдения: %g%%\n', Cp);
return
end
%% модель наблюдений неполного ранга
fprintf('\n Размерность вектора параметров модели: p = %d\n',p);
fprintf(' Модель наблюдений неполного ранга: rank(X) = %d\n', rankX);
% Определение номеров линейно зависимых столбцов
k1 = 0;
for N = 1 : p
    for J = 1 : p
        op = abs(X (:,J))./abs(X (:,N));
        Pr(1:n,1) = op;
str = sprintf('%1.5f', Pr(1));
str2 = sprintf('%1.5f', Pr(end));

if str2num(str) == str2num(str2) & str2num(str) ~= 1 
    k1 = k1 + 1;
     NJ(k1,1:2) = [N,J];
        end
     end
end
 
k2 = 0;
en = size(NJ,1);
for I = 1 : size(NJ,1)
    for J = 1 : size(NJ,2)
       if NJ(I,J) == NJ(en-J+1,2)
           k2 = k2 + 1;
EX(k2) = (en-J+1);
       end
    end
end
NJ(EX,:) = []
for J = 1 : size(NJ,1)
fprintf(' Столбец %d линейно зависит от столбца %d\n', NJ(J,2), NJ(J,1));
end
%%-------------------------------------------
X0 = X(:,1:rank(X));
X1 = X(:, rank(X)+1:end);
S = X'*X; %% информационная матрица

% Формирование g-обратной матрицы
B11 = inv(X0'*X0);
B12 = zeros(rank(X), p-rank(X));
B21 = zeros(p-rank(X), rank(X));
B22 = zeros(p-rank(X),p -rank(X) );
Sg = [B11, B12;B21,B22] % g-обратная матрица
H = Sg*S;
z = randn(size(X,2), 1); %%случайный вещественный вектор
P11 = inv(X0'*X0)*X0'*Y;
P21 = zeros(p - rank(X), 1);
% Z11 = zeros(rank(X));
% Z12 = inv(X0'*X0)*X0'*X1;
% Z21 = zeros(p - rank(X), rank(X));
% Z22 = -eye((p - rank(X)));
%  B = [P11;P21]+ [Z11,Z12;Z21,Z22]*z

Ep = eye(p);
B = [P11;P21] + [H - Ep]*z;
disp(' ')
disp(' Оценка вектора параметров B: ')
disp(B)
YY = X*B;
fprintf('\n Y - заданный вектор наблюдений;\n');
fprintf(' YY - расчетный вектор наблюдений;\n');
fprintf(' Error - относительная погрешность;\n');
fprintf('\tY\t\t\tYY\t\t Error\n');
 
erd = abs(Y-YY)./abs(Y)*100;
for J = 1 : length(Y)
    fprintf(' %1.4f\t %1.4f\t %1.4f%%\n', Y(J), YY(J), erd(J));
end
 
 RESS = (Y-YY)'*(Y-YY);
 Cp = mean(abs(Y-YY)./abs(Y)*100);
 fprintf('\n Величина RSS: %g\n', RESS);
 fprintf(' Усредненная погрешность расчета вектора наблюдения: %g%%\n', Cp);
Bopt = B;
 k = 2;
 d = 0;
 for J = 0.79*Bopt(k) : 0.01 : 1.21*Bopt(k)
     d = d + 1;
     B(k) = J;
     YY = X*B;
      RESS(d) = (Y-YY)'*(Y-YY);
      Xres(d) = J;
 end
 kmin = find(RESS == min(RESS));
 bmin = Xres(kmin);

fig1 =  figure(1);
set(fig1,'name','Зависимость RSS от параметра')
 line(Xres, RESS, 'linew', 2)
 grid on

ch = sprintf('%sОптимальное значение %d-го параметра: %s(%d) = %g','\bf\fontsize{11}\fontname{times}', 
  k, strcat('\beta', '_{opt}'), k,bmin);
 title(ch);
 
ylabel('\bf\fontsize{12}\fontname{times}RSS');
ch2=sprintf('%s_%d','\bf\fontsize{12}\fontname{times}\beta',k);
 xlabel(ch2);

В программе предусмотрен вариант расчета вектора параметров линейной регрессионной модели для случая наблюдений полного ранга. Если имеется полный ранг, то расчет ведется по решению нормального уравнения, в котором информационная матрица — не вырожденная. Притом с помощью оператора 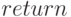return прекращается дальнейшее выполнение программы.

В программе усредненная погрешность расчета вектора параметра – это средняя величина от столбца относительной погрешности в процентах.

В программе произведено изменение 2-го параметра регрессионной модели. Его изменение выполнено слева и справа от оптимального значения.

Результат выполнения программы

Размерность вектора параметров модели: p = 5
 Модель наблюдений неполного ранга: rank(X) = 3
 Столбец 4 линейно зависит от столбца 1
 Столбец 5 линейно зависит от столбца 3

Sg =
  116.6611 -112.7327   -7.3650         0         0
 -112.7327  109.0775    7.1933         0         0
   -7.3650    7.1933    0.5164         0         0
         0         0         0         0         0
         0         0         0         0         0
 
 Оценка вектора параметров B: 
   -7.8809
   10.5189
   -0.9992
   -0.2349
    0.5978

 Y - заданный вектор наблюдений;
 YY - расчетный вектор наблюдений;
 Error - относительная погрешность;
	Y	  YY		 Error
 13.7840	 13.2973	 3.5308%
 13.6170	 13.4319	 1.3592%
 12.9680	 13.3621	 3.0392%
 14.7130	 13.9305	 5.3187%
 13.8640	 14.1249	 1.8817%
 12.8470	 13.6463	 6.2216%
 14.4200	 14.4200	 0.0000%

 Величина RSS: 1.74575
 Усредненная погрешность расчета вектора наблюдения: 3.05018%

Диаграмма зависимости RSS от величины 2-го компонента вектора параметров показана на рис. 11.1.

Рис. 11.1. Зависимость RSS от 2-го компонента вектора параметров модели

Задание 1

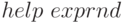Вектор определите с помощью функции (см. $help\mbox{ }exprnd$ ). В качестве параметра функции примите номер компьютера, на котором выполняется лабораторная работа (1, 2, 3, ...).
Вектор определите с помощью равномерного закона распределения вероятностей из интервала , где — номер компьютера, на котором выполняется лабораторная работа (1, 2, 3, ...).
При расчете вектора наблюдений ( 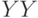) произведите его "зашумление" случайным вектором, распределенным по стандартному нормальному закону.
Постройте зависимость RSS от числа прогонов программы. Число принять от 1 до , где — номер компьютера, на котором выполняется лабораторная работа (1, 2, 3, ...).
Напишите программу по определению линейно независимых столбцов и расположению их на первые мест матрицы регрессоров.
Найдите оценку параметров модели неполного ранга (по данным примера 1) с помощью псевдообратной матрицы Мура-Пенроуза (см. $help\mbox{ }pinv$ ).

Пример 2. Вычислите коэффициенты 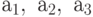$а_{1},\mbox{ }а_{2},\mbox{ }а_{3}$ уравнения линейной регрессии $y = a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3}$ при следующем заданном множестве измерений эксперимента:

Таблица 11.1.
Результаты измерений эксперимента
$x_{1}$	0.620	0.400	0.420	0.820	0.660	0.720	0.380	0.520	0.450	0.690	0.550	0.360
$x_{2}$	12.000	14.200	14.600	12.100	10.800	8.200	13.000	10.500	8.800	17.000	14.400	12.800
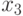$x_{3}$	5.890	3.800	3.990	7.790	6.270	6.840	3.610	4.940	4.275	6.555	5.225	3.420
	51.60	49.90	48.50	50.60	49.70	48.80	42.60	45.90	37.80	64.80	53.40	45.30

Данные, приведенные в таблице 11.1, взяты с некоторыми изменениями из [7].

Составим матрицу регрессоров :

$X= \left[\begin{array}{ccc} 0.620&12.000&5.890\\ 0.400&14.200&3.800\\ 0.420&14.600&3.990\\ 0.820&12.100&7.790\\ 0.660&10.800&6.270\\ 0.720&8.200&6.840\\ 0.380&13.000&3.610\\ 0.520&10.500&4.940\\ 0.450&8.800&4.275\\ 0.690&17.000&6.555\\ 0.550&14.400&5.225\\ 0.360&12.800&3.420 \end{array}\right].$

Составим вектор наблюдений :

$Y= \left[\begin{array}{c} 51.60\\ 49.90\\ 48.50\\ 50.60\\ 49.70\\ 48.80\\ 42.60\\ 45.90\\ 37.80\\ 64.80\\ 53.40\\ 45.30 \end{array}\right].$

Программный код решения примера:

clear,clc
%% Исходные данные
%% Матрица регрессоров
X = [0.620, 12.000, 5.890;
    0.400,  14.200, 3.800;
    0.420,  14.600, 3.990;
    0.820,  12.100, 7.790;
    0.660,  10.800, 6.270;
    0.720,   8.200, 6.840;
    0.380,  13.000, 3.610;
    0.520,  10.500, 4.940;
    0.450,   8.800, 4.275;
    0.690,  17.000, 6.555;
    0.550,  14.400, 5.225;
    0.360,  12.800, 3.420];
%% Вектор наблюдений - вектор выхода
Y = [51.60;49.90;48.50;50.60;49.70;48.80;42.60;45.90;37.80;...
64.80;53.40;45.30];
% Размерность вектора параметров - коэффициентов модели
p = size(X,2);
% Размерность вектора наблюдений
n = length(Y);
rankX = rank(X);
 if rankX == p %% модель полного ранга
fprintf('\n Размерность вектора параметров модели: 
  p = %d\n Модель наблюдений полного ранга: rank(X) = %d\n', p, rankX);
B = inv(X'*X)*X'*Y;
disp(' ')
disp(' Оценка вектора параметров B: ')
disp(B)
return
end
%% модель наблюдений неполного ранга
fprintf('\n Размерность вектора параметров модели: p = %d\n',p);
fprintf(' Модель наблюдений неполного ранга: rank(X) = %d\n', rankX);
% Определение номеров линейно зависимых столбцов
k1 = 0;
for N = 1 : p
    for J = 1 : p
        op = abs(X (:,J))./abs(X (:,N));
        Pr(1:n,1) = op;
str = sprintf('%1.4f', Pr(1));
str2 = sprintf('%1.4f', Pr(end));
 
if str2num(str) == str2num(str2) & str2num(str) ~= 1 
    k1 = k1 + 1;
     NJ(k1,1:2) = [N,J];
        end
     
   end
end
 
k2 = 0;
en = size(NJ,1);
for I = 1 : size(NJ,1)
    for J = 1 : size(NJ,2)
       
       if NJ(I,J) == NJ(en-J+1,2)
           k2 = k2 + 1;
     EX(k2) = (en-J+1);
       end

    end
end
 
for J = 1 : size(NJ(EX),1)
fprintf(' Столбец %d линейно зависит от столбца %d\n', NJ(J,2), NJ(J,1));
end
 
X0 = X(:,1:rank(X));
X1 = X(:, rank(X)+1:end);
S = X'*X; %% информационная матрица
 
% Формирование g-обратной матрицы
A11 = inv(X0'*X0);
A12 = zeros(rank(X), p-rank(X));
A21 = zeros(p-rank(X), rank(X));
A22 = zeros(p-rank(X),p -rank(X) );
Sg = [A11, A12;A21,A22]; % g-обратная матрица

% Определение решения нормального уравнения
H = Sg*S;
z = randn(size(X,2), 1); %%случайный вещественный вектор

P11 = inv(X0’*X0)*X0’*Y;
P21 = zeros(p - rank(X), 1);

% Z11 = zeros(rank(X));
% Z12 = inv(X0’*X0)*X0’*X1;
% Z21 = zeros(p - rank(X), rank(X));
% Z22 = -eye((p - rank(X)));
%  A = [P11;P21]+ [Z11,Z12;Z21,Z22]*z
 
Ep = eye(p);
A = [P11;P21] + [H - Ep]*z;

disp(‘ ‘)
disp(' Оценка вектора параметров A: ')
disp(A)

Результат выполнения программы

Размерность вектора параметров модели: p = 3
Модель наблюдений неполного ранга: rank(X) = 2
Столбец 3 линейно зависит от столбца 1
 
 Оценка вектора параметров A: 
   54.4373
    2.4329
   -2.1269

Задание 2

Проведите сравнение заданного вектора наблюдений и расчетного вектора наблюдений. Рассчитайте относительную погрешность по каждому значению векторов и определите усредненную относительную погрешность.
Рассчитайте остаточную сумму квадратов RSS.
Произведите "зашумление" расчетного вектора наблюдений случайным вектором, распределенным по нормальному закону с параметрами 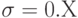$\mu = –0.Х$ , $\sigma = 0.Х$ , где — номер компьютера, за которым выполняется лабораторная работа (1, 2, 3, ...). Выполните два предыдущих пункта задания.
Выполните решение примера с помощью псевдообратной матрицы Мура–Пенроуза. Сравните результаты для случая применения -обратной матрицы.

Контрольные вопросы

Каковы условия вырожденности информационной матрицы в нормальном уравнении?
Что такое остаточная сумма квадратов?
Каким свойствам должна удовлетворять псевдообратная матрица Мура–Пенроуза?
Каким основным свойством обладает обобщенная обратная матрица?
В каком случае модель будет моделью неполного ранга?
Что такое регрессоры?

Дальше >>

Авторизоваться

Моделирование систем

Оценивание параметров линейной модели по наблюдениям неполного ранга

Практическая часть

2.1. Оценка параметров модели наблюдений неполного ранга с помощью обобщенной обратной матрицы

Исходные данные

Контрольные вопросы

Вопросы и ответы