НОУ ИНТУИТ | Моделирование систем. Лекция 8: Введение в дисперсионный анализ

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Мордовский государственный университет имени Н.П. Огарева

Опубликован: 30.11.2010 | Доступ: свободный | Студентов: 3291 / 1988 | Оценка: 4.12 / 4.13 | Длительность: 14:37:00

ISBN: 978-5-9963-0352-6

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист, Системный архитектор

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Практическая часть

1. Однофакторный дисперсионный анализ с одинаковым числом испытаний на различных уровнях

Рассмотрим пример однофакторного анализа, данные которого позаимствованы из [12].

Пример 1. В результате семикратного измерения параметров алюминиевой фольги для электротехнических конденсаторов с использованием двух способов измерения получены значения удельной емкости заформованной фольги (таблица 8.4), считая, что удельная емкость фольги распределена по гауссовскому (нормальному) закону, а образцы принадлежат одному рулону, заформованному на одном агрегате при постоянных технологических режимах. Требуется оценить систематические ошибки измерения.

Таблица 8.4.
Данные примера
Способ измерения (уровни фактора)	Дублирующие опыты
	1	2	3	4	5	6	7
	Удельная емкость образцов фольги, мкФ/дм2
1-й способ	9.12	9.30	8.20	10.50	9.80	8.50	10.20
2-й способ	8.34	8.58	8.18	8.42	8.66	8.26	8.50

Так как ставится задача изучения влияния одного качественного фактора — способа измерения, применим однофакторный дисперсионный анализ при числе параллельных (дублирующих) опытов m = 7 при числе уровней факторов N = 2 .

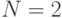Программный код решения примера:

clear, clc

% ПОВТОРНЫЕ НАБЛЮДЕНИЯ ДЛЯ ДВУХ УРОВНЕЙ ФАКТОРА
A1 = [9.12 9.30 8.20 10.50 9.80 8.50 10.20];
A2 = [8.34 8.58 8.18 8.42 8.66 8.26 8.50];
Ygk = [A1;A2];
N = 2; % ЧИСЛО УРОВНЕЙ ФАКТОРА
m = length(A1); % ЧИСЛО ПОВТОРНЫХ НАБЛЮДЕНИЙ
% СРЕДНЕЕ КАЖДОЙ СЕРИИ НАБЛЮДЕНИЙ
Yg = mean([A1',A2']); 

% СРЕДНЕЕ ВСЕХ НАБЛЮДЕНИЙ
Ycp = mean(mean([A1,A2])) %% Ycp = (sum(Yg)/N)
%-----------------------------------------------------------
fprintf('\n\t ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ:\n')
fprintf('\t Число уровней фактора: N = %d\n', N)
fprintf('\t Число дублирующих наблюдений: m = %d\n', m)
fprintf('\t Средние значения дублирующих наблюдений: \n\t Yg(%d) = %g\n\t Yg(%d) = %g\n'...
    ,1,Yg(1),2,Yg(2))
fprintf('\t Среднее значение всех наблюдений:\n\t Ycp = %g\n', Ycp)
%-----------------------------------------------------------
% ФОРМИРОВАНИЕ СУММЫ КВАДРАТОВ ОТКЛОНЕНИЙ
% ВНУТРИ СЕРИЙ НАБЛЮДЕНИЙ
So = 0;
for k = 1 : N
    for r = 1 : m
        So = So + sum(sum(Ygk(k,r) - Yg(k))^2);
    end
end
%-----------------------------------------------------------
% ФОРМИРОВАНИЕ СУММЫ КВАДРАТОВ ОТКЛОНЕНИЙ
% МЕЖДУ СЕРИЯМИ НАБЛЮДЕНИЙ
Sx = 0;
for g = 1 : N
    Sx = Sx + m*sum((Yg(g) - Ycp)^2);
end
%-----------------------------------------------------------
S = So + Sx;
fprintf(' Общая сумма квадратов отклонений отдельных наблюдений от общего среднего:\n\t S = %g\n',S)
D = S/(N*m-1);
fprintf('\t Несмещенная общая оценка дисперсии по всем N*m (%d*%d = %d) наблюдениям:\n\t D = %g\n',N,m,N*m,D)
So2 = So/(N*(m - 1));
Sx2 = Sx/(N - 1);
fprintf(' Выборочная дисперсия So2 внутри серий с числом степеней свободы Kmax = %d\n\t So2 = %g\n',N*(m - 1),So2)
fprintf(' Выборочная дисперсия Sx2 внутри серий с числом степеней свободы Kmin = %d\n\t Sx2 = %g\n',N - 1,Sx2)
fprintf('\n\t РЕЗУЛЬТАТЫ АНАЛИЗА:\n')
Fpac = Sx2/So2;
Kx = N - 1;
Ko = N*(m - 1);
fprintf('\t Число степеней свободы в эксперименте:\n\t Kx = %d\n\t Ko = %d\n',Kx,Ko)
%-----------------------------------------------------------
% КРИТИЧЕСКОЕ ЗНАЧЕНИЕ КРИТЕРИЯ ФИШЕРА Fish
% ПРИ ВЕРОЯТНОСТИ 0.95 
h = 0.01;
r1 = 0 : h : 1000;
F = fcdf(r1,Kx,Ko);
for k = 1:length(r1)
if F(k) >= 0.95 & F(k) < 0.9501
     F95 = F(k);
     Fish = r1(k);
   break    
end
end
%-----------------------------------------------------------
fprintf('\t Расчетное значение критерия Фишера: Fpac = %g\n',Fpac)
fprintf('\t Критическое значение распределения Фишера при уровне значимости a = 0.05: F = %g\n\n',Fish)
if Fpac > Fish
disp(' 1) ВЛИЯНИЕ ФАКТОРА ЗНАЧИМО')
disp(' 2) СПОСОБЫ ИЗМЕРЕНИЙ ИМЕЮТ РАЗЛИЧНЫЕ СИСТЕМАТИЧЕСКИЕ ОШИБКИ')
else
disp(' 3) ВЛИЯНИЕ ФАКТОРА - СПОСОБА ИЗМЕРЕНИЯ НЕ ЗНАЧИМО')
disp(' 4) СПОСОБЫ ИЗМЕРЕНИЙ ИМЕЮТ СИСТЕМАТИЧЕСКИЕ ОШИБКИ ОДНОГО ПОРЯДКА')
end

Результаты выполнения программы для уровня значимости критерия Фишера, равного 0.05

ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
	 Число уровней фактора: N = 2
	 Число дублирующих наблюдений: m = 7
	 Средние значения дублирующих наблюдений: 
	 Yg(1) = 9.37429
	 Yg(2) = 8.42
	 Среднее значение всех наблюдений:
	 Ycp = 8.89714
Общая сумма квадратов отклонений отдельных наблюдений от общего среднего:
	 S = 7.71029
Несмещенная общая оценка дисперсии по всем N*m (2*7 = 14) наблюдениям:
	 D = 0.593099
Выборочная дисперсия So2 внутри серий с числом степеней свободы:
          Kmax = 12
	 So2 = 0.376914
Выборочная дисперсия Sx2 внутри серий с числом степеней свободы:
 Kmin = 1
	 Sx2 = 3.18731

	 РЕЗУЛЬТАТЫ АНАЛИЗА
	 Число степеней свободы в эксперименте:
	 Kx = 1
	 Ko = 12
	 Расчетное значение критерия Фишера: Fpac = 8.45634
Критическое значение распределения Фишера при уровне значимости
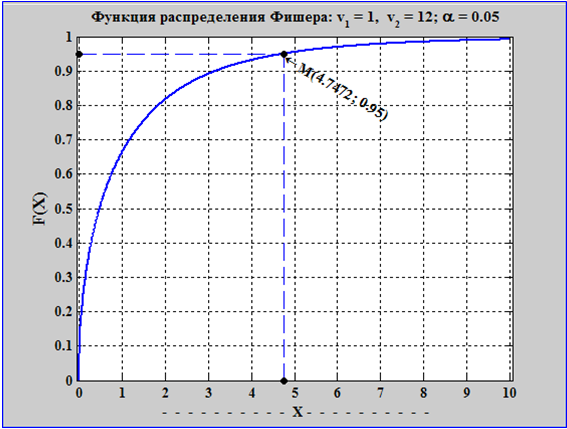
 a = 0.05: F = 4.75

 1) ВЛИЯНИЕ ФАКТОРА ЗНАЧИМО
 2) СПОСОБЫ ИЗМЕРЕНИЙ ИМЕЮТ РАЗЛИЧНЫЕ СИСТЕМАТИЧЕСКИЕ ОШИБКИ

Примечание. Критическое значение распределения Фишера можно определить по таблицам, которые составлены для различных уровней значимости и приводятся во многих учебниках по теории вероятности и математической статистике [1, 2], где указывается также число степеней свободы — в данном случае эти числа соответствуют числителю и знаменателю расчетного значения критерия Фишера.

Пояснение к определению критического значения распределения Фишера показано на рис. 8.1, где представлена интегральная функция распределения Фишера с заданными степенями свободы.

Рис. 8.1. Интегральная функция распределения Фишера

Задание 1

Напишите программу построения диаграммы, приведенной на рис. 8.1.
Произведите дисперсионный анализ в случае, когда число уровней фактора будет равно 3. Дополнительный уровень сформируйте по данным наблюдений 1-го уровня: с помощью функции в интервалах между значениями наблюдений. Например, если 1-е наблюдение равно 9.12, 2-е равно 9.3, то первое значение для дополнительного уровня взять по равномерному закону из интервала и т. д.
Напишите программу формирования массива критических точек распределения Фишера на основе функции (см. ) или на основе функции 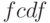(см. вышеприведенную программу) при следующих параметрах (числом степеней свободы 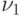, 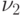и уровне значимости ):
- 1-й компьютер: $\nu_1 = 1 : 10,\qquad\nu_2 = 1 : 7,\qquad\alpha = 0.05;$
- 2-й компьютер: $\nu_1 = 1 : 7,\qquad \nu_2 = 1 : 9,\qquad\alpha = 0.025;$
- 3-й компьютер: $\nu_1 = 1 : 9,\qquad \nu_2 = 1 : 10,\qquad\alpha = 0.1;$
- 4-й компьютер: $\nu_1 = 1 : 12,\qquad\nu_2 = 1 : 8,\qquad\alpha = 0.15;$
- 5-й компьютер: $\nu_1 = 1 : 15,\qquad\nu_2 = 1 : 9,\qquad\alpha = 0.1;$
- 6-й компьютер: $\nu_1 = 1 : 9,\qquad \nu_2 = 1:10,\qquad\alpha = 0.06;$
- 7-й компьютер: $\nu_1 = 1 : 12,\qquad\nu_2 = 1 : 8,\qquad\alpha = 0.07;$
- 8-й компьютер: $\nu_1 = 1 : 15,\qquad\nu_2 = 1 : 9,\qquad\alpha = 0.08;$
- 9-й компьютер: $\nu_1 = 1 : 7,\qquad \nu_2 = 1 : 8,\qquad\alpha = 0.05;$
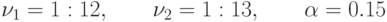- 10-й компьютер: $\nu_1 = 1 : 12,\qquad\nu_2 = 1 : 13,\qquad\alpha = 0.15$ .