|
Так это же динамическое программирование на основе математической индукции. |
Регулярные позиномы
Определение и основные свойства регулярных позиномов
В общем случае решение задачи ГП (даже без дополнительных ограничений) требует выполнения довольно сложных вычислительных процедур. Поэтому понятным является желание выделить позиномы специального вида, для которых решение задачи ГП находится просто. Именно такими являются регулярные позиномы, о которых речь пойдет ниже.
Позином
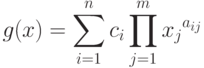 |
( 23) |
называется регулярным позиномом, если выполнены равенства:
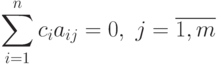 |
( 24) |
или в векторной форме записи
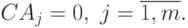
Равенства (24) означают, что для регулярного позинома
точка 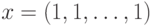 является стационарной, то
есть точкой, в которой все частные производные позинома
является стационарной, то
есть точкой, в которой все частные производные позинома  равны нулю.
равны нулю.
Пример 21 Рассмотрим следующий позином одной переменной: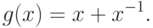
Вектор коэффициентов и матрица экспонент позинома  имеют
вид:
имеют
вид:
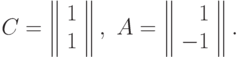
Поскольку выполнено равенство 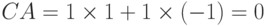 , то позином является
регулярным. Мы получим это же равенство, если вычислим значение производной
, то позином является
регулярным. Мы получим это же равенство, если вычислим значение производной  при
при 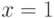 :
:
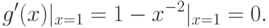
Пример 22 Проверим, что позином
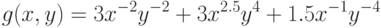
(
25)
Вектор коэффициентов и матрица экспонент позинома  имеют вид:
имеют вид:
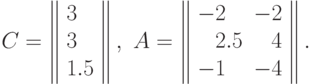
Поскольку выполнены равенства
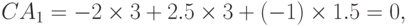

позином (25) регулярный.
Из определения следует, что позином 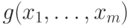 регулярен
тогда и только тогда, когда все его компоненты
регулярен
тогда и только тогда, когда все его компоненты 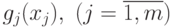 регулярны. Например, у позинома
(25) из примера 22 - регулярны обе его
компоненты:
регулярны. Например, у позинома
(25) из примера 22 - регулярны обе его
компоненты:
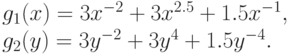 |
( 26) |
Приведем теорему, которая в ряде случаев упрощает проверку регулярности позинома.
Теорема 4 Если 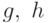 - регулярные позиномы, то
- регулярные позиномы, то 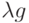 (
( 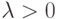 ),
), 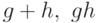 ,
,  (
(  , целое число) -
тоже регулярные позиномы.
, целое число) -
тоже регулярные позиномы.
Пример 23 Докажем, используя теорему 4, что функция
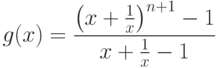
(
27)
Прежде всего, заметим, что формула (27) является
формулой суммы 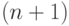 члена геометрической прогрессии, у которой
члена геометрической прогрессии, у которой 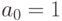 , а
, а  :
:
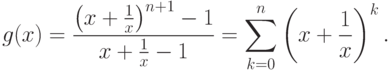 |
( 28) |
В примере 21 было доказано, что позином  регулярный. Следовательно, по
теореме 4 функции
регулярный. Следовательно, по
теореме 4 функции 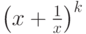 при целом
при целом  также являются регулярными позиномами. Тогда (по той же теореме)
функция
также являются регулярными позиномами. Тогда (по той же теореме)
функция  является регулярным позиномом как сумма регулярных
позиномов.
является регулярным позиномом как сумма регулярных
позиномов.
Минимизация регулярных позиномов
Наименьшие значения регулярных позиномов легко вычисляются, так как имеет место факт, который мы сформулируем как теорему (см., например, [1]).
Теорема 5 Наименьшее значение регулярного позинома 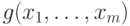 равно сумме его коэффициентов и достигается при
равно сумме его коэффициентов и достигается при 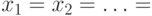
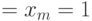 :
:
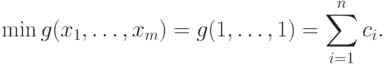
Из теоремы 5 не следует, что регулярный позином
достигает своего минимума только в точке 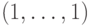 .
Например, для регулярного позинома
.
Например, для регулярного позинома
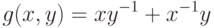
точкой минимума являются все точки вида  при
при  .
.
Значение позинома 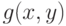 во всех этих точках равно 2. Однако
легко доказать, что регулярный позином одной переменной имеет
единственный минимум в точке
во всех этих точках равно 2. Однако
легко доказать, что регулярный позином одной переменной имеет
единственный минимум в точке  .
.
Пример 24 Вычислим минимальные значения регулярных позиномов из примеров 22 и 23 соответственно:
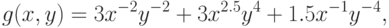
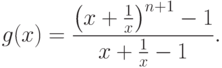
В соответствующих примерах было доказано, что обе функции являются регулярными позиномами, поэтому по теореме 5 имеем:
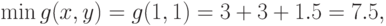
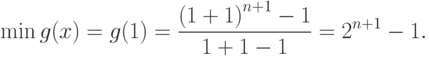
Главная теорема о позиномах
Из теории дифференциального исчисления известно, что необходимыми
условиями того, что точка 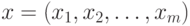 -
экстремум функции
-
экстремум функции  , является равенство нулю частных
производных
, является равенство нулю частных
производных  в этой точке:
в этой точке:
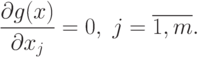 |
( 29) |
Точки, которые удовлетворяют условиям (29), называются стационарными.
Не все стационарные точки являются точками экстремума. Установить, является ли стационарная точка экстремумом и каким (максимумом или минимумом), можно с помощью специальных критериев (достаточных условий экстремума). Однако в случае позиномов все гораздо проще: необходимые условия (29) являются и достаточными условиями. Остановимся на этом поподробнее.
Когда функция  является позиномом:
является позиномом:
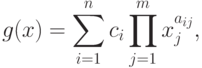
условия (29) принимают вид:
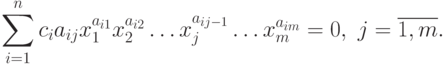 |
( 30) |
Умножив каждое уравнение системы (30) на
соответствующее ему  , получим эквивалентную систему
уравнений:
, получим эквивалентную систему
уравнений:
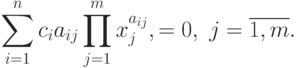 |
( 31) |
Теперь мы сформулируем теорему, на которую будем ссылаться как на главную теорему о позиномах. %, а также следствие из нее. То, что мы поместили эту теорему именно в этом месте, объясняется тем, что самое короткое ее доказательство основано на преобразовании произвольного позинома в регулярный позином. Разумеется, речь идет о позиноме, достигающего своего минимума в области определения.
Теорема 6 Все положительные решения системы
(31) являются точками глобального минимума позинома  .
.
