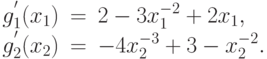|
Так это же динамическое программирование на основе математической индукции. |
Регулярные позиномы
Оценки минимума позинома
Учитывая главную теорему о позиномах, мы далее будем говорить о минимумах, опуская прилагательное глобальный.
Задачи, которые рассматриваются в этом курсе, заключаются в нахождении значения минимума позинома и одной или всех точек, в которых он достигается, разумеется, если таковые имеются. Однако в ряде случаев бывает достаточно (или полезно) знать не точное значения минимума, а его оценки. Приведем сначала необходимые определения.
Нижней оценкой функции  называется любое вещественное
число
называется любое вещественное
число 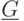 , для которого при любом
, для которого при любом  из области
определения функции
из области
определения функции  выполнено неравенство
выполнено неравенство  . Очевидно, что любая нижняя оценка функции является
нижней оценкой минимума этой функции и наоборот.
. Очевидно, что любая нижняя оценка функции является
нижней оценкой минимума этой функции и наоборот.
Не так обстоит дело с верхними оценками. Верхней оценкой
минимума функции  называется любое вещественное число
называется любое вещественное число  , для которого выполнено неравенство
, для которого выполнено неравенство 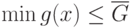 . Очевидно, что любая верхняя оценка функции
является верхней оценкой ее минимума, но не любая верхняя
оценка минимума является верхней оценкой функции.
. Очевидно, что любая верхняя оценка функции
является верхней оценкой ее минимума, но не любая верхняя
оценка минимума является верхней оценкой функции.
Знание оценок минимума позинома бывает полезно по двум основным
причинам. Во-первых, во многих алгоритмах вычисления организованы
таким образом, что знание оценок часто сокращает время работы
алгоритма. Во-вторых, в ряде случаев, когда разность  мала, можно не вычислять точное
значение минимума, положив
мала, можно не вычислять точное
значение минимума, положив  .
.
Обсудим сначала получение нижних оценок. Обозначим через  - позином, являющийся суммой только тех из мономов (образующих
позином
- позином, являющийся суммой только тех из мономов (образующих
позином  ), номера которых включены в множество
), номера которых включены в множество  :
:

Обозначим через

Так как 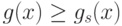 при любом
при любом  , то любая из величин
, то любая из величин  является нижней оценкой для минимума
является нижней оценкой для минимума  :
:
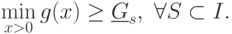
При 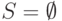 полагаем
полагаем  и получаем
тривиальную нижнюю оценку
и получаем
тривиальную нижнюю оценку 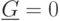 . На практике в
качестве
. На практике в
качестве  следует выбирать подмножества, для которых величина
следует выбирать подмножества, для которых величина  легко вычисляется, например, когда позином
легко вычисляется, например, когда позином  является регулярным.
является регулярным.
Перейдем теперь к обсуждению верхних оценок. Верхней оценкой
минимума позинома является его значение при любом  . Так
как проще всего вычислить значение позинома в точке
. Так
как проще всего вычислить значение позинома в точке 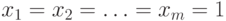 , то в качестве тривиальной верхней оценки обычно
берут
, то в качестве тривиальной верхней оценки обычно
берут
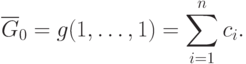
Прежде, чем описать, как можно вычислить более точные верхние
оценки позинома, напомним, что компонентами позинома  называются позиномы
называются позиномы 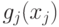 :
:
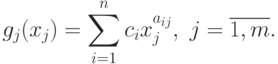
Заметим, что позиномы 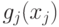 получаются в результате
выполнения следующей замены переменных:
получаются в результате
выполнения следующей замены переменных:
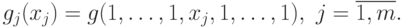
Более точную верхнюю оценку можно получить, вычислив минимумы
компонент позинома 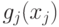 , которые являются функциями от
одной переменной. Обозначим через
, которые являются функциями от
одной переменной. Обозначим через
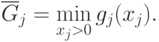
Любая из оценок  , так как
справедливо неравенство:
, так как
справедливо неравенство:
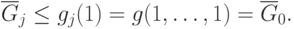
В качестве верхней оценки минимума позинома  может быть
использована следующая величина:
может быть
использована следующая величина:
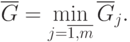
Приведем пример вычисления оценoк позинома.
Пример 25 Вычислим оценки позинома:

Вычислим сначала нижнюю оценку позинома. Для этого представим
первый моном 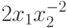 как сумму двух равных мономов:
как сумму двух равных мономов:
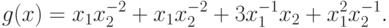
Возьмем ![S=[2, 3, 4]](/sites/default/files/tex_cache/de74cd2b508c7ecec3506527de4c4c22.png) . Позином
. Позином
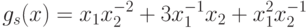
является регулярным, так как для него выполнены следующие равенства:


Следовательно, его минимум вычисляется по формуле:

Таким образом, получили нижнюю оценку для позинома 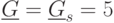 .
.
Вычислим теперь верхнюю оценку минимума позинома. Позином состоит из двух компонент:
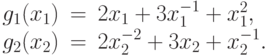
Вычислим минимумы компонент позинома. Для каждой компоненты запишем производную: