|
Так это же динамическое программирование на основе математической индукции. |
Задача ГП без ограничений
Постановка задачи
Задача геометрического программирования без ограничений
заключается в нахождении положительного вектора 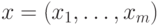 , при котором значение позинома
, при котором значение позинома  будет
наименьшим:
будет
наименьшим:
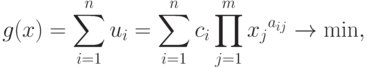

Введем специальные обозначения для индексных множеств задачи ГП:
![I=[1, 2, \ldots, n],\ J=[1, 2, \ldots, m].](/sites/default/files/tex_cache/362b8cb59c194686206c1a06f94470c4.png)
Эти обозначения удобно использовать, когда не важен порядок
перечисления индексов, поэтому в таких случаях записи  и
и  , а также
, а также  будут эквивалентны.
будут эквивалентны.
Примеры задач оптимизации с позиномами
В этой лекции в качестве примеров мы приведем постановки задач оптимизации с позиномами без ограничений.
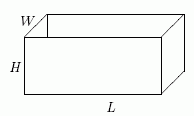
Пример 13 Требуется перевезти  кубометров угля из шахты на
завод. Для транспортировки угля необходимо
изготовить открытый прямоугольный контейнер. Стоимость материала,
идущего на изготовление боковых сторон
и дна контейнера, составляет
кубометров угля из шахты на
завод. Для транспортировки угля необходимо
изготовить открытый прямоугольный контейнер. Стоимость материала,
идущего на изготовление боковых сторон
и дна контейнера, составляет  (руб. за квадратный
метр), на фронтальные стороны
-
(руб. за квадратный
метр), на фронтальные стороны
-  (руб. за квадратный метр). Стоимость доставки одного контейнера не зависит
от его размера и составляет
(руб. за квадратный метр). Стоимость доставки одного контейнера не зависит
от его размера и составляет  (руб.).
(руб.).
Затраты на доставку угля складываются из транспортных расходов и стоимости материала, идущего на изготовление контейнера, в котором он будет перевозиться. Требуется выбрать размеры контейнера, при которых эти затраты будут минимальны.
Обозначим через  - длину,
- длину,  - ширину и
- ширину и  - высоту
контейнера. Тогда контейнер будет использоваться
- высоту
контейнера. Тогда контейнер будет использоваться 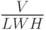 раз. Тогда транспортные расходы
равны
раз. Тогда транспортные расходы
равны  (руб.). Стоимость материала,
потраченного на изготовление фронтальных сторон, составит
(руб.). Стоимость материала,
потраченного на изготовление фронтальных сторон, составит 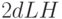 (руб.), боковых сторон -
(руб.), боковых сторон - 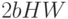 (руб.), дна
-
(руб.), дна
- 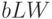 (руб.).
(руб.).
Таким образом, задача свелась к минимизации позинома, выражающего суммарные затраты:
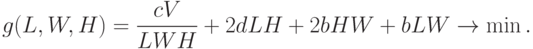 |
( 18) |
Пример 14
Корыто имеет форму полуцилиндра (рис. 2.2). При каких размерах его вес
будет минимальным, если толщина стенок равна  , емкость равна
, емкость равна  , а удельный вес материала равен -
, а удельный вес материала равен -  ?
?
Обозначим через  - внутренний радиус корыта,
- внутренний радиус корыта,  -
внутреннюю длину. Тогда вес торцовых стенок равен
-
внутреннюю длину. Тогда вес торцовых стенок равен
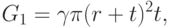
вес остальной части корыта равен
![G_{2} =\frac{1}{2} \gamma l [ \pi (r + t)^{2} - \pi r^{2}]
=\frac{\gamma \pi t}{2} l (2 r + t).](/sites/default/files/tex_cache/39ee1c5f4c65e010d6a3d0d41f498a08.png)
Так как 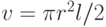 , то
, то  и
и
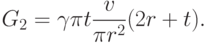
Следовательно, вес корыта равен
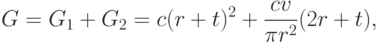
где 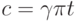 , или
, или
![G = c \left[ r^2 + 2 rt + t^2 + \frac{2 v}{\pi r} + \frac{vt}{\pi r^2} \right],](/sites/default/files/tex_cache/8e36250b7001c944a99c7b621b925e19.png)
или
![G = c \left[ r^2 + 2 rt + t^2 +\frac{2 b}{r} + \frac{bt}{r^2}\right],](/sites/default/files/tex_cache/225675547978af10dc428975eb99b97d.png)
где  .
.
Таким образом, задача свелась к минимизации позинома:
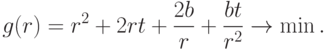 |
( 19) |
Пример 15 Работа, затрачиваемая на сжатие 1 кг воздуха в поршневом
компрессоре от давления 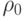 до давления
до давления  (
( 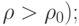 отношение
отношение 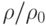 называется степенью сжатия),
выражается формулой
называется степенью сжатия),
выражается формулой
![A = RT_{0}\frac{\gamma}{\gamma - 1}\left[
\left(\frac{\rho}{\rho_0}\right)^{(\gamma - 1)/\gamma} -
1\right],](/sites/default/files/tex_cache/89f1d9d5bc951313d1f6aca76c70c29b.png) |
( 20) |
где  - так называемая газовая постоянная,
- так называемая газовая постоянная, 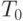 -
абсолютная температура воздуха до сжатия,
-
абсолютная температура воздуха до сжатия, 
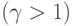 - некоторая постоянная, учитывающая конструктивные особенности
компрессора. Для получения высоких давлений делают
многоступенчатые компрессорные установки, состоящие из нескольких
последовательно соединенных компрессоров (ступеней) с холодильными
устройствами между ступенями. Пусть проектируется
- некоторая постоянная, учитывающая конструктивные особенности
компрессора. Для получения высоких давлений делают
многоступенчатые компрессорные установки, состоящие из нескольких
последовательно соединенных компрессоров (ступеней) с холодильными
устройствами между ступенями. Пусть проектируется  -ступенчатая
компрессорная установка и предполагается воздух, поступающий
в любую из ступеней, охлаждать до температуры
-ступенчатая
компрессорная установка и предполагается воздух, поступающий
в любую из ступеней, охлаждать до температуры  . Требуется
при заданных
. Требуется
при заданных 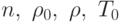 определить такие
промежуточные значения давлений
определить такие
промежуточные значения давлений 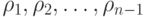 , чтобы работа, затрачиваемая на весь
процесс сжатия, была минимальна.
, чтобы работа, затрачиваемая на весь
процесс сжатия, была минимальна.
По формуле (20) работа, затрачиваемая на сжатие воздуха в  -й ступени, равна
-й ступени, равна
![A_{i} = RT_{0}\frac{\gamma}{\gamma -
1}\left[\left(\frac{\rho_i}{\rho_{i-1}}\right)^{{(\gamma-1)}/ \gamma}
- 1\right], \ i = \overline{1,n}, \ \rho_n= \rho.](/sites/default/files/tex_cache/e15322a2a47b68f7a009593147e89e43.png)
Следовательно, при выбранных 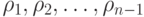 работа, затрачиваемая на весь процесс сжатия, выразится формулой
работа, затрачиваемая на весь процесс сжатия, выразится формулой
![A = \sum\limits_{i = 1}^{n}A_{i} = RT_{0}\frac{\gamma}{\gamma -
1} \left[ \sum\limits_{i=1}^{n}\left(\frac{\rho_i}{\rho_{i-1}}\right)^{{(\gamma-1)}/ \gamma}
- n\right].](/sites/default/files/tex_cache/7f5292783705f7958cbb4789c178d57b.png)
Таким образом, задача свелась к нахождению наименьшего значения позинома:
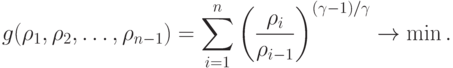 |
( 21) |
Теперь можно сказать, что задачи из примеров 13, 14, 15 - это задачи ГП.
В некоторых случаях оптимальное решение задачи ГП можно получить при помощи теоремы 2 из лекции 1. Приведем примеры.
Пример 16 Решим задачу геометрического программирования
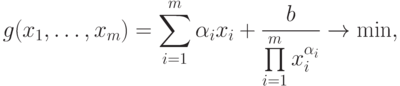
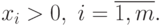
Предполагается, что 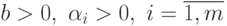 .
Обозначим через
.
Обозначим через 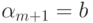 ,
, 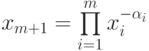 . Тогда
. Тогда 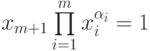 . Во введенных
обозначениях задача с позиномом
. Во введенных
обозначениях задача с позиномом 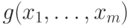 принимает вид:
принимает вид:
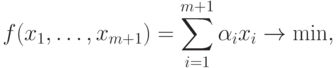
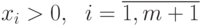
при ограничении
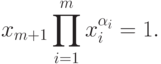
Воспользуемся теоремой 2 при 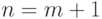 ,
,  ,
, 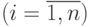 ,
, 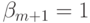 ,
,  ,
, 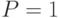 :
:

причем минимум достигается в единственной точке
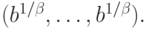
{Пример 15 (продолжение). Найдем теперь решение получившейся задачи ГП:
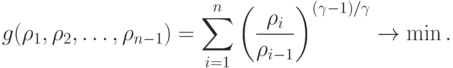
Обозначим через
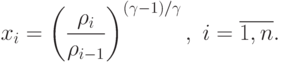
Тогда сумма  равна константе, так как выполнено следующее равенство:
равна константе, так как выполнено следующее равенство:
![\prod\limits_{i=1}^{n}x_i =
\left[\prod\limits_{i=1}^{n}\left(\frac{\rho_i}{\rho_{i-1}}\right)\right]^{(\gamma-1)/\gamma}
= \left(\frac{\rho}{\rho_0}\right)^{(\gamma-1)/\gamma}.](/sites/default/files/tex_cache/308862511be0aa36dfd10dd0509be6be.png)
Воспользуемся теоремой 2
при 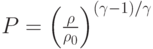 ,
, 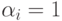 ,
, 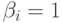 ,
, 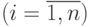 :
:
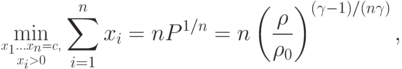
и достигается он только при 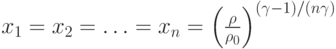 .
.
Система уравнений
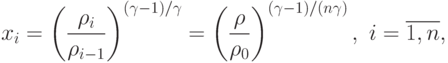
имеет положительное решение
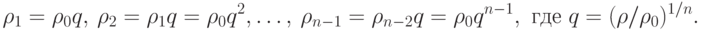
Таким образом, работа, затрачиваемая на  -ступенчатый процесс
сжатия газа, минимальна, когда на всех ступенях степени сжатия
одинаковы и равны
-ступенчатый процесс
сжатия газа, минимальна, когда на всех ступенях степени сжатия
одинаковы и равны  , то есть числа
, то есть числа 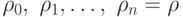 образуют геометрическую прогрессию
со знаменателем
образуют геометрическую прогрессию
со знаменателем  .
.
В следующих лекциях мы вернемся к задачам из примеров 14, 15 и решим их.