|
Так это же динамическое программирование на основе математической индукции. |
Задача ГП без ограничений
Понижение размерности задачи ГП
В общем случае сложность решения экстремальной задачи растет с ростом числа переменных, входящих в задачу. Принято это число называть размерность задачи. Для многих задач ГП размерность задачи может быть уменьшена с помощью простых преобразований.
Пусть требуется минимизировать позином

Матрицей экспонент позинома называется 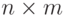 -матрица
-матрица 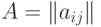 , каждый столбец которой образован показателями
степеней соответствующей переменной
, каждый столбец которой образован показателями
степеней соответствующей переменной  . Будем обозначать через
. Будем обозначать через 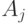 столбец
столбец  этой матрицы.
этой матрицы.
Напомним определение из курса линейной алгебры. Говорят, что
столбец 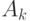 матрицы
матрицы  является линейной комбинацией остальных столбцов этой матрицы, если можно
указать такие вещественные числа
является линейной комбинацией остальных столбцов этой матрицы, если можно
указать такие вещественные числа 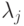 , что выполняются
равенства
, что выполняются
равенства
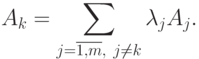 |
( 22) |
Пример 17 Покажем, что в матрице экспонент позинома

имеет место линейная зависимость столбцов.
Матрица экспонент позинома  имеет вид:
имеет вид:
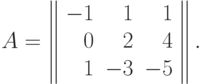
Третий столбец этой матрицы является линейной комбинацией первых
двух столбцов с коэффициентами 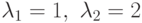 :
:
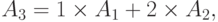

Наличие линейной зависимости столбцов в матрице экспонент упрощает решение задачи ГП. Приведем теорему, которая показывает, в чем именно заключается это упрощение.
Теорема 3 Пусть столбец 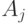 матрицы экспонент
матрицы экспонент  позинома
позинома  является линейной комбинацией
других столбцов. Обозначим через
является линейной комбинацией
других столбцов. Обозначим через  - позином от
- позином от 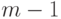 переменной,
получающийся при подстановке в позином
переменной,
получающийся при подстановке в позином  переменной
переменной 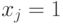 :
:

Тогда в предположении, что обе функции достигают своих минимумов, верны следующие утверждения:
-
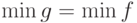 ;
; - если
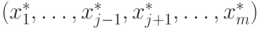 - точка минимума позинома
- точка минимума позинома  , то
, то 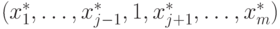 - точка минимума позинома
- точка минимума позинома  .
.
Процедуру понижения размерности задачи ГП можно повторять до тех пор, пока
все столбцы не станут линейно независимыми.
Таким образом, количество возможных шагов понижения размерности задачи ГП ограничено
максимальным числом линейно независимых столбцов матрицы экспонент  . Далее будем
обозначать это число через
. Далее будем
обозначать это число через  и называть рангом матрицы
и называть рангом матрицы  .
.
Таким образом, если ранг  меньше числа переменных задачи
меньше числа переменных задачи  ,
то задача минимизации исходного позинома от
,
то задача минимизации исходного позинома от  переменных может
быть сведена к задаче минимизации позинома от
переменных может
быть сведена к задаче минимизации позинома от  переменных.
Приведем пример.
переменных.
Приведем пример.
Пример 17(продолжение). Понизим размерность задачи

применив теорему 3}.
Ранее было показано, что третий столбец матрицы
экспонент этого позинома является линейной комбинацией остальных
столбцов: 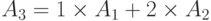 .
Поэтому по теореме 3 минимальное значение позинома
.
Поэтому по теореме 3 минимальное значение позинома  совпадает с минимальным значением позинома
совпадает с минимальным значением позинома  :
:

Матрица экспонент 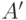 позинома
позинома  (получается удалением из матрицы
(получается удалением из матрицы  столбца
столбца 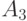 ) имеет вид:
) имеет вид:

Очевидно, что столбцы матрицы 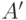 линейно независимы,
следовательно, ее ранг (как и ранг матрицы
линейно независимы,
следовательно, ее ранг (как и ранг матрицы  ) равен 2.
) равен 2.
В случае существования линейной зависимости столбцов матрицы экспонент можно поступить по-другому - понизить размерность задачи, выполнив замену переменных. Приведем примеры.
Пример 18 Понизим размерность задачи
Переменные  и
и  входят во все мономы в
виде комбинации
входят во все мономы в
виде комбинации 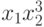 . Выполним замену
. Выполним замену 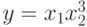 . Получим позином
. Получим позином

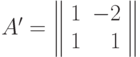
Пример 19 Понизим размерность задачи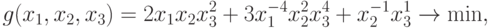
Заметим, что комбинация  входит во все мономы в
различных степенях. Выполним замену
входит во все мономы в
различных степенях. Выполним замену  , тогда
получим позином
, тогда
получим позином

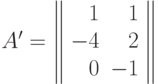
Число переменных задачи далее не может быть уменьшено.
Рассмотрим пример, в котором линейная зависимость некоторых столбцов видна сразу, но есть еще и неочевидная зависимость.
Пример 20 Понизим размерность задачи

Заметим, что комбинация  входит во все мономы в
различных степенях. Выполнив замену
входит во все мономы в
различных степенях. Выполнив замену 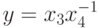 ,
получим позином
,
получим позином


Третий столбец этой матрицы является линейной комбинацией первых
двух столбцов с коэффициентами 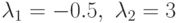 :
:
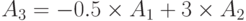 ,
,

По теореме 3 вместо минимизации позинома

можно минимизировать позином

Матрица экспонент этого позинома получается удалением из матрицы
позинома  третьего столбца:
третьего столбца:
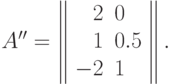
Очевидно, что столбцы матрицы  линейно независимы,
следовательно, ее ранг (как и ранг матрицы позинома
линейно независимы,
следовательно, ее ранг (как и ранг матрицы позинома  ) равен 2.
Число переменных больше не может быть уменьшено и необходимо
решить задачу минимизации позинома
) равен 2.
Число переменных больше не может быть уменьшено и необходимо
решить задачу минимизации позинома 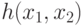 .
.
Краткие итоги
Сформулирована задача геометрического программирования без ограничений. Описана процедура понижения размерности задачи в случае очевидной и неочевидной линейной зависимости.
