|
Так это же динамическое программирование на основе математической индукции. |
Неравенство Коши и его обобщения
О термине "геометрическое программирование"
Геометрическое программирование (ГП) - раздел математического программирования, изучающий подход к решению нелинейных задач оптимизации специальной структуры. Термин геометрическое программирование впервые ввели в 1967 году Р. Даффин, Э. Питерсон и К. Зенер в монографии "Geometric Programming - Theory and Application". Русский перевод этой монографии появился в 1972 г. ([5]). Авторы объясняют появление этого названия тем, что одним из краеугольных камней излагаемой теории является неравенство между средним геометрическим и средним арифметическим и его обобщения. Добавим также, что первоначальной базой для ГП послужили некоторые геометрические задачи и методы их решения. Именно геометрия с древнейших времен занималась, в частности, решением задач на отыскание фигур, обладающих определенными экстремальными свойствами. Для решения таких задач часто использовалось геометрическое неравенство Коши и его обобщения. Одной из самых известных задач этого класса является, так называемая, задача Дидоны.
Задача Дидоны
Задача Дидоны, или классическая изопериметрическая задача, формулируется следующим образом: среди замкнутых плоских кривых, имеющих заданную длину, найти кривую, охватывающую максимальную площадь.
Эту задачу связывают с именем Дидоны - основательницы города Карфаген и его первой царицы. Согласно легенде, финикийская царевна Дидона (Элисса), спасаясь от преследований своего брата, царя Тира, отправилась на запад вдоль берегов Средиземного моря искать себе прибежище. Ей приглянулось место на побережье нынешнего Тунисского залива. Дидона вступила в переговоры с местным предводителем Ярбом о продаже земли. Запросила она совсем немного - столько, сколько можно окружить бычьей шкурой. Дидоне удалось уговорить Ярба. Сделка состоялась, и тогда хитроумная Дидона изрезала шкуру быка, которую ей предоставили местные жители, на узкие полоски, связала их и окружила территорию, на которой основала крепость, а вблизи от нее - город Карфаген.
Если учесть, что Дидона выбирала участок, примыкающий к берегу моря,
то задачу, стоящую перед Дидоной, можно сформулировать так: какой
формы должна быть кривая длины  , чтобы площадь фигуры,
ограниченная этой кривой и заданной линией
, чтобы площадь фигуры,
ограниченная этой кривой и заданной линией 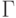 , была
наибольшей. В предположении, что
, была
наибольшей. В предположении, что  - прямая линия, решением
задачи является полуокружность длины
- прямая линия, решением
задачи является полуокружность длины  .
.
Неравенство Коши
Решение частного случая задачи Дидоны, когда требуется определить, какой из прямоугольников заданного периметра имеет наибольшую площадь, было известно еще математикам Древней Греции. Более того, эта геометрическая задача считается самой древней задачей на экстремум. Решение этой задачи приведено в VI книге "Начал" Евклида, где доказывается, что если рассмотреть прямоугольник и квадрат одного и того же периметра, то площадь квадрата будет больше площади прямоугольника.
Решение задачи Дидоны для прямоугольников и некоторых других
частных случаев этой задачи легко получить с помощью неравенства Коши, которое устанавливает, что среднее
арифметическое  неотрицательных чисел не меньше их
среднего геометрического:
неотрицательных чисел не меньше их
среднего геометрического:
![\frac{x_1+x_2+\ldots +x_n}{n}\geq \sqrt[n]{x_1 x_2\ldots
x_n},\quad x_{i}\geq 0,\quad i=\overline{1,n} .](/sites/default/files/tex_cache/de602421c1dd1a1497f23833d7485aac.png)
Равенство достигается только при 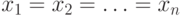 .
.
Доказательство неравенства Коши в общем виде занимает много места,
поэтому здесь мы
приведем доказательство этого неравенства только при 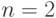 :
:
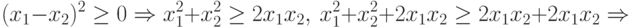
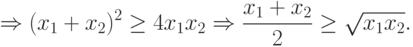
Покажем теперь на примерах, как неравенство Коши может быть использовано для решения оптимизационных геометрических задач.
Пример 1 (задача Дидоны для прямоугольников). Найдем длины сторон прямоугольника с периметром  , имеющего
наибольшую площадь.
, имеющего
наибольшую площадь.
Обозначим длины сторон прямоугольника через  и
и 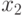 , а его площадь - через
, а его площадь - через  . Тогда
математическая модель задачи примет вид:
. Тогда
математическая модель задачи примет вид:
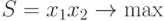
при ограничениях:
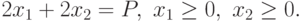
Воспользуемся неравенством Коши при 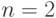 :
:
 |
( 1) |
Поскольку 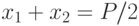 , то из (1) следует:
, то из (1) следует:
 |
( 2) |
Неравенство (2) обращается в равенство при 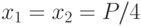 . Таким образом, прямоугольником наибольшей площади,
имеющим заданный периметр
. Таким образом, прямоугольником наибольшей площади,
имеющим заданный периметр  , является квадрат, длина стороны которого равна
, является квадрат, длина стороны которого равна  .
.
Пример 2 (обратная задача Дидоны для прямоугольников). Найдем длины сторон прямоугольника с площадью 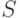 , имеющего наименьший периметр.
, имеющего наименьший периметр.
Используем обозначения, введенные в примере 1. Тогда математическая модель задачи примет вид:
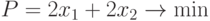
при ограничениях:
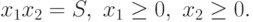
Из неравенства (1) вытекает, что
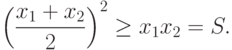
Следовательно,  . Это неравенство
обращается в равенство при
. Это неравенство
обращается в равенство при 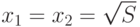 . Таким образом, прямоугольником
наименьшего периметра, имеющим заданную площадь
. Таким образом, прямоугольником
наименьшего периметра, имеющим заданную площадь 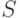 , является
квадрат, длина стороны которого равна
, является
квадрат, длина стороны которого равна  .
.
Пример 3 (задача Дидоны для параллелепипедов). Площадь поверхности параллелепипеда равна 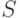 . Определим, при каких длинах сторон его объем будет максимальным.
. Определим, при каких длинах сторон его объем будет максимальным.
Обозначим длины сторон параллелепипеда через  ,
, 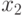 и
и  , а его объем - через
, а его объем - через 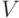 . Тогда
математическая модель задачи примет вид:
. Тогда
математическая модель задачи примет вид:
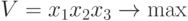
при ограничениях:
 |
( 3) |

Воспользуемся неравенством Коши при 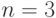 для чисел
для чисел 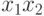 ,
, 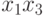 и
и 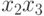 :
:
![\frac{x_1 x_2 + x_1 x_3 + x_2 x_3}{3}\geq \sqrt[3]{(x_1 x_2
x_3)^2}\ .](/sites/default/files/tex_cache/0dcd81a8c2e0c7c282cdb327375e920e.png) |
( 4) |
Неравенство (4) обращается в равенство при 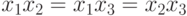 ,
откуда следует:
,
откуда следует: 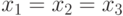 . Из (3) имеем:
. Из (3) имеем:  . При этом максимальный объем
. При этом максимальный объем
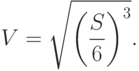
Таким образом, параллелепипед
максимального объема с площадью поверхности 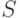 имеет
форму куба со стороной
имеет
форму куба со стороной  . Аналогично
можно показать, что параллелепипед
объема
. Аналогично
можно показать, что параллелепипед
объема 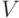 c минимальной площадью поверхности имеет
форму куба.
c минимальной площадью поверхности имеет
форму куба.
Пример 4 (задача Дидоны для треугольников). Найдем длины сторон треугольника с периметром  , имеющего наибольшую площадь.
, имеющего наибольшую площадь.
Обозначим длины сторон треугольника через  ,
, 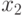 и
и  . Площадь треугольника
. Площадь треугольника  вычислим по формуле Герона. Математическая модель задачи примет вид
вычислим по формуле Герона. Математическая модель задачи примет вид
 |
( 5) |
при ограничениях:
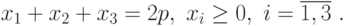 |
( 6) |
Воспользуемся неравенством Коши при 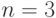 для чисел
для чисел  ,
,  ,
,  :
:
![\sqrt[3]{(p - x_1)(p - x_2)(p - x_3)}\leq \frac{p}{3}\ .](/sites/default/files/tex_cache/e1f8037aca188c3f816e43786af42c06.png)
Отсюда следует
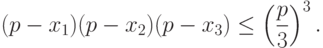 |
( 7) |
Из (5) получим
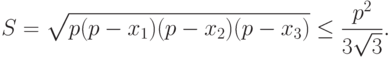
Неравенство (13) обращается в равенство при 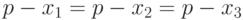 , т. е. при условии
, т. е. при условии 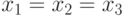 .
Из (6) получим
.
Из (6) получим

Таким образом, треугольником с периметром  , имеющим
наибольшую площадь, является равносторонний треугольник со стороной
, имеющим
наибольшую площадь, является равносторонний треугольник со стороной 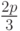 .
.
При решении более сложных задач применяется также геометрическое неравенство или обобщенное неравенство Коши, которое непосредственно связано с двойственностью в ГП (см. лекцию 4):
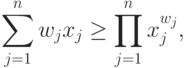 |
( 8) |
при



Используя неравенство (8), можно доказать две теоремы, которые широко применяются для оценивания нелинейных функций.
Теорема 1 Решением экстремальной задачи
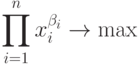
при ограничениях
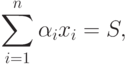

где

является вектор 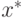 с компонентами
с компонентами
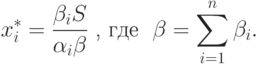 |
( 9) |
Максимальное значение целевой функции 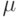 вычисляется по формуле
вычисляется по формуле
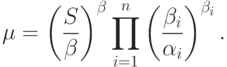 |
( 10) |
Прежде, чем привести следующий пример, поясним постановку прикладной задачи, которая в нем рассматривается.
В экономике широко применяются функции, выражающие технологическую зависимость между результатами деятельности производственного объекта и затратами факторов производства. Такие функции называются производственными функциями. Во многих экономических моделях используется производственная функция Кобба-Дугласа, которая задается формулой:

где  - объем выпускаемого продукта,
- объем выпускаемого продукта,
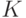 - затраты на капитальные ресурсы при производстве этого продукта.
- затраты на капитальные ресурсы при производстве этого продукта.
Пример 5 Пусть зависимость выпуска продукта от ресурсов имеет вид производственной функции Кобба-Дугласа:
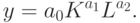
Заданы цены ресурсов  и
и 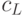 и общий объем
средств
и общий объем
средств  на выпуск продукции. Определим
объемы ресурсов
на выпуск продукции. Определим
объемы ресурсов 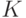 и
и 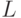 , при которых выпуск продукции максимален.
, при которых выпуск продукции максимален.
Математическая модель задачи может быть записана следующим образом:
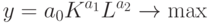
при ограничениях
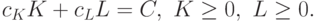
Для решения этой задачи применим теорему 1 при 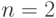 ,
, 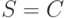 ,
,  ,
,  ,
, 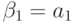 ,
, 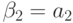 ,
,  ,
,  .
.
Оптимальные количества потребляемых ресурсов 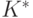 и
и 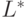 вычисляются по формулам (9):
вычисляются по формулам (9):
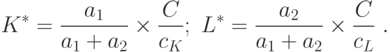
Максимальный выпуск продукции  вычисляется по формуле
(10):
вычисляется по формуле
(10):

Приведем теперь теорему, в которой речь идет об обратной задаче (см. [1]).

 - положительные
- положительные