НОУ ИНТУИТ | Введение в геометрическое программирование. Лекция 6: Преобразование некоторых задач оптимизации в задачи ГП

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Санкт-Петербургский государственный университет

Опубликован: 08.06.2009 | Доступ: свободный | Студентов: 662 / 131 | Оценка: 4.65 / 4.35 | Длительность: 07:44:00

Специальности: Программист

Теги: beta, базисными векторами, безопасность, вычисления, двойственная задача, задача линейного программирования, книги, линейное программирование, модель задач, обобщенный полином, оптимальное решение задачи, поддержка, программирование, рабочая книга, свойства множества, теория, форматы, число независимости

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В лекции описываются методы преобразования некоторых классов задач оптимизации в задачи ГП. Рассматривается аппроксимация обратных задач ГП прямыми задачами ГП и преобразование знакопеременных задач ГП в обратные задачи ГП.

Ключевые слова: класс, задача линейного программирования, условное или, аппроксимация, доказательство, вектор, связь, минимум, двойственная задача, определение, обобщенный полином, коэффициенты, полином, разность, функция, переменная, прямой

Читателю, который ознакомился с изложенным ранее материалом о задачах ГП, может показаться, что только немногие задачи оптимизации могут быть сформулированы как задачи ГП. Однако это не так. С помощью несложных преобразований довольно много задач оптимизации можно свести к эквивалентным задачам ГП. Еще больше класс задач, для которых можно указать хорошо аппроксимирующую их задачу ГП.

В учебной литературе, посвященной ГП, часто излагается процедура сведения задачи линейного программирования к эквивалентной задаче ГП (см., например, [5]). Мы не будем приводить здесь этот материал, так как он полезен только как упражнение на выполнение несложных математических преобразований. Вряд ли кто посоветует решать задачи линейного программирования посредством такого сведения.

Напомним постановку канонической задачи ГП из предыдущей лекции

$\mbox{Задача GP:}\qquad g_{0}(x)\rightarrow \min$

( 69)

при ограничениях

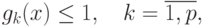$g_{k}(x)\leq 1,\quad k = \overline{1,p},$

( 70)

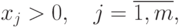
$x_{j}> 0 ,\quad j= \overline{1,m},$

где

$g_{k}(x)=\sum\limits_{i\in [k]}c_{i}\prod\limits_{j=1}^{m}{x_{j}}^{a_{ij}},\quad k= \overline{0,p},\quad c_{i}>0,\ a_{ij}\in \mathbb{R}.$

Рассмотрим сначала наиболее простые случаи преобразования задач оптимизации в задачи ГП.

Простейшие случаи преобразования

Положительная константа в правой части ограничения.
Если имеется ограничение вида

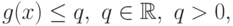
$g(x)\leq q,\ q\in \mathbb{R},\ q > 0,$

то эквивалентное ограничение имеет вид:

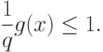
$\frac{1}{q} g(x) \leq 1.$ ( 71)

Рассмотрим пример.

Пример 37 Преобразуем ограничение

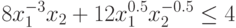
$8 x_{1}^{-3}x_{2}+12 x_{1}^{0.5}x_{2}^{-0.5}\leq 4$

в ограничение вида (70).

Используя преобразование (71), получим ограничение

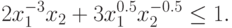
$2 x_{1}^{-3}x_{2}+3 x_{1}^{0.5}x_{2}^{-0.5}\leq 1.$
Моном в правой части ограничения.
Если имеется ограничение вида

$g(x)\leq u(x),$

где 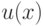- моном, то эквивалентное ограничение имеет вид: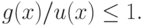

$g(x)/u(x) \leq 1.$ ( 72)

Заметим, что - позином, если является позиномом, и - моном, если является мономом. Рассмотрим пример.

Пример 38 Преобразуем ограничение

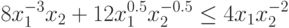
$8 x_{1}^{-3}x_{2}+12 x_{1}^{0.5}x_{2}^{-0.5}\leq 4 x_{1}x_{2}^{-2}$

в ограничение вида (70).

Используя преобразование (72), получим ограничение

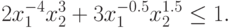
$2 x_{1}^{-4}x_{2}^{3}+3 x_{1}^{-0.5}x_{2}^{1.5}\leq 1.$
Максимизация монома.
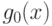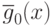Нахождение максимума (условного или безусловного) монома $g_{0}(x)$ эквивалентно нахождению минимума монома $\overline{g}_{0}(x)$ :

$\overline{g}_{0}(x) = \frac{1}{g_{0}(x)} =\frac{1}{c_{1}}\prod\limits_{j=1}^{m}{x_{j}}^{-a_{ij}},\quad c_{1}>0,\ a_{ij}\in \mathbb{R}.$ ( 73)

Рассмотрим пример.

Пример 39 Преобразуем задачу с целевой функцией

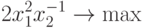
$2 x_{1}^{2}x_{2}^{-1}\rightarrow\max$

в задачу с целевой функцией вида (69).

Используя преобразование (73), получим эквивалентную задачу:

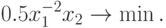
$0.5 x_{1}^{-2}x_{2}\rightarrow\min.$
Обратное ограничение на моном.
Если имеется ограничение вида

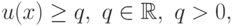
$u(x)\geq q, \ q\in \mathbb{R},\ q > 0,$

где 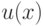- моном, то эквивалентное ограничение имеет вид: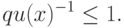

$q u(x)^{-1} \leq 1.$ ( 74)

Рассмотрим пример.

Пример 40 Преобразуем ограничение

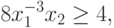
$8 x_{1}^{-3}x_{2}\geq 4,$

в ограничение вида (70).

Используя преобразование (74), получим ограничение

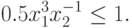
$0. 5 x_{1}^{3}x_{2}^{-1}\leq 1.$
Преобразования, использующие дополнительные переменные.
В этом пункте мы рассмотрим только частный случай преобразования, использующего дополнительные переменные. Однако сама схема преобразования носит весьма общий характер. Пусть имеется задача:

$g_{0}(x)={\frac{[h_{1}(x)]^{\alpha}}{[h_{2}(x)-h_{3}(x)]^{\beta}}}\rightarrow\min,$ ( 75)

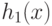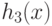где $h_{1}(x)$ , $h_{3}(x)$ - позиномы, 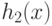$h_{2}(x)$ - моном, 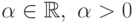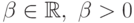$\alpha \in \mathbb{R},\ \alpha>0$ , $\beta\in \mathbb{R},\ \beta >0$ . Предполагается, что функция $[h_{2}(x)-h_{3}(x)]> 0$ , .

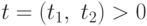Введем вектор дополнительных переменныx $t=(t_{1},\ t_{2})>0$ , такой что выполняются неравенства

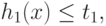
$h_{1}(x)\leq t_{1},$

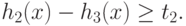
$h_{2}(x)-h_{3}(x)\geq t_{2}.$

Тогда выполняется неравенство

${\frac{[h_{1}(x)]^{\alpha}}{[h_{2}(x)-h_{3}(x)]^{\beta}}}\leq \frac{t_{1}^{\alpha}}{t_{2}^{\beta}} = t_{1}^{\alpha}t_{2}^{-\beta},$

и задача (75) эквивалентна задаче

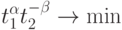
$t_{1}^{\alpha}t_{2}^{-\beta}\rightarrow\min$ ( 76)

при ограничениях

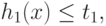
$h_{1}(x)\leq t_{1},$ ( 77)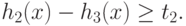

$h_{2}(x)-h_{3}(x)\geq t_{2}.$ ( 78)

Теперь, используя описанные в предыдущих пунктах преобразования, приведем задачу (76)--(78) к задаче ГП в канонической форме. Применив преобразование (72) к ограничению (77), получим ограничение

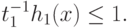
$t_{1}^{-1}h_{1}(x)\leq 1.$

Перепишем неравенство (78) в виде

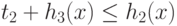
$t_{2}+h_{3}(x)\leq h_{2}(x)$

и применим преобразование (72). Получим ограничение

$t_{2}{h_{2}(x)}^{-1}+h_{3}(x){h_{2}(x)}^{-1}\leq 1.$

Таким образом получили задачу GP:

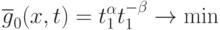
$\overline{g}_{0}(x, t)=t_{1}^{\alpha}t_{1}^{-\beta}\rightarrow\min$

при ограничениях

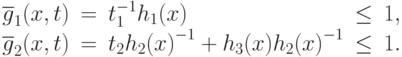
$\begin{array}{rclcr} \overline{g}_{1}(x, t)&=&t_{1}^{-1}h_{1}(x)&\leq& 1, \\ \overline{g}_{2}(x, t)&=&t_{2}{h_{2}(x)}^{-1}+h_{3}(x){h_{2}(x)}^{-1}&\leq& 1. \end{array}$

Отметим, что при использовании преобразований, описанных выше, размерность задачи увеличивается на две переменные, при этом появляются два дополнительных ограничения.

Рассмотрим пример.

Пример 41 Преобразуем задачу

${\frac{[2 x_{1}^{2}x_{2}^{-1}+x_{1}^{-2}+x_{2}^{3}]^{5}}{[3 x_{1}x_{2}^{3} - (x_{1}^{-2}+x_{2}^{2})]^{4}}}\rightarrow\min,$

при ограничениях

$x_{1}^{-1}\leq 1,$

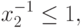
$x_{2}^{-1}\leq 1,$

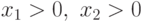
$x_{1}>0,\ x_{2}>0$

в задачу GP.

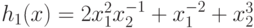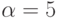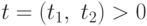Введем следующие обозначения: $h_{1}(x) = 2 x_{1}^{2}x_{2}^{-1}+x_{1}^{-2}+x_{2}^{3}$ , $h_{2}(x)=3 x_{1}x_{2}^{3}$ , $h_{3}(x) = x_{1}^{-2}+x_{2}^{2}$ , $\alpha = 5$ , $\beta=4$ . Тогда целевая функция примет вид, задаваемый формулой (75). Выполним преобразования, предложенные для этого случая. Введем вектор дополнительных переменныx $t=(t_{1},\ t_{2})>0$ , для которого выполняются неравенства: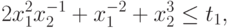
$2 x_{1}^{2}x_{2}^{-1}+x_{1}^{-2}+x_{2}^{3}\leq t_{1},$

$3 x_{1}x_{2}^{3} -(x_{1}^{-2}+x_{2}^{2})\geq t_{2}.$

Выполнив элементарные преобразования, получим следующую задачу GP:

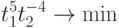
$t_{1}^{5}t_{2}^{-4}\rightarrow\min$

при ограничениях

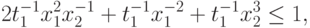
$2 t_{1}^{-1}x_{1}^{2}x_{2}^{-1}+t_{1}^{-1}x_{1}^{-2}+t_{1}^{-1}x_{2}^{3}\leq 1,$

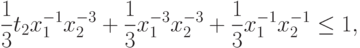
$\frac{1}{3} t_{2}x_{1}^{-1}x_{2}^{-3}+ \frac{1}{3} x_{1}^{-3}x_{2}^{-3}+ \frac{1}{3} x_{1}^{-1}x_{2}^{-1}\leq 1,$

$x_{1}^{-1}\leq 1,$

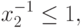
$x_{2}^{-1}\leq 1,$

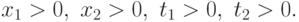
$x_{1}>0,\ x_{2}>0,\ t_{1}>0,\ t_{2}>0.$

Заметим, что исходная задача была от двух переменных и имела два ограничения (не считая ограничения на знак переменных), полученная задача ГП является задачей от четырех переменных и имеет четыре ограничения (не считая ограничения на знак переменных).