|
Так это же динамическое программирование на основе математической индукции. |
Преобразование некоторых задач оптимизации в задачи ГП
Обратная задача ГП
Обратной задачей геометрического программирования называется следующая задача:

при ограничениях
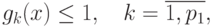 |
( 79) |
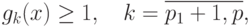 |
( 80) |
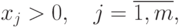
где
![g_{k}(x)=\sum\limits_{i\in
[k]}c_{i}\prod\limits_{j=1}^{m}{x_{j}}^{a_{ij}},\quad
k= \overline{0,p},\quad c_{i}>0,\ a_{ij}\in \mathbb{R}.](/sites/default/files/tex_cache/666d87e114b32fb1580251e98d9c31d1.png) |
( 81) |
Обратная задача ГП отличается от задачи GP наличием ограничений вида (80), которые называются обратными ограничениями.
Покажем, что обратную задачу ГП можно аппроксимировать двумя семействами задач ГП. Аппроксимация базируется на неравенствах, связывающих арифметические и гармонические средние. Эти неравенства приведены в лемме, доказательство которой можно найти, например, в [5].
Лемма 1 Для положительных чисел 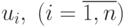 и
положительных чисел
и
положительных чисел 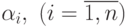 ,
удовлетворяющих условию
,
удовлетворяющих условию
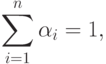
выполняются неравенства
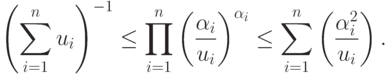
Эти неравенства превращаются в равенства тогда и только тогда, когда
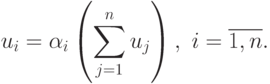
Введем определения. Геометрическим обратным мономом 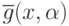 для позинома
для позинома
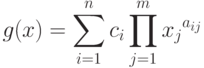
называется моном вида
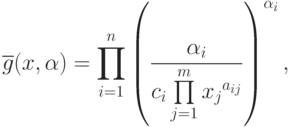 |
( 82) |
где положительные веса 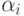 ,
,  ,
удовлетворяют условию
,
удовлетворяют условию 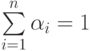 .
.
Гармоническим обратным позиномом 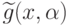 для
позинома
для
позинома  называется позином вида
называется позином вида
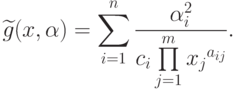 |
( 83) |
где положительные веса 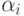 ,
,  ,
удовлетворяют условию
,
удовлетворяют условию 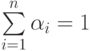 .
.
Из леммы 1 следует, что, если положить 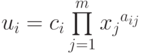 ,
то для любого
,
то для любого  выполняются неравенства:
выполняются неравенства:
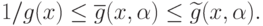 |
( 84) |
Введем в рассмотрение семейство сжатых задач  для задачи IGP, в которых обратные ограничения заменены
ограничениями вида
для задачи IGP, в которых обратные ограничения заменены
ограничениями вида 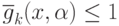 :
:
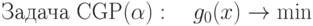
при ограничениях
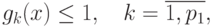
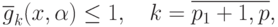
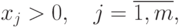
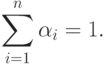
где 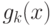 - позиномы вида (81),
- позиномы вида (81), 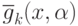 - мономы вида
(82). Каждой задаче из семейства соответствует вектор весов
- мономы вида
(82). Каждой задаче из семейства соответствует вектор весов  ,
который удовлетворяет условиям
,
который удовлетворяет условиям
![\sum\limits_{i\in [k]}\alpha_{i} = 1, \quad k = \overline{p_1+1, p}.](/sites/default/files/tex_cache/8d3595c58199f6fb2432cd3e65fe7e70.png)
Задачи из семейства  являются задачами ГП.
Связь между обратной задачей ГП и соответстующим семейством
сжатых задач
являются задачами ГП.
Связь между обратной задачей ГП и соответстующим семейством
сжатых задач  сформулируем в виде теоремы.
сформулируем в виде теоремы.
Теорема 12 Оптимальное решение 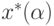 любой сжатой задачи из семейства
любой сжатой задачи из семейства  является допустимым решением соответствующей обратной задачи IGP.
Если обратная задача IGP имеет оптимальное решение
является допустимым решением соответствующей обратной задачи IGP.
Если обратная задача IGP имеет оптимальное решение 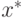 , то
существует вектор весов
, то
существует вектор весов 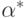 ,
при котором
,
при котором 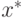 является оптимальным решением сжатой задачи,
соответсвующей этому вектору весов.
является оптимальным решением сжатой задачи,
соответсвующей этому вектору весов.
Доказательство. Обозначим через 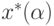 оптимальное решение
задачи из семейства
оптимальное решение
задачи из семейства  при векторе весов
при векторе весов  .
Так как оптимальное решение
.
Так как оптимальное решение 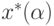 является допустимым решением задачи, то для него
выполнены неравенства
является допустимым решением задачи, то для него
выполнены неравенства
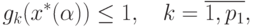
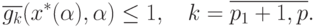
Тогда из неравенства (84) следует, что выполнены неравенства
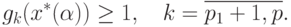
Следовательно, 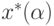 является допустимым решением задачи IGP.
является допустимым решением задачи IGP.
Пусть задача IGP имеет оптимальное решение. Обозначим его через 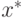 .
Покажем, что существует вектор весов
.
Покажем, что существует вектор весов 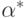 такой, что для соответствующей ему
задачи вектор
такой, что для соответствующей ему
задачи вектор 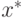 будет допустимым решением. Введем следующие обозначения:
будет допустимым решением. Введем следующие обозначения:
![\beta_k=g_k(x^*)=\sum\limits_{i\in [k]}u_i^* \leq 1, \quad k = \overline{p_1+1, p}.](/sites/default/files/tex_cache/45ad41c32577cdaa69654a0f3aafb9fd.png)
![\alpha^*_i = \frac{u_i^*}{\beta_k},\ i\in [k], \quad k = \overline{p_1+1, p}](/sites/default/files/tex_cache/11fa5d04180592aee01753bac637d477.png)
является вектором весов, а 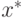 - допустимым (и оптимальным) решением соответствующей ему сжатой задачи:
- допустимым (и оптимальным) решением соответствующей ему сжатой задачи:
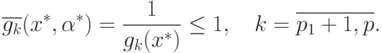
Приведем пример на построение семейства сжатых задач.
Пример 42 Образуем для обратной задачи ГП

при ограничениях
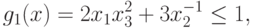
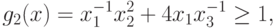 |
( 85) |
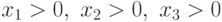
семейство сжатых задач.
Заменим обратное ограничение (85) прямым. Для этого
вычислим геометрическое обратное для позинома 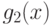 по
формуле (82):
по
формуле (82):
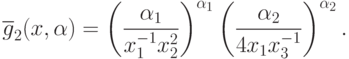
Упростим последнюю формулу:
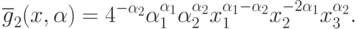
Таким образом, семейство сжатых задач для рассматриваемой задачи имеет вид

при ограничениях
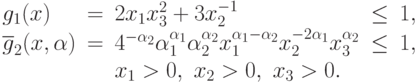
Задачи ГП из этого семейства отличаются только видом второго
ограничения (на значения позинома 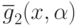 ).
Например, при
).
Например, при 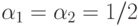 это ограничение будет
иметь вид:
это ограничение будет
иметь вид:
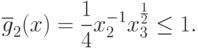
Из (84) следует, что минимум 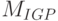 задачи
задачи  и минимум
и минимум 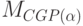 задачи
задачи  связаны соотношением
связаны соотношением

Таким образом, можно решить задачу  для
некоторых весов
для
некоторых весов 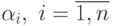 и полученное
решение будет оценкой сверху для обратной задачи
и полученное
решение будет оценкой сверху для обратной задачи  .
.
Введем в рассмотрение семейство гармонических задач 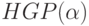 для задачи IGP, в которых обратные
ограничения заменены ограничениями вида
для задачи IGP, в которых обратные
ограничения заменены ограничениями вида 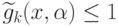 :
:
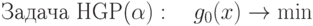
при ограничениях
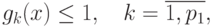
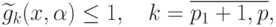
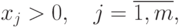
где 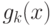 - позиномы вида (81),
- позиномы вида (81), 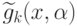 - позиномы вида
(83).
- позиномы вида
(83).
Каждой задаче из семейства соответствует вектор весов  ,
который удовлетворяет условиям
,
который удовлетворяет условиям
![\sum\limits_{i\in [k]}\alpha_{i} = 1, \quad k = \overline{p_1+1, p}.](/sites/default/files/tex_cache/8d3595c58199f6fb2432cd3e65fe7e70.png)
Задачи из семейства 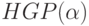 являются задачами ГП.
Связь между обратной задачей ГП и соответстующим семейством
гармонических задач
являются задачами ГП.
Связь между обратной задачей ГП и соответстующим семейством
гармонических задач 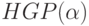 сформулируем в виде
теоремы.
сформулируем в виде
теоремы.
Теорема 13 Оптимальное решение 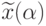 любой гармонической
задачи из семейства
любой гармонической
задачи из семейства 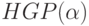 является допустимым
решением соответствующей обратной задачи IGP. Если обратная
задача IGP имеет оптимальное решение
является допустимым
решением соответствующей обратной задачи IGP. Если обратная
задача IGP имеет оптимальное решение 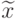 , то
существует вектор весов
, то
существует вектор весов  , при котором
, при котором 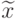 является оптимальным решением гармонической
задачи, соответсвующей этому вектору весов.
является оптимальным решением гармонической
задачи, соответсвующей этому вектору весов.
Доказательство этой теоремы аналогично доказательству теоремы 12.
Приведем пример на построение семейства гармонических задач.
Пример 43 Образуем для обратной задачи ГП

при ограничениях
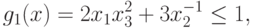
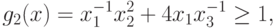 |
( 86) |
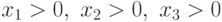
семейство гармонических задач.
Заменим обратное ограничение (86) прямым. Для этого
вычислим гармоническое обратное для позинома 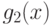 по
формуле (83):
по
формуле (83):

Упростим последнюю формулу:

Таким образом, семейство гармонических задач для рассматриваемой задачи имеет вид

при ограничениях
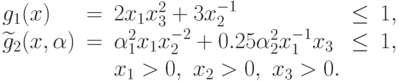
Задачи ГП из этого семейства отличаются только видом второго
ограничения (на значения позинома 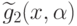 ). Например, при
). Например, при 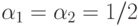 это
ограничение будет иметь вид:
это
ограничение будет иметь вид:
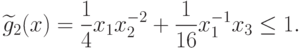
Из (84) следует, что минимум 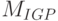 задачи
задачи  и
минимум
и
минимум 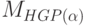 задачи
задачи 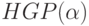 связаны соотношением
связаны соотношением

Таким образом, можно решить задачу 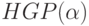 для
некоторых весов
для
некоторых весов 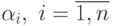 и полученное
решение будет оценкой сверху для обратной задачи
и полученное
решение будет оценкой сверху для обратной задачи  .
.
На данный момент нет достаточной вычислительной практики, которая показывала бы, какая аппроксимация эффективнее. Однако отметим, что двойственные задачи для семейства сжатых задач имеют меньше двойственных переменных по сравнению с гармоническими задачами, поскольку геометрическое обратное является мономом. Это облегчает решение задачи двойственными методами.
