|
Так это же динамическое программирование на основе математической индукции. |
Преобразование некоторых задач оптимизации в задачи ГП
Оценивание знакопеременных задач с позиномами
В этом разделе будет показано, как можно свести задачу ГП с ограничениями на знакопеременные полиномы к обратной задаче ГП.
Введем определение. Знакопеременным полиномом (сигномом) называется (обобщенный) полином
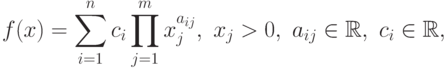 |
( 87) |
который отличается от позинома тем, что коэффициенты  могут
быть отрицательными. Члены знакопеременного полинома удобно
располагать так, чтобы первыми в сумме стояли члены с
положительными коэффициентами
могут
быть отрицательными. Члены знакопеременного полинома удобно
располагать так, чтобы первыми в сумме стояли члены с
положительными коэффициентами  (если такие имеются).
(если такие имеются).
Рассмотрим преобразование ограничений на знакопеременные полиномы в ограничения на позиномы, описанное, например, в [5].
Ясно, что любой знакопеременный полином представляет собой либо позином, либо позином, взятый со знаком минус, либо разность двух позиномов. Любое ограничение на знакопеременный полином может быть представлено в одном из трех видов:
 |
( 88) |
Если целевая функция является сигномом, то сначала ее надо
преобразовать путем введения новой положительной дополнительной
переменной, появится дополнительное ограничение. Опустим это
преобразование, предположив, что рассматривается задача, у которой
целевая функция - позином. Итак, пусть требуется
минимизировать позином  при ограничениях на
знакопеременные полиномы:
при ограничениях на
знакопеременные полиномы:
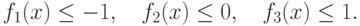
Если  - позином, то ограничение
- позином, то ограничение 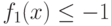 не
может быть удовлетворено, следовательно, задача несовместна
(противоречива). Если
не
может быть удовлетворено, следовательно, задача несовместна
(противоречива). Если  - позином с отрицательным знаком,
то это ограничение эквивалентно ограничению
- позином с отрицательным знаком,
то это ограничение эквивалентно ограничению  ,
которое имеет второй из требуемых видов, указанных в
(88), следовательно, остается рассмотреть случай, когда
,
которое имеет второй из требуемых видов, указанных в
(88), следовательно, остается рассмотреть случай, когда  представляет собой разность двух позиномов.
представляет собой разность двух позиномов.
Если 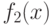 - позином, то ограничение
- позином, то ограничение  не может
быть удовлетворено, следовательно, задача несовместна
(противоречива). Если
не может
быть удовлетворено, следовательно, задача несовместна
(противоречива). Если 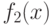 - позином с отрицательным знаком,
то это ограничение удовлетворяется автоматически и может быть
исключено из рассмотрения, следовательно, остается рассмотреть
случай, когда
- позином с отрицательным знаком,
то это ограничение удовлетворяется автоматически и может быть
исключено из рассмотрения, следовательно, остается рассмотреть
случай, когда 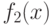 представляет собой разность двух позиномов.
представляет собой разность двух позиномов.
Если  - позином, то ограничение
- позином, то ограничение 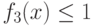 имеет
первый из требуемых видов, указанных в (88). Если
имеет
первый из требуемых видов, указанных в (88). Если 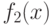 - позином с отрицательным знаком, то это ограничение
удовлетворяется автоматически и может быть опущено, следовательно,
остается рассмотреть случай, когда
- позином с отрицательным знаком, то это ограничение
удовлетворяется автоматически и может быть опущено, следовательно,
остается рассмотреть случай, когда  представляет собой
разность двух позиномов.
представляет собой
разность двух позиномов.
Таким образом, предположим, что нужно минимизировать позином  при ограничениях
при ограничениях
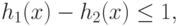 |
( 89) |
 |
( 90) |
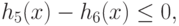 |
( 91) |
где  - позиномы,
- позиномы,  .
.
Введем дополнительный вектор 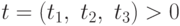 . Вектор
. Вектор  является допустимым решением этих ограничений тогда и только
тогда, когда имеются положительные значения для
является допустимым решением этих ограничений тогда и только
тогда, когда имеются положительные значения для 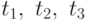 такие, что дополненный вектор
такие, что дополненный вектор  является
допустимым решением, удовлетворяющим ограничениям
является
допустимым решением, удовлетворяющим ограничениям

следовательно, получим шесть ограничений:
 |
( 92) |
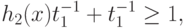 |
( 93) |
 |
( 94) |
 |
( 95) |
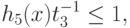 |
( 96) |
 |
( 97) |
Таким образом, получили обратную задачу ГП:
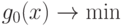
при ограничениях
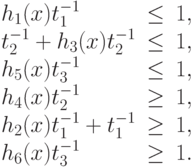
Рассмотрим пример.
Пример 44 Преобразуем задачу с ограничениями на сигномы вида

при ограничениях
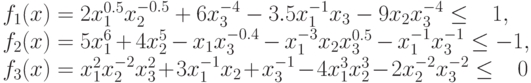
в обратную задачу ГП.
Ограничение на сигном 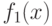 имеет вид (89), здесь
имеет вид (89), здесь 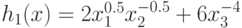 ,
, 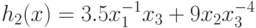 .
Ограничение на
.
Ограничение на 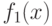 порождает два ограничения вида
(92) и (93):
порождает два ограничения вида
(92) и (93):
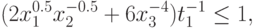
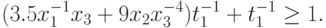
Здесь 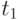 - положительная дополнительная переменная, такая,
что выполняются неравенства:
- положительная дополнительная переменная, такая,
что выполняются неравенства:

Ограничение на сигном  имеет вид (90), здесь
имеет вид (90), здесь 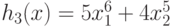 ,
,  .
Ограничение на
.
Ограничение на  порождает два ограничения вида
(94) и (95):
порождает два ограничения вида
(94) и (95):
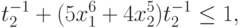

Здесь 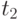 - положительная дополнительная переменная, такая,
что выполняются неравенства:
- положительная дополнительная переменная, такая,
что выполняются неравенства:
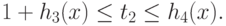
Ограничение на сигном 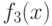 имеет вид (91), здесь
имеет вид (91), здесь 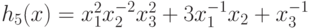 ,
,  .
Ограничение на
.
Ограничение на 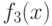 порождает два ограничения вида
(96) и (97):
порождает два ограничения вида
(96) и (97):


Здесь 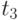 - положительная дополнительная переменная, такая,
что выполняются неравенства:
- положительная дополнительная переменная, такая,
что выполняются неравенства:
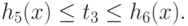
Таким образом, получили обратную задачу ГП:

при ограничениях
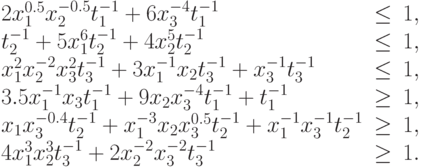
Обратную задачу ГП можно аппроксимировать прямой задачей ГП при помощи преобразований, описанных в предыдущем разделе.
Краткие итоги
Описаны простейшие методы преобразования определенного класса задач оптимизации в задачи ГП. Приведена постановка обратной задачи ГП. Объяснено, как можно аппроксимировать обратную задачу ГП прямой. Приведена постановка знакопеременной задачи ГП, показано, как можно преобразовать эту задачу в обратную задачу ГП.
