Стратегическое развитие проекта в условиях неопределенности и факторов риска

На практике часто появляется необходимость согласования действий фирм, объединений, министерств и других участников проектов в случаях, когда их интересы не совпадают. В таких ситуациях теория игр [14] позволяет найти лучшее решение для поведения участников, обязанных согласовывать действия при столкновении интересов. Теория игр все шире проникает в практику экономических решений и исследований. Ее можно рассматривать как инструмент, помогающий повысить эффективность плановых, маркетинговых и управленческих решений. Это имеет большое значение при решении задач в промышленности, сельском хозяйстве, на транспорте, в торговле и других отраслях народного хозяйства. Метод теории игр можно применять при выборочных обследованиях конечных товарных совокупностей, при проверке статистических гипотез и других предположений, касающихся оценки возможностей предприятий и запросов потребителей.

Обычно теорию игр определяют как раздел математики для изучения конфликтных ситуаций. Это означает, что можно выработать оптимальные правила поведения каждой стороны, участвующей в решении конфликта.

Выбор стратегий развития с помощью дерева решений (позиционные игры)

Рассмотрим более сложные (позиционные, или многоэтапные) решения в условиях риска. Одноэтапные "игры с природой", таблицы решений удобно использовать в задачах, имеющих одно множество альтернативных решений и одно множество состояний среды. Многие задачи, однако, требуют анализа последовательности решений и состояний среды, когда одна совокупность стратегий игрока и состояний природы порождает другое состояние подобного типа [ 15 ]. Если имеют место два или более последовательных множеств решений, причем последующие решения основываются на результатах предыдущих, и/или два или более множеств состояний среды (т.е. появляется целая цепочка решений, вытекающих одно из другого, которые соответствуют событиям, происходящим с некоторой вероятностью), используется дерево решений.

Дерево решений - это графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций альтернатив и состояний среды.

Процесс принятия решений с помощью дерева решений в общем случае предполагает выполнение следующих пяти этапов.

• Этап 1. Формулирование задачи. Прежде всего необходимо отбросить не относящиеся к проблеме факторы, а среди множества оставшихся выделить существенные и несущественные. Это позволит привести описание задачи принятия решения к поддающейся анализу форме. Должны быть выполнены следующие основные процедуры: определение возможностей сбора информации для экспериментирования и реальных действий; составление перечня событий, которые с определенной вероятностью могут произойти; установление временного порядка расположения событий, в исходах которых содержится полезная и доступная информация, и тех последовательных действий, которые можно предпринять.
• Этап 2. Построение дерева решений, т.е. графическое представление последовательности возможных альтернативных действий с учетом соответствующих внешних условий, начиная с "корня" и завершая "листочками".
• Этап 3. Оценка вероятностей состояний среды, т.е. сопоставление шансов возникновения каждого конкретного события. Следует отметить, что указанные вероятности определяются либо на основании имеющейся статистики, либо экспертным путем.
• Этап 4. Установление выигрышей (или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации альтернатив (действий) и состояний среды.
• Этап 5. Решение задачи, состоящее в определении на дереве решений "веточки", для которой установленный на этапе 4 выигрыш является максимальным.

Прежде чем продемонстрировать процедуру применения дерева решений, введем ряд определений. В зависимости от отношения к риску решение задачи может выполняться с позиций так называемых "объективистов" и "субъективистов".

Поясним эти понятия на следующем примере.

Пусть предлагается лотерея: за 10 руб. (стоимость лотерейного билета) игрок c равной вероятностью p=0,5 может ничего не выиграть или выиграть 100 руб. Один индивид пожалеет и 10 руб. за право участия в такой лотерее, т.е. просто не купит лотерейный билет, другой готов заплатить за лотерейный билет 50 руб., а третий заплатит даже 60 руб. за возможность получить 100 руб. (например, когда ситуация складывается так, что, игрок может достичь своей цели, только имея 100 руб., поэтому возможная потеря последних денежных средств, а у него их ровно 60 руб., не меняет для него ситуации).

Безусловным денежным эквивалентом (БДЭ) игры называется максимальная сумма денег, которую лицо, принимающее решение (ЛПР) готов заплатить за участие в игре (лотерее), или, что то же, та минимальная сумма денег, за которую он готов отказаться от игры. Каждый индивид имеет свой БДЭ.

Индивида, для которого БДЭ совпадает с ожидаемой денежной оценкой (ОДО) игры, т.е. со средним выигрышем в игре (лотерее), условно называют объективистом, индивида, для которого БДЭ не равно ОДО, - субъективистом. Ожидаемая денежная оценка рассчитывается как сумма произведений размеров выигрышей на вероятности этих выигрышей. Например, для нашей лотереи ОДО=0,5x0 + 0,5x100 = 50 руб. Если субъективист склонен к риску, то его БДЭ>ОДО. Если не склонен - то БДЭ<ОДО. Вопрос об отношении к риску более строго рассматривается в рамках теории Неймана-Моргенштерна [8].

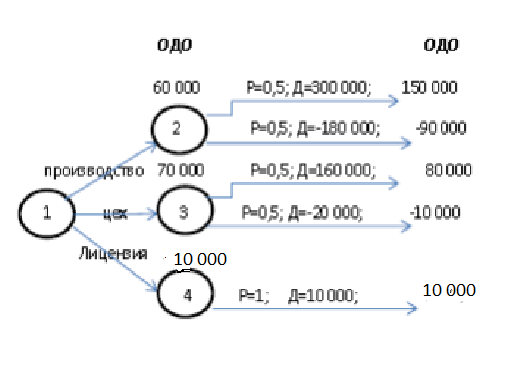
Предположим, что решения принимаются с позиции объективиста. Рассмотрим процедуру принятия решения на основе построенного дерева решения. Допустим, в действующем предприятии разработали новое устройство, которое будет востребовано на рынке. На устройство получен патент, который может быть продан за 10 000 ед. Перед автором устройства (1 на рис.5.1. ) стоит задача выбора варианта развития проекта:

• организовать собственное производство ( узел 2);
• организовать цех на действующем предприятии (узел 3);
• продать лицензию на производство устройства другому предприятию (узел 4).

Рис. 5.1. Дерево решения проекта

При организации собственного производства с равной вероятностью р=0,5 могут наступить благоприятный и неблагоприятный исходы. В случае благоприятного исхода доход предприятия может достигнуть Д = 300 000 ед., при неблагоприятном исходе предприятие потерпит убытки Д= -180 000. При этом вероятностная стоимость проекта при благоприятном исходе будет равна 150 000 ед. и -90 000 ед. при неблагоприятном. ОДО варианта 2 будет равняться сумме вероятностных исходов, связанных с этим вариантом и в нашем примере равна 60 000 ед. Аналогичные расчеты по варианту 3 дают значение ОДО = 70 000 ед. и по 4 варианту ОДО = 10 000 ед. Сравнение вероятностных стоимостей показывает, что наиболее предпочтительным следует считать вариант 2, так как он имеет максимальное значение (70 000 ед.)

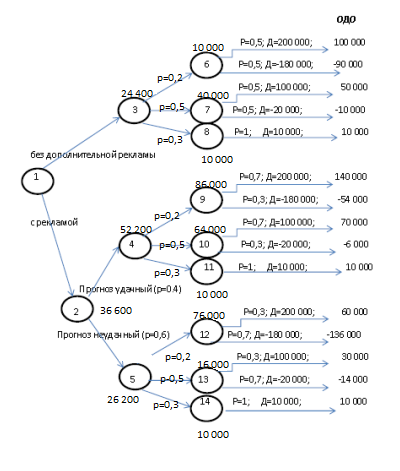
При решении задач реального бизнеса деревья решений имеют более сложную структуру, в которой учитываются все возможные состояния проекта. В качестве примера дополним рассмотренную задачу вариантом привлечения рекламной компании к распространению на том же рынке нового изделия (Рис.5.2.) К рассмотренному графу добавляются через узел 2 два аналогичных графа, один из которых соответствует благоприятному исходу (узел 4) с вероятностью р=0,4 , и узел 5 - неблагоприятному исходу с вероятностью р=0,6. В узлах 9,10 и 12, 13 ситуация может принимать благоприятное значение с вероятностью р=0,7 и неблагоприятное значение с вероятностью р=0,3. Узлы 8, 11, 14 соответствуют продаже лицензии и во всех случаях имеют одни и те же параметры. Соответствующие принятым значениям вероятностей значения ОДО представлены на рис.6.2.

Анализируя дерево решений, можно сделать следующие выводы:

• необходимо проводить рекламную кампанию, поскольку это позволяет существенно увеличить возможный доход;
• если фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно строить предприятие (ожидаемая максимальная прибыль 86 000 ед.), если прогноз неблагоприятный - организовывать производство в цеху (ожидаемая максимальная прибыль 16 000 ед.);
• на выбор решения существенное влияние оказывают задаваемые вероятности развития процессов, в связи с чем необходимо тщательно подходить к оценке этих значений на стадии проектирования и на стадии реализации проекта.

Рис. 5.2. Дерево решения проекта с участием рекламной компании

Ожидаемая ценность точной информации

Предположим, что консультационная фирма за определенную плату готова предоставить информацию о фактической ситуации на рынке в тот момент, когда руководству компании надлежит принять решение о масштабе производства. Принятие предложения зависит от соотношения между ожидаемой ценностью (результативностью) точной информации и величиной запрошенной платы за дополнительную (истинную) информацию, благодаря которой может быть откорректировано принятие решения, т.е. первоначальное действие может быть изменено.

Ожидаемая ценность точной информации о фактическом состоянии рынка равна разности между ожидаемой денежной оценкой при наличии точной информации и максимальной ожидаемой денежной оценкой при отсутствии точной информации.

Рассчитаем ожидаемую ценность точной информации для примера, в котором дополнительное обследование конъюнктуры рынка не проводится. При отсутствии точной информации, как уже было показано выше, ожидаемая денежная оценка равна:

ОДО = 24 400 руб.

Если точная информация об истинном состоянии рынка будет благоприятной (ОДО = 200 000 руб.), принимается решение строить крупное производство, если неблагоприятной, то наиболее целесообразное решение - продажа патента (ОДО = 10000 руб.). Учитывая, что вероятности благоприятной и неблагоприятной ситуаций равны 0,5, значение ОДО_т.и (ОДО точной информации) определяется выражением:

ОДО_т.и = 0,5 x 150 000 + 0,5 x 20 000 = 85 000 руб.

Тогда ожидаемая ценность точной информации равна:

ОЦ_т.и = ОДО_т.и - ОДО = 85 000 - 24 400 = 60 600 руб.

Значение ОЦ_т.и показывает, какую максимальную цену должна быть готова заплатить компания за точную информацию об истинном состоянии рынка в тот момент, когда ей это необходимо.

Резюмируя вышеизложенное, следует отметить, что наиболее обоснованные маркетинговые решения принимаются с использованием современного экономико-математического инструментария, одним из разновидностей которого является математический аппарат теории игр. В частности, в условиях неопределенности и риска эффективным методом, повышающим качество маркетинга и позволяющим оценить затраты на изучение конъюнктуры рынка, представляются исследования моделей, построенных на основе деревьев решений. Применение на практике изложенных теоретических концепций позволит получить существенный экономический результат на предприятиях широкого производственного профиля, реализующих свою продукцию самостоятельно и через посреднические организации.