Лекция 10: Арифметические операции над числами с плавающей запятой
Особенности представления чисел с плавающей запятой согласно стандарту IEEE 754
В настоящее время для представления чисел с плавающей запятой используется версия стандарта IEEE 754-2008.
Этот стандарт определяет
- формат представления двоичных и десятичных чисел с плавающей запятой;
- программные преобразования чисел с плавающей запятой при использовании различных языков программирования;
- аппаратную реализацию арифметических действий над числами с плавающей запятой.
Стандарт описывает
- как представлять нулевые числа (без наличия такой возможности представить число Z=0 в виде числа с плавающей запятой невозможно, так как нормализованная мантисса числа с плавающей запятой должна быть отлична от нуля);
- как представлять специальную величину бесконечность (Infiniti);
- как представлять специальную величину "Не число" (NaN или NaNs); к этому понятию относятся символы и результаты недопустимых операций;
- режимы округления при выполнении операций
и некоторые другие особенности работы с такими числами.
В данном разделе мы рассмотрим лишь некоторые из них, которые либо уже использовались нами при выполнении тех или иных операций, либо каким-либо образом влияют на кодирование числа в ЭВМ.
Стандарт IEEE 754 определяет четыре формата представления чисел с плавающей запятой:
- с одинарной точностью (single-precision);
- с двойной точностью (double-precision);
- с одинарной расширенной точностью (single-extended precision) >=43 бит (редко используемый);
- с двойной расширенной точностью (double-extended precision) >= 79 бит (обычно используют 80 бит).
Рассмотрим форматы, наиболее часто используемые чисел: с одинарной, двойной и двойной расширенной точностью (Рис. 10.2)
Размеры полей для чисел разных форматов представлены в Табл. 10.2.
| Точность | Одинарная single-precision | Двойная double-precision | Двойная расширенная double-extended precision |
|---|---|---|---|
| Размер (байты) | 4 | 8 | 10 |
| Поле порядка (бит) | 8 | 11 | 15 |
| Поле мантиссы (бит) | 23 | 52 | 63 |
| Наибольшее значение | 3,4×10+38 | 1,7×10+308 | 1,1×10+4932 |
| Максимальная относительная погрешность | 10-7 | 10-16 | 10-19 |
Отметим несколько моментов в машинном представлении числа с плавающей запятой. Как мы указывали ранее, число с плавающей запятой может иметь как порядок, так и мантиссу в виде числа со знаком. На Рис. 10.2 представлено поле для кодирования только одного знака. И это является знаком мантиссы, то есть знаком самого числа. Знак порядка неявно закодирован в поле самого порядка в виде так называемого смещенного, или машинного порядка:
Псм = Пx + Δ,
где Псм – смещенный порядок, закодированный в соответствующем поле числа в ячейке памяти или регистре компьютера, Пx – истинный порядок числа, значение Δ выбирается таким образом, чтобы любой смещенный порядок стал неотрицательным, то есть Δ = |-Пx|макс.
Это приводит к несколько другой схеме обработки смещенных порядков, но позволяет немного выиграть в производительности компьютера. К тому же следует иметь в виду, что для обработки порядков в компьютере используется отдельное устройство.
Еще один момент, который хотелось бы здесь отметить, связан с понятием нормализованной мантиссы, которое используется в этом ГОСТе.
Так, при обсуждении выше в этой лекции порядка и особенностей выполнения основных арифметических операций над числами с плавающей запятой и возникающих при этом особых случаях мы опирались на понятие нормализованной мантиссы в соответствии с (12.1). Согласно ГОСТ 754 мантисса двоичного числа считается нормализованной, если она удовлетворяет следующему условию:
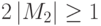 |
( 10.2) |
Т. е. модуль нормализованной мантиссы всегда имеет целую часть, равную единице.
В связи с этим нет необходимости хранить ее непосредственно в памяти, а целесообразно добавлять ее непосредственно при выполнении операции. Тогда при записи числа в поле мантиссы освобождается еще один дополнительный разряд, который используется для увеличения точности длины мантиссы и, следовательно, точности представления числа.
Операции над такими числами необходимо проводить с учетом данного обстоятельства.
В Табл. 10.3 показана связь между представлением чисел различных форматов и местом их обработки в ЭВМ.
| Тип данных | Размер, байт | Диапазон | Блок обработки |
|---|---|---|---|
| Целые без знака |
1 2 4 |
0...255 0...65535 0...4,3*109 |
АЛУ ФТ |
| Целые со знаком |
1 2 4 |
-128...+127 -32768...+32767 2,1*109...+2,1*109 |
АЛУ ФТ |
| 8 | 9,1*1018...+9*1018 | FPU | |
| С плавающей точкой |
4 (1+8+23) знак-порядок-мантисса |
±3,37*1035 | FPU |
| 8 (1+11+52) | ±1,67*10308 | ||
| 10 (1+15+64) | ±1,1*104932 | ||
| Двоично-десятичные числа |
1 распакованный 1 упакованных 10 упакованных |
0...9 0...99 0...9...9 (18 цифр) |
АЛУ ФТ АЛУ ФТ FPU |
Числа с двойной расширенной точностью используются для обработки упакованных двоично-десятичных данных в FPU (Floating Point Unit – блоке для обработки данных с плавающей точкой (запятой) микропроцессора). При этом сами данные размещаются в поле мантиссы (разряды с нулевого по 63-й), а знак числа повторяется во всех разрядах с 64-го по 79-й.
Краткие итоги
В лекции рассмотрены арифметические операции обработки чисел с плавающей запятой: алгебраическое сложение, умножение, деление. Особое внимание уделено особым ситуациям, возникающим в процессе выполнения этих операций, методам их обработки. Дано представление чисел с плавающей запятой согласно ГОСТ 754 и вытекающие из этого представления особенности хранения и обработки таких чисел.
Вопросы и задания
- Укажите формат числа с плавающей запятой. Какую характеристику числа определяет количество разрядов, отводимых под его порядок, а какую – под его мантиссу?
- Для чего требуется нормализация мантиссы числа с плавающей запятой?
- Определите минимальное количество разрядов, которое необходимо для представления числа 534,2110 с точностью 1%.
- Укажите особые случаи при умножении чисел с плавающей запятой. Каковы пути их решения? Какое устройство занимается этим?
- Укажите особые случаи при делении чисел с плавающей запятой. Каковы пути их решения?
- Каким образом при алгебраическом сложении производится денормализации мантиссы числа с меньшим порядком? При ответе учитывать, что на уровне схемотехники в распоряжении разработчика имеются регистры сдвига лишь на один разряд.
- Определите величину константы, которая используется для чисел одинарной, двойной и расширенной точности, чтобы превратить истинный порядок числа с плавающей запятой в машинный.
- Представьте число (-0,01510) в следующей разрядной двоичной сетке (1 - 3 - 5 – знак - порядок машинный - мантисса) согласно ГОСТ 754.

