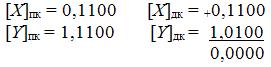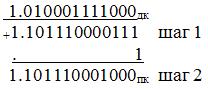Лекция 7: Способы представления чисел в ЭВМ. Сложение чисел в обратном и дополнительном кодах
Дополнительный код
Здесь связь между числом X и его изображением в дополнительном коде [Х]дк определяется следующим равенством.
Положительное число в дополнительном коде выглядит так же, как и в прямом и обратом кодах, то есть для X > 0 справедливо утверждение:
Xдк = Xпк = Xок
Получение дополнительного кода отрицательного числа осуществляется в соответствии с равенством:
[Х]дк = [2 + Х – 2-n] + 2-n = [Х]ок + 2-n
Обратное преобразование отрицательного числа (от дополнительного к прямому) выполняется следующим образом.
![\left[-0, x_1...x_n\right]_{ДК}=1,\overline{x}_1...\overline{x}_n+2^{-n}=\left[1,\overline{\overline{x}}_1...\overline{\overline{x}}_n\right]_{ДК}=1,\overline{\overline{x}}_1...\overline{\overline{x}}_n+2^{-n}=1, x_1...x_n](/sites/default/files/tex_cache/9ee9c0b3cdcded3a6c5643b595590d93.png)
Например [[- 0,1101]дк = 1,0011]дк = 1,1101, то есть от дополнительного кода берется дополнительный код.
Рассмотрим четыре случая:
- Х > 0, Y > 0, a X + Y < 1. Как и при обратном коде, суммирование дополнительных кодов не вносит каких-либо изменений в операцию сложения.
- Х > 0, Y < 0 и Х + Y > 0.
[Х]дк + [Y]дк = X + (2 + Y) = 2 + (X + Y) – предварительный результат.
Правильный результат при Х + Y > 0 равен X + Y.
Выполняется коррекция, равная вычитанию 2 из предварительного результата (исключение в нем единицы с весом 21).
Методика выполнения операции не изменяется, когда [Х]дк + [Y]дк = 0.
Например,
То есть ноль в дополнительном коде ноль имеет единственное представление.
- Х > 0, Y < 0 и Х + Y < 0.
Здесь действие
[Х]дк + [Y]дк = X + (2 + Y) = 2 + (X + Y)
дает правильный результат без коррекции.
- Х < 0, Y < 0 и |Х + Y| < 1.
[Х]дк+ [Y]дк = (2 + Х) + (2 + Y) = 2 + 2 + X + Y ,
получаем результат, который отличается от правильного
[(X + Y) < 0]дк = 2 + (X + Y) на 2.
Необходима и здесь коррекция, рассмотренная в случае 2, то есть вычитание 2 из предварительного результата (исключение в нем единицы с весом 21).
Достоинства операций суммирования чисел в обратном и дополнительном кодах:
- обработка знаковых и цифровых разрядов чисел осуществляется по одинаковым правилам, и при этом автоматически получается правильный знак результата;
- исключена операция прямого вычитания.
Недостаток: невозможно фиксировать переполнение.
Отметим, что в современных ЭВМ вся числовая информация со знаком записывается в дополнительном коде. Поэтому, например, число FFFFF...FFFF16 = -110.
Для быстрого перевода числа из прямого кода в дополнительный или наоборот, из дополнительного кода в прямой можно воспользоваться очень простым правилом.
Как уже указывалось, положительные числа в прямом и дополнительном кодах записываются одинаково. Так что здесь никаких проблем не возникает.
Для отрицательных чисел при переводе можно воспользоваться следующим правилом. Знак отрицательного числа, единица, естественно, сохраняется. А цифровые разряды меняются слева направо на противоположные до последней единицы в числе. Последняя единица и все следующие за ней разряды сохраняются:
0.10101100дк = 0.10101100пк; 0.00110011пк = 0.00110011дк.
1.10101100дк = 1.01010100пк; 1.00110011пк = 1.11001101дк.
Это правило вытекает из общего механизма перевода отрицательных чисел из прямого кода в дополнительный и наоборот. Первый шаг такого действия – инвертирование всех разрядов цифровой части (напомним, речь идет об отрицательных числах). При этом стоящие в конце числа нули станут единицами. На втором шаге к младшему разряду полученного результата добавляется единица. Это вызовет перенос, который будет распространяться до того разряда, который в новом числе равен нулю, а в исходном, следовательно, равен единице. Преобразование закончено.
Методы фиксации переполнения при алгебраическом суммировании чисел с фиксированной запятой в обратном и дополнительном кодах
Фиксация переполнения по знаку результата
Прежде всего, отметим, что переполнение разрядной сетки при суммировании чисел с фиксированной запятой возможно лишь для операндов, имеющих одинаковые знаки, так как, в противном случае, модуль результата окажется меньше модуля любого из операндов и, следовательно, переполнения не будет.
В связи с этим, факт наличия переполнения достаточно просто определить по изменению знака результата по сравнению со знаками операндов:
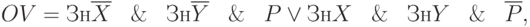
где P – перенос за пределы знакового разряда.