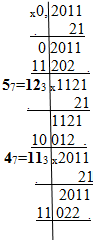Системы счисления. Перевод чисел из одной системы счисления в другую
Перевод чисел с фиксированной запятой (правильных дробей)
В этом случае исходное p-ичное число имеет следующий вид:
Ap = a-1*p-1+a-2*p-2+…+a-m*p-m
Основной метод, используемый для перевода чисел с фиксированной запятой из p ичной системы счисления в q-ичную заключается в следующем. В q-ичной системе счисления данная дробь будет иметь вид:
Bq = b-1*q-1+b-2*q-2+…+b-n*q-n...
Очевидно, что в новой системе счисления количество разрядов может отличаться от количества разрядов числа в исходной системе счисления и, более того, в новой системе счисления некоторые числа не могут быть представлены конечным числом знаков.
Погрешность числа в его новом представлении должна соответствовать его погрешности в исходной системе счисления, то есть
0,5 a-m*p-m= 0,5b-n*q-n
Отсюда, решая данное показательное уравнение относительно n, получаем
n = p lnn / lnq
На практике рекомендуется получить (n+1) знак в новом представлении дроби и округлить дробь до n знаков, используя общее правило округления: если (n+1)-я цифра больше или равна половине основания новой системы счисления, то к остающимся разрядам добавляется "1". В противном случае - "0".
Так, 0,543147 ≈ 0,54327.
А теперь рассмотрим собственно метод перевода. Для перевода правильной дроби из p-ичной системы счисления в q-ичную необходимой исходную дробь умножить на основание q новой системы счисления. Целая часть полученного результата даст старшую цифру дроби нового представления числа. Дробная часть результата будет использована на следующем шаге операции перевода. Операция проводится до получения необходимого количества знаков в новом представлении числа.
Этот метод достаточно легко обосновать.
Обоснование правила перевода правильных дробей
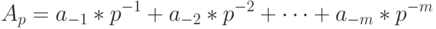 |
( 6.4) |
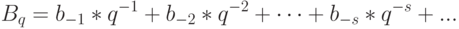 |
( 6.5) |
Ap*q = {D1,S1}, где D1 – целая часть результата, S1 – дробная часть результата.
Bq *q = {K1,R1}, где K1– целая часть результата, R1 – дробная часть результата.
Из (6.5): K1 = b-1.
Т.к. Ap≡ Bq, то b-1 = D1.
Умножив Bq на q, получим целую часть результата, равную b-1.
Так как Bq = Ap, то умножение AP на q в качестве целой части результата тоже даст b-1.
Аналогичные действия над полученной дробной частью результата позволят получать очередные цифры нового представления числа.
Пример 6.3. Перевести число с фиксированной запятой 0,652 из 10-й системы счисления в 4 ю.
Сначала определим необходимое количество знаков в новом числе: p=10, q=4, n=3.
m = 3 ln10/ln4 ≈ 5
Следовательно, в новом представлении числа нужно получить n+1 = 6 знаков и округлить число до 5 знаков.
Таким образом, 0,65210 = 0,2212324 ≈ 0,221304
Пример 6.4. Перевести число с фиксированной запятой 0,2011 из 3-й системы счисления в 7 ю.
Число знаков в новом представлении числа:
m = 4 ln7/ln3 ≈ 2
Учитываем, что 7 = 213.
Получаем: 0,20113 = 0,5457 ≈ 0,557