Рынок как система обслуживания случайных потоков
[+]
Опубликован: 26.10.2016 | Доступ: свободный | Студентов: 405 / 17 | Длительность: 08:16:00
Темы: Экономика, Менеджмент
Специальности: Менеджер, Экономист
Лекция 4:

Рынок как система с ожиданием
A
|
версия для печати
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

4.8. Пример. Расчет рынка нефти с сохранением непроданного товара

Проведем расчет рынка по тем же данным, которые мы задавали для рынка с явными потерями в "Рынок как система с явными потерями" (табл. 3.3). Поток предложения будем считать простейшим, система продажи полнодоступная, но в отличии от примера "Рынок как система с явными потерями" - система с ожиданием).

Для расчета потерь по второй формуле Эрланга можно использовать график, приведённый на рис. 4.3.

Поскольку мы имеем таблицы для числовой оценки Первой формулы Эрланга, мы используем следующие отношения для того, чтобы получить числовые значения 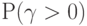Р (\gamma > 0), для второй формулы Эрланга [4],[8] .

\frac{1}{E_{2,\nu }}=\frac{1}{E_{1,\nu }}-\frac{1}{E_{1,\nu -1}} ( 4.16)

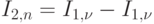I_{2,n}= I_{1,\nu}- I_{1,\nu} ( 4.17)

где I - инверсия вероятности

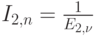
I_{2,n}=\frac{1}{E_{2,\nu }}

Известна также другая формула:

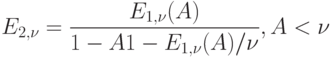E_{2,\nu }=\frac{E_{1,\nu }(A)}{1-A{1-E_{1, \nu }(A)/\nu }}, A< \nu ( 4.18)

где элемент 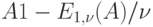A{1-E_{1, \nu }(A)/\nu } - средняя обслуженная нагрузка на канал в соответствующей системе с потерями. Для A\leq \nu мы имеем E_{2, \nu } (A) = 1. Это - вероятность того, что, и все клиенты поставлены на ожидание.

Мы будем использовать первую группу формул. Остальные показатели мы будем рассчитывать по формулам приведенным в табл. 4.1.

Данные расчетов приведены в табл. 4.2.

Таблица 4.2. Расчет потерь рынка нефти при системе с сохранением
Величина поставки (Ед. относ. потреб.) A Величина поставки (В млн. баррелей в день) Потери 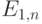E_{1,n} Потери 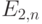E_{2,n} Потери 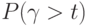P(\gamma > t) t > 1 Потери 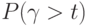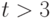P(\gamma > t) t > 3
1 2 3 4 5 6 7
1 2 7 0,000001
2 4 14 0, 000015 0
3 6 21 0, 000892 0.0015
4 8 28 0, 009931 0.0195 0.0072 0.0053
5 10 70 0, 03697 0.1056 0.0388 0.0053
6 12 42 0,085729 0.3191 0,0915 0,0159
7 14 49 0,144788 0.7792 0.2867 0.0388
8 16 56 0,212573
9 18 126 0,274114
10 20 140 0,329997

Рассмотрим результаты, полученные в табл. 4.2. Сравнивая данные столбцов 4 и 5.

Можно сделать вывод, что в системе с ожиданием вероятность передачи товара на хранение больше, чем величина потерь в системе с явными потерями. Например:

  • при поставке 12 относительных единиц (42 барреля в день )

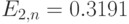    явные потери составляют E_{1,n} =0,085729, а вероятность передачи на хранение равна E_{2,n} =0.3191,

  • при поставке 14 относительных единиц (49 баррелей в день )

    явные потери составляют E_{1,n} =0,144788, а вероятность передачи на хранение равна E_{2,n}= 0.7792.

Хотя на практике передача товара на хранение не является потерей товаров, а потерей времени реализации. Реальные потери возникают только при условии долгого хранения. Тогда товар может просто испортиться и как при явных потерях снят с реализации, или затраты на хранение станут экономически не выгодными.

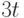В табл. 4.2 показаны вероятности задержки реализации на время t (столбец 6) и 3t (столбец 7). Расчет приведен для времени потребления 0,5 дня. Напомним, что относительное потребление рассчитано на поставку в течение дня, тогда 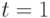t=1 день.

Тогда вероятность хранения больше одного дня больше вероятности явных потерь, но если время хранения равно 3 дням, то вероятность превышения сроков хранения меньше величины явных потерь.

Кроме того следует отметить, что система с потерями позволяет поставку большего количества товаров, чем система с ожиданием. В рассматриваемой таблице - это 16, 18 и 20 отн. единиц, хотя при больших потерях. Система с ожиданием позволяет реализовать без хранения величину поставки товаров, которая равна количеству потребителей.

Дальше >>
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

Вопросы и ответы

вопросов: 0