Рынок как система обслуживания случайных потоков
[+]
Опубликован: 26.10.2016 | Доступ: свободный | Студентов: 406 / 19 | Длительность: 08:16:00
Темы: Экономика, Менеджмент
Специальности: Менеджер, Экономист
Лекция 4:

Рынок как система с ожиданием
A
|
версия для печати
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

4.4. Среднее время ожидания для партий товаров, поступающих на рынок

Из теории вероятностей известно, что математическое ожидание

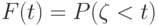непрерывной случайной величины \zeta с функцией распределения F (t)=P(\zeta < t) может быть определено из выражения

M= \intop\nolimits_{0}^{\infty }[1-F(t)]dt

Для рассматриваемой системы с ожиданием мы получим выражение

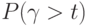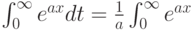
P(\gamma > t), так как 1-P(\gamma < t), то среднее время ожидания начала реализации (учитывая, что \intop\nolimits_{0}^{\infty }e^{ax}dt=\frac{1}{a}\intop\nolimits_{0}^{\infty }e^{ax}

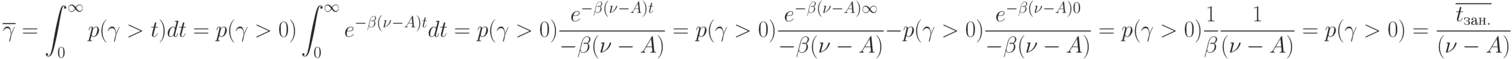\overline{ \gamma } =\intop\nolimits_{0}^{\infty } p(\gamma > t)dt= p(\gamma > 0) \intop\nolimits_{0}^{\infty }e^{-\beta (\nu -A)t}dt=p(\gamma > 0)\frac{e^{-\beta (\nu -A)t}}{-\beta (\nu -A)}=p(\gamma > 0)\frac{e^{-\beta (\nu - A)\infty}}{-\beta (\nu -A)}-p(\gamma > 0)\frac{e^{-\beta (\nu - A)0}}{-\beta (\nu -A)}=p(\gamma > 0)\frac{1}{\beta}\frac{1}{(\nu -A)}=p(\gamma > 0)=\frac{\overline {t_{зан.}}}{(\nu -A)} ( 4.12)

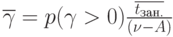Где \overline {t}_{зан.}=1/\beta - средняя длительность одного занятия одного потребителя \overline {\gamma}=p(\gamma > 0)\frac{\overline {t_{зан.}}}{(\nu -A)}- это среднее время ожидания по отношению ко всем поступившим партиям товаров (суммарное время ожидания, разделённое на все поступающие партии товаров).

4.5. Среднее время ожидания реализации для сохраняемых товаров

Все партии товаров, поступающие на рынок, можно разделить

на партии товаров, которые обслуживаются с сохранением (ожиданием реализации), и партии товаров, которые обслуживаются без сохранения

(ожидания реализации). Обозначим через \overline {\gamma_{зад}} - среднее время ожидания задержанных партий товаров. Время ожидания партий товаров, которые обслуживаются без сохранения (ожидания реализации) равно нулю. Тогда среднее время ожидания по отношению ко всем поступившим вызовам можно определить как среднее взвешенное:

\overline {\gamma}=\overline {\gamma}_{задер.}p(\gamma > 0)+0[1-p(\gamma > 0)]

Отсюда:

\overline {\gamma}=\overline {\gamma}_{задер.}p(\gamma > 0) ( 4.13)

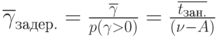\overline {\gamma}_{задер.} =\frac{\overline {\gamma}}{p(\gamma > 0)}=\frac{\overline {t_{зан.}}}{(\nu -A)} - суммарное время ожидания, разделённое на группы товаров, стоящие в очереди на реализацию.

Так как 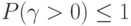P(\gamma > 0) \leq 1, то \overline {\gamma}_{задер.} \leq \overline {\gamma}.

Дальше >>
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

Вопросы и ответы

вопросов: 0