Рынок как система обслуживания случайных потоков
[+]
Опубликован: 26.10.2016 | Доступ: свободный | Студентов: 405 / 17 | Длительность: 08:16:00
Темы: Экономика, Менеджмент
Специальности: Менеджер, Экономист
Лекция 4:

Рынок как система с ожиданием
A
|
версия для печати
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

4.3. Вероятность того, что время хранения будет больше t

Вероятность Р(\gamma > 0) показывает того, что поступивший товар будет обслужен лишь после некоторого времени хранения (пребывания в очереди). Однако не дает ответа на весьма важный для обслуживания вопрос, как распределяется время хранения до начала потребления. В связи с этим определим функцию распределения времени начала обслуживания.

Исходные предположения рассматриваемой задачи:

  • показательное распределение длительности потребления
  • ожидающие реализации партии товаров обслуживаются в порядке поступления на хранение.

Обозначим через 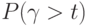P(\gamma > t) вероятность того, что партия товаров, поступившая в произвольный момент времени, попадет на хранение и время хранения будет больше t.

Через P_i (\gamma > t) обозначим указанную выше вероятность в предположении, что партия товаров поступит в момент времени, когда система находится в состоянии i, и через P_i вероятность того, что система находится в этом состоянии, т. е. в системе имеется точно i потребляемых и сохраняющихся партий товаров.

Имея в виду, что в рассматриваемой системе рынка поступившая партия товаров попадает на хранение лишь в случае, когда в момент её поступления в системе заняты все группы потребителей, на хранении находится 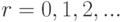r=0, 1, 2,... партий товаров, т. е. система находится в одном из состояний i=\nu, \nu +1, \nu +2, ..., по формуле полной вероятности получим

P(\gamma > t) = \sum_{i=0}^{\infty} P_i P_i (\gamma > t) ( 4.9)

Найдем вероятность p_i (\gamma > t) Если система находится в состоянии i(i \geq \nu), то непосредственно перед моментом поступления партии товаров в системе на ожидании реализации находится (i-\nu) партий товаров. Поступившая партия становится в очередь и на (i-\nu +1)-м месте. Поскольку партии товаров реализуются в порядке поступления ("первым пришел - первым обслуживается"), то, исходя из этого, вероятность того, что рассматриваемая партия товаров поступит на реализацию, равна вероятности того, что закончится потребление (i-\nu ) партий товаров.

Длительность потребления одной партии товара Т (без учета времени ожидания) распределена по показательному закону.

F(t)=p(T <t) =1- e^{-\beta t}

Функция распределения промежутков между моментами освобождения групп потребителей при условии занятости всех v потребителей есть.

F_{осв.} (t)= \pi_i (t) =1- e^{-\beta \nu t}

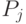Эта функция распределена по показательному закону, что определяет поток освобождений как простейший поток, параметр которого \lambda=\beta \nu. В соответствии с этим вероятность P_j того, что за время t окончится потребление точно j партий товаров, согласно формуле Пуассона, составляет

P_j=\frac{(\beta \nu t)^j}{j !}e^{-\beta \nu t}

а вероятность того, что за время t произойдет не более (i-\nu ) освобождений потребителей, если система находится в состоянии i,

p(\gamma > t)=\sum_{j=0}^{i-\nu }p_j=\sum_{j=0}^{i-\nu }\frac{(\beta \nu t)^j}{j !}e^{-\beta \nu t}

Далее

p(\gamma > t)=\sum_{j=0}^{\infty }p_i p_i(\gamma > t)= \sum_{j=0}^{\infty }p_i \sum_{j=0}^{i-\nu }\frac{(\beta \nu t)^j}{j !}e^{-\beta \nu t}

Подставим вместо P_i его значение из равенства (4.5 )

P_i=(\frac{A^V}{\nu !})(\frac{A}{\nu})^{i-\nu}P_0

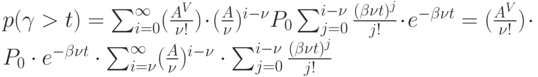
p(\gamma > t)=\sum_{i=0}^{\infty }(\frac{A^V}{\nu !})\cdot (\frac{A}{\nu })^{i-\nu }P_0 \sum_{j=0}^{i-\nu }\frac{(\beta \nu t)^j}{j !} \cdot e^{-\beta \nu t}=(\frac{A^V}{\nu !})\cdot P_0 \cdot e^{-\beta \nu t} \cdot \sum_{i=\nu }^{\infty }(\frac{A}{\nu})^{i-\nu } \cdot \sum_{j=0}^{i- \nu }\frac{(\beta \nu t)^j}{j!}

Изменим порядок суммирования. Учитывая, что:

\sum_{i=\nu }^{\infty } b^{i-\nu }\cdot \sum_{j=0}^{i-\nu }a^j=\sum_{i=0}^{i-\nu }a^j \cdot \sum_{i=\nu }^{\infty }b^{i-\nu }

\sum\nolimits_{i= \nu }^{ \infty } b^{i-\nu } \cdot \sum\nolimits_{j=0 }^{ i-\nu }a^j=b^0 \cdot a^0+b^1 \cdot (a^0 +a^1 ) +b^2 \cdot (a^0+ a^1+ a^2)+…+b^{\infty }\cdot (a^0+ a^1+…+a^{\infty })

\sum\nolimits_{j=0}^{i-\nu }a ^j \cdot \sum\nolimits_{i= \nu }^{ \infty }b^{i-\nu }=a^0 \cdot (b^0+b^1+…+b^{\infty})+a^{\infty }\cdot (b^{\infty})

Получим:

p(\gamma > t)=(\frac{A^V}{\nu !})\cdot P_0 \cdot e^{-\beta \nu t}\sum_{j=0}^{i-\nu }\frac{(\beta \nu t)^j}{j!}\cdot \sum_{i=\nu }^{\infty }(\frac{A}{\nu })^{i-\nu }=…

Каждое слагаемое последней суммы умножим и разделим на постоянную величину: (\frac{A}{\nu })^j

…=(\frac{A^V}{\nu !})\cdot P_0 \cdot e^{-\beta \nu t}\sum_{j=0}^{i-\nu }\frac{(\beta \nu t)^j}{j!}\cdot (\frac{A}{\nu })^j \cdot \sum_{i=\nu }^{\infty }(\frac{A}{\nu })^{i-(\nu +j)}

Обозначая i-(\nu +j)=x, получим:

\sum_{i=\nu }^{\infty}(\frac{A}{\nu })^{i-(\nu +j)}=\sum_{i=\nu }^{\infty }(\frac{A}{\nu })^x=\frac{1}{1-\frac{A}{\nu }}

Так как

P(\gamma > 0)= \sum\nolimits_{i=\nu }^{\infty }P_i=\frac{A^{\nu }}{\nu !}\cdot (\frac{A}{\nu !})^{i-\nu }\cdot P_0

и учитывая, что \beta = \frac{1}{t_{зан.}} и A=\lambda \cdot t_{зан.}, и обозначая r=i-\nu :

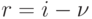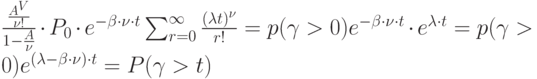
\frac{\frac{A^V}{\nu !}}{1-\frac{A}{\nu }}\cdot P_0 \cdot e^{-\beta \cdot \nu \cdot t}\sum_{r=0}^{\infty }\frac{(\lambda t)^{\nu }}{r!}=p(\gamma > 0)e^{-\beta \cdot \nu \cdot t}\cdot e^{\lambda \cdot t}= p(\gamma > 0)e^{(\lambda - \beta \cdot \nu)\cdot t}= P(\gamma > t)

Тогда вероятность того, что время хранения будет больше t равно:

p(\gamma >t)=p(\gamma >0)*e^((\lambda-\beta * \nu)*t) )

p(\gamma > t) =p(\gamma > 0)\cdot e^{(\lambda - \beta \cdot \nu)\cdot t}) ( 4.10)

Если за единицу измерения времени \gamma и t принять среднюю длительность потребления, то \beta =1 и p(\gamma > t)= p(\gamma > 0)e^{(\lambda -\nu )t}

Качество обслуживания поступающего потока вызовов в системах с ожиданием также характеризуют вероятности p_{задер.} (\gamma > t) того, что время ожидания начала реализации \gamma для партии товаров, попадающего на ожидание, будет больше t, т. е. для партий товаров, находящихся на хранении

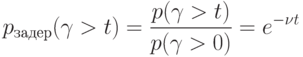p_{задер}(\gamma > t)=\frac{p(\gamma > t)}{p(\gamma > 0)}=e^{-\nu t} ( 4.11)

Дальше >>
< Лекция 3 || Лекция 4: 123456 || Лекция 5 >

Вопросы и ответы

вопросов: 0