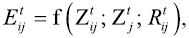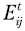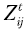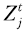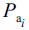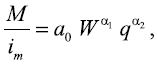|
Чтоб сдать данный тест, пришлось рыскать по всему учебнику, вплоть до 33-ей лекции. Хотелось бы, чтобы при прохождении теста проверялось то, что было изучено непосредственно в теме.. |
Опубликован: 03.08.2016 | Доступ: свободный | Студентов: 1322 / 203 | Длительность: 44:47:00
Темы: Экономика, Менеджмент
Специальности: Менеджер, Руководитель, Экономист
Лекция 8:
Экономико-математическое моделирование мирохозяйственных связей
8.2. Гравитационные модели
Для моделирования товарных потоков между парами стран построены специальные эконометрические модели, получившие название гравитационных. Каждая модель представляет собой функцию, связывающую товарный поток с несколькими факторами: социально-политическими, экономическими, географическими. Гравитационные модели определяют зависимость однонаправленного внешнеторгового потока от параметров внутриэкономического состояния как страны-экспортера, так и страны-импортера.
В основе названия гравитационных моделей лежит известная из физики формула притяжения. Впервые в экономических процессах эта формула была применена для описания зависимости между продавцом в городе и покупателем, живущим за городом, исходя из предпосылки, что их "притягивает" друг к другу:
| где | Mij | - | показатель "притягивания" (например, число поездок); |
| Pi | - | численность населения в городе; | |
| dij | - | расстояние от клиента до центра; | |
| k | - | некоторый коэффициент. |
В общем случае гравитационная модель экспорта представляет собой экономическую функцию, связывающую товарный поток из страны или региона i в страну или регион j с различными факторами, в том числе с издержками по продвижению потока из i в j:
| где | - | экспорт из страны (региона) i в страну (регион) j; | |
| - | внутренние факторы страны i, определяющие экспортноепредложение; | ||
| - | внутренние факторы страны j, определяющие импортный спрос; | ||
| - | фактор интенсивности товарного потока из i в j, определяемыйгеографическим положением торгующих стран и особенностямитранспортировки (вид транспорта, расстояние и т.п.). |
Одна из первых моделей экспорта была предложена известным голландским экономистом Я. Тинбергеном. Зависимость интенсивности товарного потока от расстояния между торгующими странами и обусловленность импорта страны величинами их валового национального продукта (ВНП) задается формулой
| где | Eij | - | экспорт из страны i в страну j; |
| a0 | - | константа; | |
| Yi | - | ВНП страны i; | |
| Yj | - | ВНП страны j; | |
| Dij | - | расстояние между странами i и j; | |
| α1 | - | коэффициент эластичности экспорта от ВНП страны-экспортера; | |
| α2 | - | коэффициент эластичности экспорта от ВНП страны-импортера; | |
| α3 | - | коэффициент эластичности экспорта от расстояния между i и j. |
Другая модель экспорта выражает зависимость величины межстранового товарного потока от национального дохода стран-экспортеров и стран-импортеров, расстояния между ними, величины транспортных тарифов и др.:
| где | Ecij | - | экспорт из i в j; |
| a | - | константа; | |
| Ci | - | параметр экспорта i; | |
| Cj | - | параметр импорта j; | |
| Ni, Nj | - | национальный доход соответственно стран i и j; | |
| Dij | - | расстояние между странами i и j; | |
| α | - | параметр эластичности экспорта от дохода; | |
| β | - | параметр эластичности импорта от дохода; | |
| γ | - | коэффициент транспортных расходов на одну морскую милю; | |
| δ | - | "параметр изоляции". |
Примером модели импорта может служить модель, разработанная для национальной экономики США:
| где | Mi | - | импорт товара i; |
| Xi | - | емкость внутреннего рынка по этому товару; | |
| - | импортная цена; | ||
| - | цена внутреннего потребления; | ||
| Ti | - | импортная пошлина; | |
| Vi | - | ошибка расчетов; | |
| β1, β2, β3 | - | соответствующие коэффициенты эластичности. |
Еще одна модель импорта была разработана для известного проекта международной торговли ЛИНК (о нем см. ниже):
| где | M | - | объем валового импорта в текущих ценах; |
| im | - | индекс импортных цен; | |
| q | - | отношение индексов цен внутреннего рынка к отношению индексов импортных цен; | |
| α1 и α2 | - | соответствующие коэффициенты эластичности; | |
| W | - | показатель "экономической активности": |
Гравитационные модели международной торговли продолжают свое развитие и в настоящее время. В своем исследовании, посвященном роли ВТО в международной торговле, профессор школы бизнеса Калифорнийского университета Э. Роуз использовал стандартную гравитационную модель двусторонней торговли. На основе статистических данных за период 1948-1999 гг. для 178 стран он приходит к выводу, что эффект от членства в ГАТТ - ВТО экономически несуществен, часто негативен и находится в пределах статистической ошибки. Используя более 60 индикаторов степени либерализации торговой политики (например, соотношение объема импорта к ВВП, уровни тарифной и нетарифной защиты), Роуз исследует данные о торговле 168 стран за период с 1950 по 1998 г. и не находит существенной зависимости между степенью свободы торговой политики и членством в ВТО.
Андрей Кудырский