Методы дедуктивных и индуктивных рассуждений
Нечёткие рассуждения и выводы
Нежная Правда в красивых одеждах ходила,
Принарядившись для сирых, блаженных, калек, -
Грубая Ложь эту Правду к себе заманила:
Мол, оставайся-ка ты у меня на ночлег.
В. Высоцкий. Притча о Правде и Лжи
В теории предикатов отмечалось наличие кванторов общности и существования, как действенных операторов чёткого, точного единственного логического вывода. Эти кванторы являются основой стройной и полной формулировки, а также точного доказательства математических теорем.
Кванторы общности и существования следует считать классическими.
Однако для неточных, приближённых, даже эмоциональных оценок широко используются так называемые квантификаторы, которыми так красочно снабжена речь человека, и которые не только участвуют в рассуждениях, но и формируют выводы.
Конечно, эти выводы не следует считать строгими. Чаще всего они отражают индивидуальное восприятие писателя, поэта, художника-формалиста.
К сожалению, часто квантификаторы используются в софистических спорах с оппонентами в интересах политики, экономики, социологии и др.
Для формализации мышления рассматриваются нечёткие квантификаторы, связанные с нечёткой математикой, основанной Л. Заде.
Основным объектом изучения нечёткой математики являются нечёткие множества на основе определения:
Элемент а принадлежит данному нечёткому множеству А со степенью уверенности 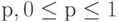 .
.
Мнения относительно принадлежности элемента нечёткому множеству никогда не бывает однозначным. Отсюда – заведомо неточные выводы. Именно поэтому разрабатываются ГОСТы – государственные стандарты.
В Лекции 1 для перехода к логическим нейронным сетям указанная выше степень уверенности в истинности высказываний была определена как достоверность высказывания (о принадлежности данных). Достоверность – это вероятность того, что данное высказывание истинно, зачастую взятая "с потолка".
Доказывая "полезность" и эффективность применения логических нейронных сетей, лектору приходится убеждать слушателей в том, что жизнь полна неопределённости и противоречий, что сказывается на процессе возбуждения рецепторов. Но мы живём! Ибо человек – общественное животное. Коллектив (народ) поправит.
Введём понятие лингвистической шкалы, как последовательности нечётких квантификаторов, относящихся к оценке элементов нечёткого множества по одному и тому же основанию (расстоянию, длительности, частоте, размерам и т.п.)
Примером лингвистической шкалы может служить шкала расстояний: вплотную, очень близко, близко, ни далеко ни близко, далеко, очень далеко, в бесконечности.
Другой пример – шкала размеров: крошечный, очень маленький, маленький, средний, большой, очень большой, огромный.
Для лингвистических шкал возможно принятие решений ("гостирование") о численных оценках и их границах в метрах, часах, квадратных километрах и т.п. Интервалы оценок и нечёткие квантификаторы образуют взаимно-однозначное соответствие. Именно такой подход реализуется во многих системах принятия решений на логических нейронных сетях – при формировании рецепторного слоя.
Перейдём к нечётким рассуждениям.
Один шаг достоверного (дедуктивного) вывода можно представить в виде схемы:
 |
( 4.5) |
Например, запишем одиннадцатую аксиому исчисления высказываний:
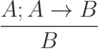 |
( 4.6) |
Введём некоторые нечёткие квантификаторы и изменим схему (4.6):
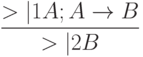
Здесь >|1 – нечёткий квантификатор, показывающий, что истинность А не является абсолютной. Поскольку в этом случае вывод не может быть достоверным, для степени его достоверности необходимо ввести некоторый квантификатор >|2.
Конкретизируем пример:
Часто идёт дождь; Когда идёт дождь, я не выхожу на улицу
-------------------------------------------------------.
? Я не выхожу на улицу
Здесь часто - квантификатор >|1. Знак вопрос стоит вместо квантификатора >|2, который по интуиции логично принять за тот же >|1 "часто". Вывод "часто я не выхожу на улицу" выглядит вполне логичным.
Рассмотрим другую схему:
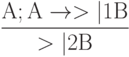
Развивая предыдущий пример, запишем:
Идёт дождь; Когда идёт дождь, я редко хожу гулять
-------------------------------------------------.
? Я редко хожу гулять
Какой квантификатор здесь надо поставить? Однозначный ответ вряд ли возможен, ведь отсутствует информация о частоте события А.
Рассмотрим, наконец, схему
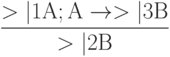
, при конкретной реализации:
Часто идёт дождь; Когда идёт дождь, я редко хожу гулять
-------------------------------------------------------.
? Я хожу гулять
Здесь выбор квантификатора более обоснован. Однако если использовать часто, то возникает некоторая синхронность гуляния с частотой дождя. Но ведь во время дождя "гуляние" происходит редко. Остаётся использовать "иногда", как бы суммируя как отсутствие дождя, так и прогулки под дождём.
Численные оценки квантификаторов неотделимы от "физического смысла": "дача далеко от Москвы" предполагает другую оценку расстояния, чем "Петербург далеко от Москвы".
Принцип ситуационной инвариантности позволяет, проводя рассуждения для одной ситуации, преобразовать его формальным образом для сходных ситуаций.
Для этого используется лингвистическая шкала. Переход от ситуации к ситуации связан со смещением всех интервалов, соответствующих квантификаторам шкалы, на определённое число позиций влево или вправо по множеству значений признака, учитываемого данной лингвистической шкалой. Такое смещение позволяет использовать в нечётких рассуждениях элементы рассуждений по аксиомам, так как в основе этих рассуждений лежит идея сходства, похожести.
В дополнение рассмотренных схем, в [Посп] приводится ряд схем правдоподобных рассуждений: вероятностные схемы рассуждений, схемы с учётом необходимых условий и др.
Краткие итоги
- Деревья вывода (деревья логических возможностей), как и логические сети, предоставляют возможности автоматизации дедуктивного(правдоподобного) вывода, если совместить логику со смысловым наполнением вершин в рамках одного языка.
- Возможен переход к рассмотрению вероятностных деревьев и логических сетей, что погружает проблему автоматизации в область действия математической логики событий.
- Правдоподобные (индуктивные) рассуждения приводят к выработке лишь гипотезы, которая подвергается проверкой фактами..
- Принципы причинно-следственных отношений Д.С. Милля позволили сформулировать метод индуктивного мышления.
- Нечёткие рассуждения и выводы формируются с помощью квантификаторов и лингвистических шкал.
Вопросы
- Приведите пример вывода по дереву логических возможностей.
- Представьте схему доказательства истинности индуктивных рассуждений.
- Обсудите проблему эмпирической и теоретической истины.
- Каковы принципы причинно-следственных отношений Д.С. Милля?
- Поясните ход рассуждений по методу индуктивного мышления Д.С. Милля.
- Охарактеризуйте нечёткие рассуждения и выводы.
