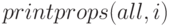Задачи высшей математики с Maxima
3.8.4 Операторный метод решения
Для решения систем обыкновенных линейных дифференциальных уравнений в Maxima имеется функция 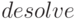 . Работа функции
. Работа функции 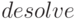 основана на преобразовании Лапласа заданных дифференциальных уравнений.
основана на преобразовании Лапласа заданных дифференциальных уравнений.
Пусть задана функция действительного переменного  , которая удовлетворяет следующим условиям:
, которая удовлетворяет следующим условиям:
- однозначна и непрерывна вместе со своими производными
 -го порядка для всех
-го порядка для всех 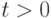 , кроме тех, где она и ее производные имеют разрывы 1-го рода. При этом в каждом конечном интервале изменения имеется конечное число точек разрыва;
, кроме тех, где она и ее производные имеют разрывы 1-го рода. При этом в каждом конечном интервале изменения имеется конечное число точек разрыва; -
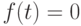 для всех
для всех 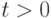 ;
; - возрастает медленнее некоторой экспоненциальной функции
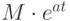 , где
, где  и
и  — некоторые положительные величины, т.е. всегда можно указать такие
— некоторые положительные величины, т.е. всегда можно указать такие  и
и  , чтобы при любом
, чтобы при любом 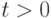 соблюдалось неравенство
соблюдалось неравенство 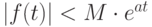 .
.
Рассматриваемой функции  ставится в соответствие новая функция, определяемая равенством
ставится в соответствие новая функция, определяемая равенством
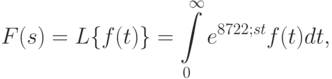
 — положительное действительное число или комплексное число с положительной действительной частью.
— положительное действительное число или комплексное число с положительной действительной частью.Функция  при этом называется оригиналом, а
при этом называется оригиналом, а 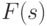 — изображением функции
— изображением функции  по Лапласу. Переход от оригинала к изображению называется преобразованием Лапласа. Соответственно, обратный переход от изображения к оригиналу называется обратным преобразованием Лапласа.
по Лапласу. Переход от оригинала к изображению называется преобразованием Лапласа. Соответственно, обратный переход от изображения к оригиналу называется обратным преобразованием Лапласа.
Для преобразования Лапласа выполняется теорема единственности: если две непрерывные функции  и
и  имеют одно и то же изображение по Лапласу
имеют одно и то же изображение по Лапласу 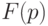 , то они тождественно равны.
, то они тождественно равны.
С помощью операционного исчисления можно сравнительно просто решать различные задачи, сводящиеся к интегрированию линейных дифференциальных уравнений. Переход от исходных функций к их изображениям позволяет заменить решение системы дифференциальных уравнений решением системы алгебраических уравнений (но при этом обратное преобразование Лапласа может быть достаточно сложной задачей).
При вычислении преобразования Лапласа производные заменяются алгебраическими выражениями следующего вида:
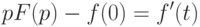

Использование 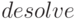 ограничивается одним из свойств преобразования Лапласа: если
ограничивается одним из свойств преобразования Лапласа: если  , то
, то  . Поэтому
. Поэтому 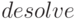 предполагает, что решается система ОДУ с постоянными коэффициентами.
предполагает, что решается система ОДУ с постоянными коэффициентами.
Синтаксис вызова  , где
, где 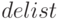 — список решаемых дифференциальных уравнений,
— список решаемых дифференциальных уравнений, 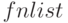 — список искомых функций. При использовании
— список искомых функций. При использовании 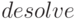 необходимо явно задавать функциональные зависимости (вместо
необходимо явно задавать функциональные зависимости (вместо 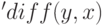 использовать запись
использовать запись 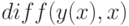 ).
).
Примеры использования 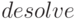 :
:
Система ОДУ первого порядка:
(%i1) de1:diff(f(x),x)=diff(g(x),x)+sin(x);
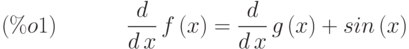
(%i2) de2:diff(g(x),x,2)=diff(f(x),x) - cos(x);
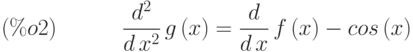
(%i3) desolve([de1,de2],[f(x),g(x)]);

![g\left( x\right) ={e}^{x}\left( \left. \frac{d}{dx}g\left( x\right) \right|_{x=0}\right) -\left. \frac{d}{dx}g\left( x\right) \right|_{x=0}+cos\left( x\right) +g\left( 0\right) -1]](/sites/default/files/tex_cache/fc6fd206c7a47c96937e8bba61e3ecd6.png)
Единичное дифференциальное уравнение второго порядка:
(%i1) de3:diff(f(x),x,2)+f(x) = 2*x;
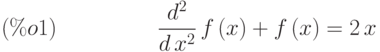
(%i2) desolve(de3,f(x));
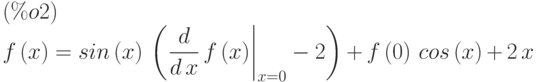
Для указания начальных условий используется функция  .
.
Синтаксис вызова: a![tvalue(expr, [x_1 = a_1,...,x_m = a_m],c) atvalue(expr,x_1 = a_1,c)](/sites/default/files/tex_cache/99a97c9f899b35303ecf248b06f889fe.png)
Функция  присваивает значение c выражению
присваивает значение c выражению  в точке
в точке 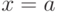 . Выражение
. Выражение  — функция
— функция 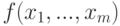 или производной
или производной 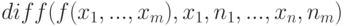 Здесь
Здесь 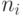 — порядок дифференцирования по переменной
— порядок дифференцирования по переменной  .
.
Пример использования 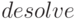 и
и  :
:
(%i1) de1:diff(f(x),x)=diff(g(x),x)+sin(x);
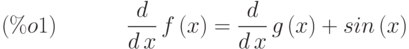
(%i2) de2:diff(g(x),x,2)=diff(f(x),x) - cos(x);
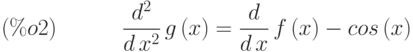
(%i3) atvalue(f(x),x=0,1);

(%i4) atvalue(g(x),x=0,2);

(%i5) atvalue(diff(g(x),x),x=0,3);

(%i6) desolve([de1,de2],[f(x),g(x)]);
![[f\left( x\right) =3\,{e}^{x}-2,g\left( x\right) =cos\left( x\right) +3\,{e}^{x}-2]\leqno{(\%o6) }](/sites/default/files/tex_cache/7051bec280590f3f9112c509bdf68e2d.png)
Управление начальными условиями осуществляется при помощи функций  и
и 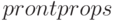 . Функция
. Функция  (синтаксис вызова —
(синтаксис вызова —  ) печатает свойства переменной (атома
) печатает свойства переменной (атома  ), а функция
), а функция 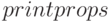 печатает информацию о заданном свойстве переменной. Кроме того, функция
печатает информацию о заданном свойстве переменной. Кроме того, функция  вычисляет значение выражения в заданной точке с учетом свойства
вычисляет значение выражения в заданной точке с учетом свойства  .
.
Синтаксис вызова 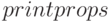 :
:
Данная функция позволяет просмотреть свойства атома  (или группы атомов Lisp, указанных в списке), определённые индикатором
(или группы атомов Lisp, указанных в списке), определённые индикатором  .
.
Отмена установок, произведённых  , осуществляется функцией
, осуществляется функцией 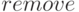 (удаление свойства
(удаление свойства  у атомов
у атомов  осуществляется вызовом remove(a1,p1,... ,an,pn); удаление списка свойств — вызовом
осуществляется вызовом remove(a1,p1,... ,an,pn); удаление списка свойств — вызовом ![remove([a_1,... ,a_m], [p_1,... ,p_n],...)](/sites/default/files/tex_cache/460f191644caeb9663ecbf7c932c6eda.png) ).
).
Пример синтаксиса и использования рассмотренных функций:
(%i1) eq1:'diff(f(x),x)='diff(g(x),x)+sin(x);
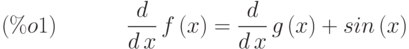
(%i2) eq2:'diff(g(x),x,2)='diff(f(x),x)-cos(x);
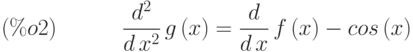
(%i3) atvalue('diff(g(x),x),x=0,a);
(%i4) atvalue(f(x),x=0,1);

(%i5) properties(f);
![[atvalue]\leqno{(\%o5) }](/sites/default/files/tex_cache/db6805ad13f62bf540e346f1b6854697.png)
(%i6) printprops(f,atvalue);


(%i7) desolve([eq1,eq2],[f(x),g(x)]);
![[f\left( x\right) =a\,{e}^{x}-a+1,g\left( x\right) =cos\left( x\right) +a\,{e}^{x}-a+g\left( 0\right) -1]\leqno{(\%o7) }](/sites/default/files/tex_cache/698e94f90e28e91ba5ed175218a02a11.png)
(%i8) at(%,[x=1]);
![[f\left( 1\right) =e\,a-a+1,g\left( 1\right) =e\,a-a+cos\left( 1\right) +g\left( 0\right) -1]\leqno{(\%o8) }](/sites/default/files/tex_cache/446635b652a92e29ed0985f563a23cdb.png)
Ещё один пример анализа свойств:
(%i9) atvalue (f(x,y), [x = 0, y = 1], a^2);

(%i10) atvalue ('diff (f(x,y), x), x = 0, 1 + y);
(%i11) printprops (all, atvalue);
![\left. \frac{d}{d\,@1}\,g\left( @1\right) \right|_{[@1=0]}=a\\
\left. \frac{d}{d\,@1}\,f\left( @1,@2\right) \right|_{[@1=0]}=@2+1\\
f\left( 0,1\right) ={a}^{2}\\
f\left( 0\right) =1](/sites/default/files/tex_cache/cd1d732ba195188cdfb7d8035b74767a.png)



![printprops([a1,... ,an],i)](/sites/default/files/tex_cache/40c282d250d440957badc9b0b91012dc.png)