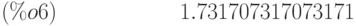Задачи высшей математики с Maxima
3.6.2 Приближённое вычисление определённых интегралов
Степенные ряды эффективны и удобны при приближённом вычислении определённых интегралов, не выражающихся в конечном виде через элементарные функции. Для вычисления  подинтегральная функция
подинтегральная функция  раскладывается в степенной ряд. Если
раскладывается в степенной ряд. Если
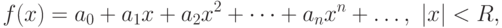
 степенной ряд можно интегрировать почленно. Получаем метод вычисления интеграла
степенной ряд можно интегрировать почленно. Получаем метод вычисления интеграла  с любой наперёд заданной
точностью
с любой наперёд заданной
точностью
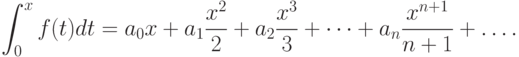
Пример: Приближённое вычисление интеграла вероятностей
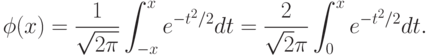
Так как
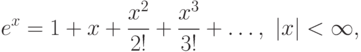

Подставив этот ряд под знак интеграла и произведя почленное интегрирование получаем
![\phi(x)=\frac{2}{\sqrt{2\pi}}\int_{0}^{x}e^{-t^{2}/2}dt=
\frac{2}{\sqrt{2\pi}}\left[x-\frac{x^{3}}{3\cdot 2}+\frac{x^{5}}
{5\cdot 2^{2}\cdot 2!}-\frac{x^{7}}{7\cdot 2^{3}\cdot 3!}+\dots\right]](/sites/default/files/tex_cache/e86d7753cd0478863c9d6b87d6ac3779.png)
Так как это знакопеременный ряд с последовательно убывающими слагаемыми, то погрешность вычисления интеграла последовательно убывает и не превышает последнего слагаемого.
Рассмотрим пример приближённого представления интеграла в виде полинома некоторой степени в том случае, когда он не вычисляется в замкнутой аналитической форме.
Пример: Вычислить 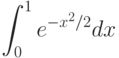 , оценить достигнутую точность
, оценить достигнутую точность
Используем разложение подинтегральной функции в ряд. Подставляя в полученное выражение  , вычисляем искомый интеграл. Так как исследуемый ряд знакопеременный, погрешность замены бесконечной суммы конечным выражением по абсолютной величине не превышает первого отброшенного члена.
, вычисляем искомый интеграл. Так как исследуемый ряд знакопеременный, погрешность замены бесконечной суммы конечным выражением по абсолютной величине не превышает первого отброшенного члена.
(%i1) f(x):=exp(-x^2/2);

(%i2) taylor(f(x),x,0,8);
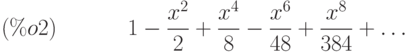
Интегрируя в пределах от 0 до 1, получаем числовой результат:
(%i3) integrate(%,x,0,1);

(%i4) float(%);

Точность расчёта оцениваем, интегрируя в пределах от 0 до  :
:
(%i5) integrate(%o2,x,0,a);
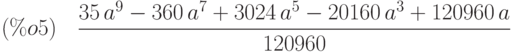
При 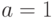 находим:
находим:
(%i6) expand(%);
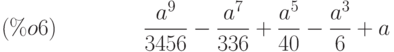
(%i7) float(1/3456);
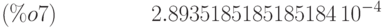
Таким образом, точность расчёта значения интеграла  , не хуже 0,0003. Окончательно
, не хуже 0,0003. Окончательно
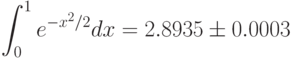
3.7 Преобразование степенных рядов
Пакет Maxima позволяет не только строить разложение различных функций в степенные ряды, но и представления их в виде дробнорациональной функции (аппроксимация Паде) или цепной дроби.
Аппроксимацией Паде для функции  , заданной степенным рядом, называется такая дробно-рациональная функция
, заданной степенным рядом, называется такая дробно-рациональная функция  , чьё разложение в степенной ряд совпадает со степенным рядом
, чьё разложение в степенной ряд совпадает со степенным рядом  с точностью до коэффициента при
с точностью до коэффициента при 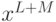 .
.
Паде-аппроксиммант задаётся значением функции в заданной точке и 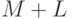 значениями её производных в этой же точке. Эта же информация может послужить основой для степенного ряда, так в чём же отличие? Главное отличие в том, что задав
значениями её производных в этой же точке. Эта же информация может послужить основой для степенного ряда, так в чём же отличие? Главное отличие в том, что задав 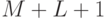 член степенного ряда, мы отбрасываем остальные члены ряда, приравнивая их к нулю. Паде-аппроксимант не является полиномом, поэтому задав
член степенного ряда, мы отбрасываем остальные члены ряда, приравнивая их к нулю. Паде-аппроксимант не является полиномом, поэтому задав 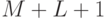 членов разложения Паде-аппроксиманта в степенной ряд, мы в неявной форме задаём и остальные члены.
членов разложения Паде-аппроксиманта в степенной ряд, мы в неявной форме задаём и остальные члены.
Чему эти дополнительные члены будут равны? Это вопрос, на который нет однозначного ответа. В одних случаях они позволят нам построить более точную аппроксимацию, в других — наоборот могут ухудшить положение. Нет способа, который позволил бы сказать, насколько точна окажется Паде-аппроксимация и в какой окрестности и с какой точностью можно получить результаты.
Ещё одним недостатком этого метода является то, что он требует информации не о значениях функции, а о её производных высших порядков, которые могут быть значительно большими по абсолютной величине, чем сами значения функции.
Паде-аппрокимация наиболее эффективна для функций, имеющих полюса на комплексной плоскости в окрестностях точки разложения. Например, функция 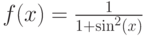 непрерывна на действительной оси, но имеет полюса на комплексной плоскости. Поэтому она неэффективно аппроксимируется степенным рядом (до шестой степени включительно), но хорошо аппроксимируется по Паде со степенями числителя и знаменателя равными 4 и 2.
непрерывна на действительной оси, но имеет полюса на комплексной плоскости. Поэтому она неэффективно аппроксимируется степенным рядом (до шестой степени включительно), но хорошо аппроксимируется по Паде со степенями числителя и знаменателя равными 4 и 2.
Функция  , представленная в пакете Maxima, аппроксимирует отрезок ряда Тейлора, содержащий слагаемые до
, представленная в пакете Maxima, аппроксимирует отрезок ряда Тейлора, содержащий слагаемые до  -го порядка включительно, дробно-рациональной функцией. Её аргументы — ряд Тейлора, порядок числителя n, порядок знаменателя
-го порядка включительно, дробно-рациональной функцией. Её аргументы — ряд Тейлора, порядок числителя n, порядок знаменателя  . Разумеется, количество известных коэффициентов ряда Тейлора должно совпадать с общим количеством коэффициентов в дробно-рациональной функции минус один, поскольку числитель и знаменатель определены с точностью до общего множителя.
. Разумеется, количество известных коэффициентов ряда Тейлора должно совпадать с общим количеством коэффициентов в дробно-рациональной функции минус один, поскольку числитель и знаменатель определены с точностью до общего множителя.
Синтаксис вызова функции  :
:
pade (ряд Тейлора, степень числителя, степень знаменателя)
Вместо ряда Тейлора может использоваться ряд Лорана. В этом случае степени числителя и знаменателя могут быть и бесконечными (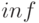 ). В этом случае рассматриваются все рациональные функции, суммарная степень которых меньше или равна длине степенного ряда.
). В этом случае рассматриваются все рациональные функции, суммарная степень которых меньше или равна длине степенного ряда.
Пример:
(%i1) t:taylor(exp(x),x,0,3);
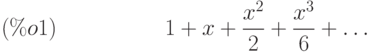
(%i2) pade(t,1,2);
![[\frac{2\,x+6}{{x}^{2}-4\,x+6}]\leqno{(\%o2) }](/sites/default/files/tex_cache/4954312eb90dcfedc85101e21190b059.png)
(%i3) taylor(sin(x)/x,x,0,7);

(%i4) pade(%,2,4);
![[-\frac{620\,{x}^{2}-5880}{11\,{x}^{4}+360\,{x}^{2}+5880}]\leqno{(\%o4) }](/sites/default/files/tex_cache/4e50a26200c5d57312e69e59449a9a55.png)
(%i5) taylor (1/(cos(x) - sec(x))^3, x, 0, 5);
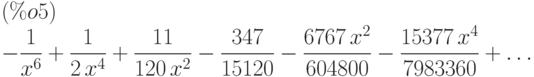
(%i6) pade(%,3,inf);
![[-\frac{120}{41\,{x}^{10}+60\,{x}^{8}+120\,{x}^{6}},\frac{8806092\,{x}^{2}-16847160}{1353067\,{x}^{10}-382512\,{x}^{8}+16847160\,{x}^{6}}]\leqno{(\%o6) }](/sites/default/files/tex_cache/27f325ebcfe303b34a82110a3cff6d22.png)
Более специфичной является функция 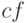 , которая рассчитывает коэффициенты цепной дроби, аппроксимирующей заданное выражение. Синтаксис вызова —
, которая рассчитывает коэффициенты цепной дроби, аппроксимирующей заданное выражение. Синтаксис вызова — 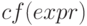 . Выражение
. Выражение  должно состоять из целых чисел, квадратных корней целых чисел и знаков арифметических операций. Функция возвращает список коэффициентов (непрерывная дробь
должно состоять из целых чисел, квадратных корней целых чисел и знаков арифметических операций. Функция возвращает список коэффициентов (непрерывная дробь 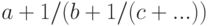 представляется списком [
представляется списком [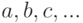 ]). Флаг
]). Флаг  определяет количество периодов цепной дроби. Изначально установлено значение 1. Функция
определяет количество периодов цепной дроби. Изначально установлено значение 1. Функция  преобразует список (как правило выдачу функции
преобразует список (как правило выдачу функции 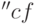 ) в собственно цепную дробь вида
) в собственно цепную дробь вида 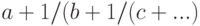 ).
).
Примеры использования функций 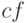 и
и  :
:
(%i1) cf ([1, 2, -3] + [1, -2, 1]);
![[1,1,1,2]\leqno{(\%o1) }](/sites/default/files/tex_cache/118db328675d3ebbd1bf7e38414c7177.png)
(%i2) cfdisrep (%);

(%i3) cflength: 3;

(%i4) cf (sqrt (3));
![[1,1,2,1,2,1,2]\leqno{(\%o4) }](/sites/default/files/tex_cache/701789772e01f88a90cbe9ac8ad9d552.png)
(%i5) cfdisrep(%);
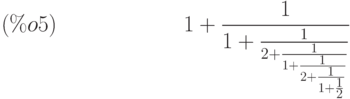
(%i6) ev (%, numer);