|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Компания ALT Linux
Опубликован: 07.03.2015 | Доступ: свободный | Студентов: 2214 / 538 | Длительность: 24:14:00
Тема: Программирование
Специальности: Программист, Архитектор программного обеспечения
Лекция 3:
Операторы управления
Задача 3.7. Заданы коэффициенты  и
и  биквадратного уравнения
биквадратного уравнения 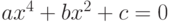 . Найти все его действительные корни.
. Найти все его действительные корни.
Входные данные: 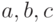 .
.
Выходные данные: 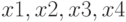 .
.
Для решения биквадратного уравнения необходимо заменой 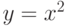 привести его к квадратному уравнению
привести его к квадратному уравнению 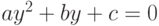 и решить это уравнение.
и решить это уравнение.
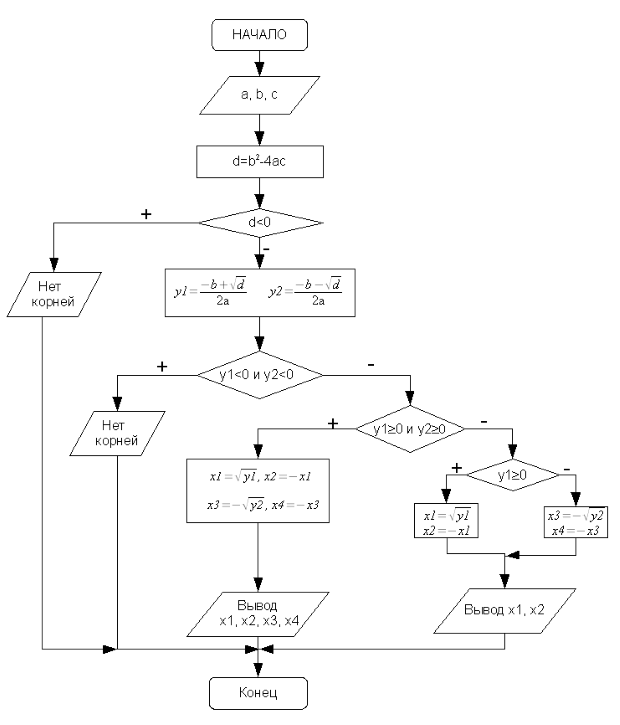
Опишем алгоритм решения этой задачи (рис. 3.18):
- Ввод коэффициентов биквадратного уравнения
 и
и  (блок 1).
(блок 1). - Вычисление дискриминанта уравнения
 (блок 2).
(блок 2). - Если d < 0 (блок 3), вывод сообщения, что корней нет (блок 4), а иначе определяются корни соответствующего квадратного уравнения y1 и y2(блок 5).
- Если y1 < 0 и y2 < 0 (блок 6), то вывод сообщения, что корней нет (блок 7).
- Если y1 >= 0 и y2 >= 0 (блок 8), то вычисляются четыре корня по формулам
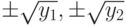 (блок 9) и выводятся значения корней (блок 10).
(блок 9) и выводятся значения корней (блок 10). - Если условия 4) и 5) не выполняются, то необходимо проверить знак y1. Если y1 >= 0 (блок 11), то вычисляются два корня по формуле
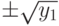 (блок 12), иначе (если y2 >= 0) вычисляются два корня по формуле
(блок 12), иначе (если y2 >= 0) вычисляются два корня по формуле  (блок 13). Вывод вычисленных значений корней (блок 14).
(блок 13). Вывод вычисленных значений корней (блок 14).
Текст программы решения биквадратного уравнения приведён ниже.
Внимание! Если в условном операторе проверяется двойное условие, необходимо применять логические операции ||, &&, !.Например, условие "если y1 и y2 положительны" правильно записать так: if (y1>=0 && y2>=0).
#include <iostream>
#include <math.h>
using namespace std;
int main ( )
{ //Описание переменных:
//a, b, c - коэффициенты биквадратного уравнения,
//d - дискриминант,
// x1, x2, x3, x4 - корни биквадратного уравнения,
//y1, y2 - корни квадратного уравнения ay^2+by+c =0,
float a, b, c, d, x1, x2, x3, x4, y1, y2;
//Ввод коэффициентов уравнения.
cout<<" a = "; cin >>a;
cout<<" b = "; cin >>b;
cout<<" c = "; cin >>c;
d=b* b-4*a*c; //Вычисление дискриминанта.
if ( d<0) //Если дискриминант отрицательный, вывод сообщения "Корней нет".
cout<<" Нет действительных корней \ n ";
else //Если дискриминант положительный,
{
//Вычисление корней соответствующего квадратного уравнения .
y1=( -b+sqrt ( d ) ) /2/ a;
y2=( -b- sqrt ( d ) ) /(2 * a );
//Если оба корня квадратного уравнения отрицательные,
if ( y1<0 && y2<0)
//вывод сообщения "Корней нет"
cout<<" Нет действительных корней \ n ";
//Если оба корня квадратного уравнения положительные,
else if ( y1>=0 && y2>=0)
{ //Вычисление четырёх корней биквадратного уравнения
x1=sqrt ( y1 );
x2=-x1;
x3=sqrt ( y2 );
x4=- sqrt ( y2 );
//Вывод корней уравнения на экран .
cout<<" \t X1 = "<<x1<<" \t X2 = "<<x2;
cout<<" \t X3 = "<<x3<<" \t X4 = "<<x4<<" \n ";
}
//Если не выполнились условия
// 1.y1<0 и y2<0
// 2.y1>=0 и y2>=0,
//то проверяем условие y1>=0.
else if ( y1>=0) //Если оно истинно
{ //вычисляем два корня биквадратного уравнения.
x1=sqrt ( y1 );
x2=-x1;
cout<<" X1 = "<<x1<<" \t X2 = "<<x2<<" \n ";
}
else
{ //Если условие y1>=0 ложно, то вычисляем два корня биквадратного уравнения
x1=sqrt ( y2 );
x2=-x1;
cout<<" X1 = "<<x1<<" \t X2 = "<<x2<<" \n ";
}
}
return 0;
}
Читателю предлагается самостоятельно модифицировать программу таким образом, чтобы она находила все корни (как действительные, так и комплексные) биквадратного уравнения.