|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Операторы управления
Задача 3.6. Составить программу для решения кубического уравнения 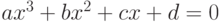 .
.
Кубическое уравнение имеет вид
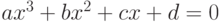 |
( 3.1) |
После деления на a уравнение 3.1 принимает канонический вид:
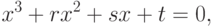 |
( 3.2) |
где 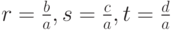 .
.
В уравнении 3.2 сделаем замену  и получим приведённое уравнение:
и получим приведённое уравнение:
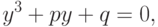 |
( 3.3) |
где 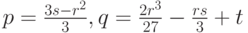 .
.
Число действительных корней приведённого уравнения (3.3) зависит от знака дискриминанта (табл. 3.1)  .
.
| Дискриминант | Количество действительных корней | Количество комплексных корней |
|---|---|---|
 |
1 | 2 |
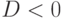 |
3 | - |
Корни приведённого уравнения могут быть рассчитаны по формулам Кардано:
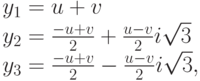 |
( 3.4) |
где ![u=\sqrt[{3}]{\frac{-q}{2}+\sqrt{D}},v=\sqrt[{3}]{\frac{-q}{2}-\sqrt{D}}](/sites/default/files/tex_cache/7c6085d680fdc96c6fadda9cd77d3950.png) .
.
При отрицательном дискриминанте уравнение (3.1) имеет три действительных корня, но они будут вычисляться через вспомогательные комплексные величины. Чтобы избавиться от этого, можно воспользоваться формулами:
![\begin{array}{l} y_1=2\sqrt[{3}]{\rho}\cos(\frac{\phi}{3}),\\ y_2=2\sqrt[{3}]{\rho}\cos(\frac{\phi}{3}+\frac{2\pi}{3}),\\ y_3=2\sqrt[{3}]{\rho}\cos(\frac{\phi}{3}+\frac{4\pi}{3}), \end{array}](/sites/default/files/tex_cache/4c3e76bf1a729effc8529d49e808fca5.png) |
( 3.5) |
где 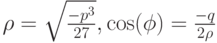 .
.
Таким образом, при положительном дискриминанте кубического уравнения (3.3) расчёт корней будем вести по формулам (3.4), а при отрицательном — по формулам (3.5). После расчёта корней приведённого уравнения (3.3) по формулам (3.4) или (3.5), необходимо по формулам
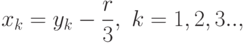
перейти к корням заданного кубического уравнения (3.1).
Блок-схема решения кубического уравнения представлена на рис. 3.18.
Описание блок-схемы. В блоке 1 вводятся коэффициенты кубического уравнения, в блоках 2–3 рассчитываются коэффициенты канонического и приведённого уравнений. Блок 4 предназначен для вычисления дискриминанта. В блоке 5 проверяется знак дискриминанта кубического уравнения. Если он отрицателен, то корни вычисляются по формулам 3.5 (блоки 6–7). При положительном значении дискриминанта расчёт идёт по формулам 3.4 (блок 9, 10). Блоки 8 и 11 предназначены для вывода результатов на экран.
Текст программы с комментариями приведён ниже3При расчёте величин  и
и  в программе предусмотрена проверка значения подкоренного выражения. Если
в программе предусмотрена проверка значения подкоренного выражения. Если  , то
, то ![u=\sqrt[{3}]{\frac{-q}{2}+\sqrt{D}}](/sites/default/files/tex_cache/edafc5f9fdbc366f418a68091e685579.png) , а
, а ![v=\sqrt[{3}]{\frac{-q}{2}-\sqrt{D}}](/sites/default/files/tex_cache/ba6579f48fac2d294793e5ce22f9dba9.png) .Если
.Если  , то
, то ![u=\sqrt[{3}]{|\frac{-q}{2}+\sqrt{D}|}](/sites/default/files/tex_cache/bfdb4d83de73f82c658e3460626d606d.png) , а
, а ![v=\sqrt[{3}]{|\frac{-q}{2}-\sqrt{D}|}](/sites/default/files/tex_cache/7347879ed9ca1538d703acfab4e6df24.png) . Соответственно, при нулевом значении подкоренного выражения u и v обращаются в ноль.
. Соответственно, при нулевом значении подкоренного выражения u и v обращаются в ноль.
#include <iostream>
#include <math.h>
using namespace std;
#define pi 3.14159 //Определение константы
int main ( )
{
float a, b, c, d,D, r, s, t, p, q, ro, fi, x1, x2, x3, u, v, h, g;
//Ввод коэффициентов кубического уравнения.
cout<<" a = "; cin >>a;
cout<<" b = "; cin >>b;
cout<<" c = "; cin >>c;
cout<<" d = "; cin >>d;
//Расчёт коэффициентов канонического уравнения по формуле 3.2
r=b/a; s=c /a; t=d/a;
//Вычисление коэффициентов приведённого уравнения по формуле 3.3
p=(3*s -r * r ) / 3; q=2* r* r * r /27 - r * s/3+t;
//Вычисление дискриминанта кубического уравнения
D=(p /3) * ( p /3) * ( p /3) +(q /2) * ( q /2);
if (D<0)
{
//Формулы 3.5
ro=sqrt ( ( float )( -p* p* p/27) );
fi=-q /(2 * ro );
fi=pi/2 - atan ( fi / sqrt (1 - fi * f i ) );
x1=2*pow( ro, ( float ) 1/3) * cos ( f i /3)- r /3;
x2=2*pow( ro, ( float ) 1/3) * cos ( f i /3+2* pi /3)- r /3;
x3=2*pow( ro, ( float ) 1/3) * cos ( f i /3+4* pi /3)- r /3;
cout<<" \n x1 = "<<x1<<" \t x2 = "<<x2;
cout<<" \t x3 = "<<x3<<" \n ";
}
else
{
//Формулы 3.4
if ( -q/2+sqrt (D) >0) u=pow(( - q/2+sqrt (D) ),( float ) 1/3);
else
if ( -q/2+sqrt (D) <0) u=-pow( fabs( -q/2+sqrt (D) ),( float ) 1/3);
else u=0;
if (-q/2 - sqrt (D) >0) v=pow(( -q/2 - sqrt (D) ),( float ) 1/3);
else
if ( -q/2 - sqrt (D) <0) v=-pow( fabs( -q/2 - sqrt (D) ),( float ) 1/3);
else v=0;
x1=u+v-r /3; //Вычисление действительного корня кубического уравнения.
h= -(u+v)/2 - r /3; //Вычисление действительной
g=(u-v) /2 -sqrt (( float ) 3); //и мнимой части комплексных корней
cout<<" \ n x1 = "<<x1;
if (x2>=0)
{
cout<<x1<<" + "<<x2<<" i \t ";
cout<<x1<<" -"<<x2<<" i \n ";
}
else
{
cout<<x1<<" -"<<fabs ( x2 )<<" i \t ";
cout<<x1<<" + "<<fabs ( x2 )<<" i \n ";
}
}
if (g>=0)
{
cout<<" \t x2 = "<<h<<" + "<<g<<" i ";
cout<<" \t x3 = "<<h<<" -"<<g<<" i \n ";
}
else
{
cout<<" \t x2 = "<<h<<" -"<<fabs (g)<<" i ";
cout<<" \t x2 = "<<h<<" + "<<fabs (g)<<" i ";
}
return 0;
}

