Операторы управления

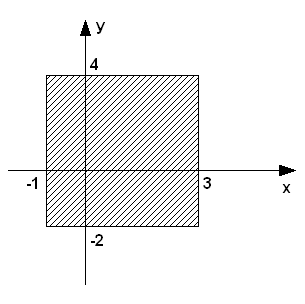
Задача 3.2. Даны вещественные числа и . Определить, принадлежит ли точка с координатами (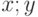) заштрихованной области (рис. 3.12).

Рис. 3.12. Графическое представление задачи 3.2

Рис. 3.13. Алгоритм решения задачи 3.2

Как показано на рис. 3.12, область ограничена линиями и . Значит точка с координатами (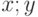) будет принадлежать этой области, если будут выполняться следующие условия: и 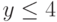. Иначе точка лежит за пределами области.

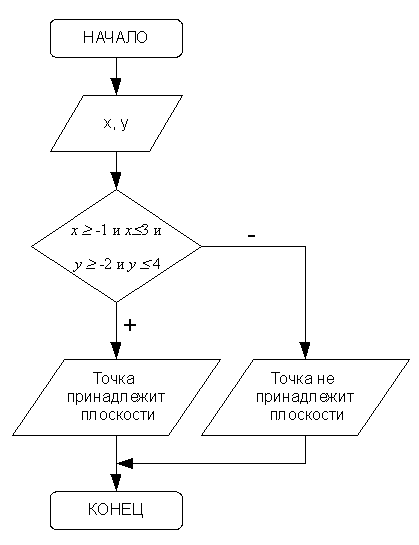
Блок-схема, описывающая алгоритм решения данной задачи, представлена на рис. 3.13.

Текст программы к задаче 3.2:

#include <iostream>
using namespace std;
int main ( )
{ float X,Y;
	cout<<" X = "; cin >>X;
	cout<<" Y = "; cin >>Y;
	if (X>=-1 && X<=3 && Y>=-2 && Y<=4)
	cout <<"Точка принадлежит области"<< endl;
	else
	cout<<"Точка не принадлежит области"<<endl;
	return 0;
}
			

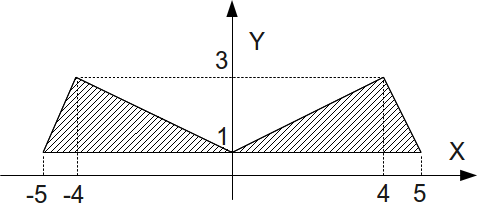
Задача 3.3. Даны вещественные числа и . Определить, принадлежит ли точка с координатами (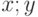) заштрихованной области (рис. 3.14).

Составим уравнения линий, ограничивающих заданные области. В общем виде уравнение прямой, проходящей через точки с координатам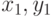и () и (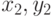), имеет вид:

Рис. 3.14. Графическое представление задачи 3.3

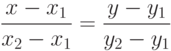
Треугольник в первой координатной области ограничен линиями, проходящими через точки:

1. (0, 1) - (4, 3);
2. (4, 3) - (5, 1);
3. (5, 1) - (0, 1).

Следовательно, уравнение первой линии:

уравнение второй линии:

и уравнение третьей линии: .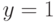

Линии, которые формируют треугольник во второй координатной области, проходят через точки:

1. (0, 1) - (-4, 3);
2. (-4, 3) - (-5, 1);
3. (-5, 1) - (0, 1);

Следовательно, уравнение первой линии:

уравнение второй линии:

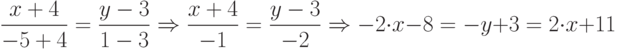
и уравнение третьей линии: .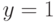

Таким образом, условие попадания точки в заштрихованную часть плоскости имеет вид:

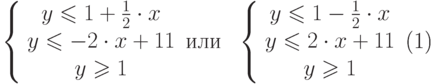
Далее приведён текст программы для решения задачи 3.3.

#include <iostream>
using namespace std;
int main ( )
{
	float X,Y;
	cout<<" X = "; cin >>X;
	cout<<" Y = "; cin >>Y;
	if ( (Y<=1+( float ) 1/2 *X && Y<=-2*X+11 && Y>=1) | | (Y<=1-( float ) 1/2 *X && Y<=2*X+11 && Y>=1))
		cout <<"Точка принадлежит области"<< endl;
	else
		cout<<"Точка не принадлежит области"<< endl;
	return 0;
}