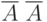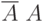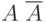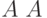Формула Бернулли. Формула Пуассона. Наивероятнейшее число наступления событий. Локальная теорема Муавра-лапласса
Рассмотрим пример. Пусть Некто бросил монетку два раза. Считая каждый исход "орел" - "решка" равновероятным и независимым от предыдущего результата, получим следующие варианты результатов:
![\[ \overline A \ \overline A, \overline A \ A, \ A \ \overline A, \ A \ A \]](/sites/default/files/tex_cache/af0cd79c781b239bbd3a7a448d37bf01.png)
где обозначено появление 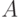 - "решки" и
- "решки" и 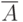 - "орла". Понятно, что при этом
- "орла". Понятно, что при этом 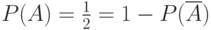 , так как появление "орла" или "решки" события равновероятные. Для удобства введем обозначение
, так как появление "орла" или "решки" события равновероятные. Для удобства введем обозначение 
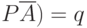 . Очевидно, что
. Очевидно, что 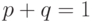 .
.
Пусть теперь монету кидают 3 раза. Теперь возможны 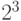 разных вариантов исходов:
разных вариантов исходов:
![\[ \overline A \ \overline A \ \overline A , \ \overline A \ \overline A \ A \ , \overline A \ A \ \overline A, \ A \ \overline A \ \overline A, \ \overline A \ A \ A, \ A \ \overline A \ A, \ A \ A \ \overline A , \ A \ A \ A \]](/sites/default/files/tex_cache/283459a61580bd3bc5032274f245cfc4.png)
Можно убедиться самостоятельно, что, если монетку кидать 4 раза, то получится  различных вероятных комбинаций.
различных вероятных комбинаций.
Рассуждая далее, имеем, что в случае 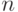 испытаний Некто получит одну из
испытаний Некто получит одну из 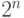 комбинаций исходов.
комбинаций исходов.
Так как испытания независимые, то, применяя теорему умножения вероятностей найдем вероятности каждого из проведенных испытаний (табл. 5.1 для 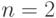 ; табл. 5.2 для
; табл. 5.2 для 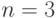 ).
).
| Исход | Вероятность | Исход | Вероятность | Исход | Вероятность | Исход | Вероятность |
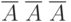 |
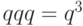 |
 |
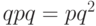 |
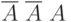 |
 |
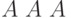 |
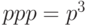 |
 |
 |
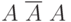 |
 |
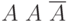 |
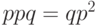 |
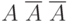 |
 |
Проанализируем табл. 5.2 более подробно. Заметим, что не появление события А во всех трех испытаниях имеет вероятность  , соответствующую только одному единственному исходу
, соответствующую только одному единственному исходу 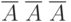 . Тогда вероятность, появления события А один раз соответствует (см. табл. 3)
. Тогда вероятность, появления события А один раз соответствует (см. табл. 3)
![\[ P_{3}(1)=P\left (\overline A \overline A \ \overline A \right ) + P\left (\overline A \ A \ \overline A \right ) + P\left (\overline A \ \overline A \ A \right ) =3pq^2 \]](/sites/default/files/tex_cache/ad7cd7ba5ed14cea5ba86b6c89a6914d.png)
Аналогично, вероятность появления 2-х раз А будет равна .
![\[ P_{3}(2)=P\left (\overline A \ A \ \ A \right ) + P\left (A \ \overline A \ A \right ) + P\left (A \ A \ \overline A \right ) =3p^2q \]](/sites/default/files/tex_cache/08060e59d1c5f32ebebb402038140a0f.png)
И, наконец, если событие А состоялось все три раза, то
![\[ P_{3}(3)=P\left (A \ A \ A ) =p^3. \]](/sites/default/files/tex_cache/63c84e468430dd1fec9dfbb7b5a34934.png)
Можно убедиться, что эти события образуют полную группу, т.е.
![\[ P_{3}(0) + P_{3}(1) + P_{3}(2) + P_{3}(3) =q^3+3pq^2+3p^2q+p^3= (p+q)^3=1. \]](/sites/default/files/tex_cache/21f3d13819474cce7c93901cf33abd7b.png)
Если рассмотреть вероятность  , вероятность появления собы-тия А m раз в n испытаниях, то, рассуждая так, как это было представлено ранее получим формулу
, вероятность появления собы-тия А m раз в n испытаниях, то, рассуждая так, как это было представлено ранее получим формулу
![\[P_{m,n}=C_{n}^m p^mq^{n-m} \]](/sites/default/files/tex_cache/c4e3e92d4cb7ecdf634bf16b6ba13a2d.png) |
( 1) |
которая известна как формула Бернулли.Эта формула определяет вероятность появления события А 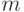 раз в
раз в 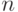 испытаниях. В формулу входит коэффициент
испытаниях. В формулу входит коэффициент 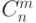 , который читается как число сочетаний из
, который читается как число сочетаний из 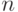 исходов по
исходов по 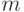 раз. Более коротко число сочетаний из
раз. Более коротко число сочетаний из 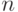 по
по 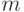 . Вычисляется по простой формуле:
. Вычисляется по простой формуле: 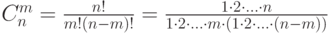
Пример 1. В ящике лежат 20 белых и 10 черных шара. 4 раза извлекали шар, причем после каждого раза взятый шар возвращался в ящик и все шары тщательно перемешивались. Найти вероятность того, что 2 раза из 4-х был извлечен белый шар.
Решение. Решим задачу двумя способами.
1 способ. Обозначим событие 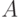 – "вытащили белый шар",
– "вытащили белый шар", 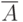 - "вытащили черный шар". Тогда рассмотрим все возможные комбинации появления шаров. Таких комбинаций будет
- "вытащили черный шар". Тогда рассмотрим все возможные комбинации появления шаров. Таких комбинаций будет  :
:
![\[ A \ A \ A \ A; \ A \ A \ A \ \overline A; \ A \ A \overline A \ A; \ A \ \overline A \ A \ A; \ \overline A \ A \ A \ A; \ \overline A \ \overline A \ A \ A; \ A \ \overline A \ \overline A \ A; \ A \ A \ \overline A \ \overline A; \ \\ \overline A \ A \ A \ \overline A; \ \overline A \ A \ \overline A \ A; \ A \ \overline A \ A \ \overline A; \overline A \ \overline A \ \overline A \ A; \ A \ \overline A \ \overline A \ \overline A; \ \overline A \ A \ \overline A \ \overline A; \ \overline A \ \overline A \ A \ \overline A; \ \overline A \ \overline A \ \overline A \ \overline A. \]](/sites/default/files/tex_cache/3cee9acf3660e5d674010672dabc6c5c.png)
Нас интересуют только те исходы, в которых появляются по 2 раза белые и черные шары. Всего таких исходов 6. Вероятность вытащить белый шар  в каждом из испытаний, так как по условию задачи шарик после испытания возвращается в ящик. Аналогично вычисляем вероятность извлечения черного шарика
в каждом из испытаний, так как по условию задачи шарик после испытания возвращается в ящик. Аналогично вычисляем вероятность извлечения черного шарика  . Подсчитаем теперь искомую вероят-ность:
. Подсчитаем теперь искомую вероят-ность: 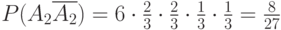 ,
,
где 6 - количество благоприятных исходов;  - вероят-ность появления белого шара в любых 2-х испытаниях;
- вероят-ность появления белого шара в любых 2-х испытаниях;  - вероятность появления черного шара в любых 2-х испытаниях.
- вероятность появления черного шара в любых 2-х испытаниях.
2 способ. Для решения воспользуемся формулой Бернулли (1):
![\[P_{2,4}=C_{4}^2 p^2q^2=\frac {4!} {2! (4-2)!} \cdot \left ( \frac 2 3 \right )^2 \cdot \left ( \frac 1 3 \right )^2 = \frac {2 \cdot 3 \cdot 4 \cdot 2 \cdot 2} {2 \cdot 2 \cdot 3 \cdot 3 \cdot 3 \cdot 3}= \frac 8 {27}.\]](/sites/default/files/tex_cache/a96181cc9bba7b8dae723f8adb997677.png)
Как видим ответы совпадают, однако первый способ не всегда удобен в применении. Особенно, если речь идет о значительном количестве испытаний.
Пример 2. Вероятность попадания стрелка в цель 0,8. Стрелок делает 10 выстрелов. Найти вероятность, что цель будет поражена 8 раз.
Решение. Для решения задачи воспользуемся формулой Бернулли:
![\[ P_{8,10}=C_{10}^8 p^8q^2=\frac {10!} {8! (10-8)!} \cdot (0,8)^8 (0,2)^2 = \frac {9 \cdot 10} 2 \cdot \frac {4^8} {5^8} \cdot \frac 1 {5^2} \approx 0,3.\]](/sites/default/files/tex_cache/db1f2f1b661db9f5140e761320b63ec5.png)
Можно легко убедиться в справедливости следующих равенств:
![\[P_{0,n}=q^n; \ P_{n,0} = p^n; \ P_{1,n}=n \cdot p \cdot q^{1-n}; \ P_{2,n}=\frac {n(n-1)} 2 p^2 q^{n-2}.\]](/sites/default/files/tex_cache/dd63caffaf01f586d7610c986a6d1b72.png)
Все эти формулы являются частным случаем формулы (1).
При 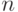 испытаниях некоторое событие, имеющее вероятность
испытаниях некоторое событие, имеющее вероятность 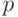 может появиться несколько раз, однако, если обозначить
может появиться несколько раз, однако, если обозначить  - наименьшее количество раз появление некоторого события при
- наименьшее количество раз появление некоторого события при 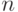 испытаниях, то получим
испытаниях, то получим
![\[P_{m_{0},n}=C_{n}^{m_{0}} p^{m_{0}}q^{n-m_{0}} .\]](/sites/default/files/tex_cache/cd0ba6015979540398d927b0d64ec1d8.png) |
( 2) |
Очевидно, что 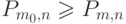 выполняется при
выполняется при 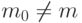 , т.е.
, т.е.  - это гарантированное число появлений события при
- это гарантированное число появлений события при 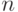 испытаниях. Иными словами, появление события большее количество раз или меньшее будет менее вероятным, чем
испытаниях. Иными словами, появление события большее количество раз или меньшее будет менее вероятным, чем  . Если
. Если  и
и 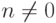 , тогда можно записать
, тогда можно записать
![\[ np-q \leqslant m_{0} \leqslant np+p .\]](/sites/default/files/tex_cache/6283dd8e4363ea44da1556f27bc7e380.png) |
( 3) |
где  - наивероятнейшее число появления события А при
- наивероятнейшее число появления события А при 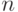 испытаниях;
испытаниях; 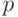 - вероятность появления события А при одном испытании;
- вероятность появления события А при одном испытании; 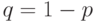 .
.
Если 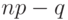 и
и 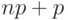 не целые числа, то тогда они округляются до ближайшего целого, но так, чтобы интервал не увеличивался.
не целые числа, то тогда они округляются до ближайшего целого, но так, чтобы интервал не увеличивался.