Основы теории вероятностей
[+]
Опубликован: 28.04.2012 | Доступ: свободный | Студентов: 3108 / 892 | Оценка: 3.86 / 2.57 | Длительность: 07:45:00
Тема: Математика
Специальности: Математик, Преподаватель
Теги: beta, анализ, биноминальное распределение, бифуркация, вычисления, графика, дискретная случайная величина, законы, несовместное событие, нормальная функция, ось ординат, полная группа, распределение пуассона, формула полной вероятности, цвета, элементарное события
Практическая работа 1:

Классическое определение вероятности. Теорема сложения вероятностей
A
|
версия для печати
< Лекция 1 || Практическая работа 1 || Лекция 2 >
Аннотация: Задачи и примеры их решения.
Ключевые слова: ПО, вероятность, группа, выражение, место, работ, безопасность, анализ, выборка, радиус, площадь, интервал

Примеры решения задач

Задача 1.В коллекцию было отобрано по 13 образцов с четырех месторождений, и каждый образец был пронумерован от 1 до 13. Из ящика, где хранились образцы, при оформлении экспозиции наудачу вынимают три образца. Найти вероятность того, что эти образцы имеют номера 3, или 7, или 13.

Решение. Так как месторождений 4, то каждой цифры в нумерации образцов будет 4, следовательно, всего было использовано $13 \cdot 4 = 52$ номера. Из общего количества номеров по условию задачи нас интересуют только три, значит, всего таких номеров будет $3 \cdot 4 = 12$. Тогда по классическому определению вероятностей вероятность выбора любого из указанных номеров будет равна $P(A)=\frac {12} {52} =\frac 3 {13} \approx 0,24 $. Это вероятность того, что среди выбранных образцов будут образцы, имеющие только выбранные номера. Если задаться вопросом, какова вероятность того, что будут присутствовать все номера, тогда задача будет решаться иначе.

Подсчитаем количество вариантов выбора образцов. Т.к. нам надо три образца, а всего номеров 52, то количество вариантов выбора будет 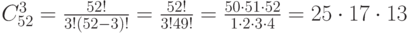$C_{52}^{3}=\frac {52!} {3!(52-3)!}=\frac {52!} {3!49!} = \frac {50 \cdot 51 \cdot 52} {1 \cdot 2 \cdot 3 \cdot 4} = 25 \cdot 17 \cdot 13$ С другой стороны, предположим, что из каждой группы номеров 3, 7 и 13 выбрано только по 1 номеру. Таких вариантов будет $\frac {4} {12} \cdot \frac {4} {11} \cdot \frac {4} {10}$. Знаменатель уменьшается, так как при выборе одного образца общее количество образцов интересуемой нас группы уменьшается на 1. Так как номера равновероятны, то группа может начинаться с 3, или с 7, или с 13, поэтому последнее выражение должно быть умножено на 3 – количество разнообразия. Теперь можно подсчитать вероятность выбора всех номеров:

\[ P(B)=\frac {\frac {4} {12} \cdot \frac 4 {11} \cdot \frac 4 {10} \cdot 3} {25 \cdot 17 \cdot 13} =\frac 8 {55 \cdot 25 \cdot 17 \cdot 13}\]
Т.е. вероятность очень мала.

Задача 2.Вокруг костра расположились на привале 5 геологов и 5 рабочих, нанятых в поселке. Какова вероятность того, что 2 геолога или 2 рабочих не сидят рядом, если места занимались случайно?

Решение. Пронумеруем все места вокруг костра. Для того, чтобы выполнить условия задачи геологи должны занять либо четные, либо нечетные места, тогда рабочие займут остальные. 5 геологов могут занять 5 четных мест 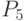$P_{5}$ способами, тогда рабочие рассядутся 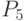$P_{5}$ способами на нечетные места. Всего способов рассадить геологов и рабочих, очевидно, будет $P_{5} \cdot P_{5} = P_{5}^2$, если первое место у геологов четное. Если же первое место нечетное, то будет столько же вариантов. Значит, всего способов рассадить людей по условию задачи существует $2 \cdot (P_{5})^2$. Совершенно очевидно, что общее количество вариантов рассадить людей вокруг костра будет $P_{10}$. Таким образом, вероятность, что 2 геолога или 2 рабочих не сидят рядом будет:

\[ P(A)=\frac {2 \cdot (P_{5})^2} { P_{10}} = \frac {2 \cdot 5! \cdot 5!} {10!} = \frac {2 \cdot 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5} {6 \cdot 7 \cdot 8 \cdot 9 \cdot 10} =\frac 1 {126}.\]

Задача 3 На столе лежат 36 образцов с номерами 1, 2, 3, …, 36. Лаборант берет 3 любых образца. Какова вероятность того, что у них номера будут из первой четверки номеров?

Решение. Всего лаборант может выбрать образцы $C_{36}^{3}$ способами. Из первой четверки номеров выбрать 3 образца можно $C_{4}^{3}$ способами, следовательно вероятность того, что номера образцов будут из первой четверки номеров будет равна

\[ P(A)=\frac { C_{4}^{3}} { C_{36}^{3}} = \frac {3! \cdot 33! \cdot 4!} {36! \cdot 3! \cdot 1!} = \frac {1 \cdot 2 \cdot 3 \cdot 4} {34 \cdot 35 \cdot 36} = \frac 1 {17 \cdot 35 \cdot 3} \approx 0,001.\]

Эту задачу можно решить иначе. Вероятность выбрать первый образец из группы с номерами от 1 до 4 равна, очевидно, $\frac {4} {36}$. Вероятность выбрать второй образец из той же группы равна уже $\frac {3} {35}$, т.к. считаем, что образец был взят из первой группы, следовательно, в группе для выбора осталось только 3 номера; общее количество образцов уменьшилось на 1, потому что был выбран 1 образец. Тогда вероятность выбора третьего образца из первой группы будет, очевидно по тем же соображениям, равна $\frac {2} {34}$. Все три события должны произойти обязательно, т.е. все три образца должны быть с номерами от 1 до 4 (по условию), значит, вероятность такого выбора будет: $P(A)= \frac {4} {36} \cdot \frac {3} {35} \cdot \frac {2} {34} = \frac {1} {3 \cdot 35 \cdot 17} \approx 0,001$. Как видим, результат равен результату, подсчитанному иным способом.

Задача 4.При проведении буровзрывных работ было заложено 3 заряда. Вероятность самопроизвольного взрыва первого заряда 0,01, второго 0,008, третьего 0,025. При взрыве одного заряда от детонации взрываются два других. Найти вероятность того, что заряды взорвутся.

Решение.Для того, чтобы найти вероятность самопроизвольного взрыва, необходимо знать какие ситуации могут быть. Для этого составим таблицу возможных исходов:

Тестовая таблица
Заряд 1 2 3 4 5 6 7 8
1-й заряд - + - - + - + +
2-й заряд - - + - + + - +
3-й заряд - - - + - + + +

В таблице знаком "+ " обозначен самопроизвольный взрыв заряда. Всего вариантов 8. По условию задачи нам подходят варианты со 2-го по 8. Однако, выбор одного из вариантов полностью исключает выбор другого, поэтому вероятность самопроизвольного взрыва будет равна: $P(A)=P(2)+P(3)+\cdots +P(8)$. Следовательно, если обозначить $p_{i}$ - вероятность самопроизвольного взрыва -го заряда (в таблице "+ "), а $\overline {p_{i}}$ - вероятность, что -ый заряд самопроизвольно не взорвется (в таблице "-"), тогда искомую вероятность можно расписать:

\[ P(A)=p_{1} \cdot \overline {p_{2}} \cdot \overline {p_{3}} + p_{2} \cdot \overline {p_{1}} \cdot \overline {p_{3}} + p_{3} \cdot \overline {p_{1}} \cdot \overline {p_{2}} + p_{1} \cdot p_{2} \cdot \overline {p_{3}}+ p_{1} \cdot p_{3} \cdot \overline {p_{2}} + p_{2} \cdot p_{3} \cdot \overline {p_{1}}+ p_{1} \cdot p_{2} \cdot p_{3}.\]

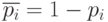Вероятности $\overline {p_{i}}$ определяем, используя известное свойство: $ p_{i}+ \overline {p_{i}} =1$, т.е. $ \overline {p_{i}} =1 - p_{i} $. С учетом сказанного получаем: 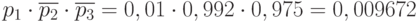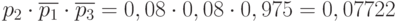$ p_{1} \cdot \overline {p_{2}} \cdot \overline {p_{3}} =0,01 \cdot 0,992 \cdot 0,975 = 0,009672$, $ p_{2} \cdot \overline {p_{1}} \cdot \overline {p_{3}} =0,08 \cdot 0,08 \cdot 0,975 = 0,07722$, …, и тогда в итоге получим:

\[ P(A)=0,009672 + 0,07722 +0,024552 +0,000078 +0,000198 +0,000248 +0,000002 =0,04247.\]

Не всегда можно так просто, как в данном примере, подсчитать количество вариантов. Но тогда можно предложить немного иной способ решения подобных задач. Если внимательно проанализировать таблицу вариантов, то можно увидеть, что только один вариант, когда все три заряда не взорвались, обеспечивает безопасность, т.е. исключает вероятность самопроизвольного взрыва. 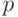Зная, что $ p+ \overline {p} =1$ и, обозначив за $p$ - вероятность самопроизвольного взрыва 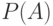$P(A)$, получим, такой же ответ:

\[ P(A)=1- \overline p = 1- 0,99 \cdot 0,992 \cdot 0,975 \approx 0,042.\]

Задача 5.В экспедицию отправлено 17 специалистов и 8 студентов. Какова вероятность того, что в списке последней окажется фамилия студента?

Решение. Всего в списке будет находиться 25 фамилий членов экспедиции. Нас интересует одно конкретное место, одно из 25 возможных. Это место могут занять 8 из 25 членов экспедиции, следовательно вероятность того, что в списке последней окажется фамилия студента будет равна $P(A)=\frac 8 {25} = 0,32$.

Задача 6.На анализ в химическую лабораторию привезли 1000 образцов. После анализа оказалось, что один образец содержит золото, 10 – серебро, 50 – цинк, 100 – медь, в остальных образцах ничего, заслуживающего внимания, не нашли. Лаборант берет один из образцов на повторный анализ. Какова вероятность того, что в образце будет содержаться цинк или медь?

Решение.Всего привезли 1000 образцов, образцов с цинком и медью было 50+100=150. Следовательно, вероятность извлечь требуемый образец будет равна: 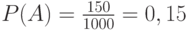$P(A)=\frac {150} {1000} = 0,15$.

Задача 7.В ящике с образцами находятся 90 уже распиленных образцов и 10 не распиленных. Найти вероятность того, что из 10 наугад взятых образцов все будут распиленные (образцы извлекаются одновременно).

Решение.Так как образцы извлекаются одновременно, то в выборку из 10 образцов, общее разнообразие выборок будет равно $C_{100}^{10}$, если положить, что все образцы различаются, хотя бы номерами. По условию задачи, нас интересует выборка из распиленных образцов, общее разнообразие которой будет $C_{90}^{10}$. Таким образом вероятность того, что из 10 наугад взятых образцов все будут распиленные, если образцы извлекаются одновременно, будет равна:

\[ P(A)=\frac { C_{90}^{10}} { C_{100}^{10}} = \frac {90! \cdot 10! \cdot (100-10)!} {10! \cdot (90-10)! \cdot 100!} = \cdots \approx 0,33.\]

Задача 8.Все образцы в ящике пронумерованы от 1 до 100. Наудачу извлекли образец. Какова вероятность того, что квадрат номера этого образца будет оканчиваться цифрой 1?

Решение.Условие задачи будет выполняться в том случае, если на конце цифры будут стоять 1 или 9. Поэтому в каждом десятке таких цифр будет 2. Например, 11 и 19; 21 и 29 и т.д. Поэтому подсчитать общее количество таких цифр не представляет труда: $2 \cdot 10=20$. Вероятность того, что квадрат номера взятого образца будет оканчиваться цифрой 1, будет равна: $P(A)=\frac {20} {100} = 0,2$.

Задача 9.На экзамене студенту предлагаются 3 вопроса из 60. Из вопросов, предлагаемых на экзамене, студент знает 50. Какова вероятность того, что предложенный студенту вариант, будет состоять из известных ему вопросов?

Решение.Три вопроса предлагаются одновременно, поэтому подсчитаем количество возможных вариантов заданий: $C_{60}^{3}$. Тогда количество вариантов, на которые бы студент смог ответить будет равно: $C_{50}^{3}$. Пользуясь классическим определением вероятности получаем, что вероятность того, что предложенный студенту вариант, будет состоять из известных ему вопросов будет равна:

\[ P(A)=\frac { C_{50}^{3}} { C_{60}^{3}} = \frac {50! \cdot 3! \cdot (60-3)!} {3! \cdot (50-3)! \cdot 60!} = \cdots \approx 0,57.\]

Задача 10.На карте параллели находятся друг от друга на расстоянии 2а. На карту упала монета, имеющая радиус $r < a$. Какова вероятность того, что монета не пересечет ни одну из параллелей?

Решение.Данная задача решается геометрическим способом. Выполним для начала чертеж задачи.

Чертеж задачи 10

Рис. 2.1. Чертеж задачи 10
Очевидно, что монета пересечет линию, если ее центр попадет в не заштрихованную область чертежа. Тогда вероятность того, что монета не пересечет ни одну из параллелей, будет равна отношению площади всей области к площади не заштрихованной:
\[ P(A)=\frac {S_{Y}} {S_{об}} = \frac {2al – 2rl} {2al} =1-\frac {r} {a}.\]

Задача 11.На карте, лежащей на столе, была выделена область в виде эллипса $\frac {x^2} {a^2} + \frac {y^2} {b^2} = 1$, а в ней - еще 5 подобластей в виде кружочков радиусом а/10. С потолка на карту падает капля. Если капля падает в область, ограниченную эллипсом, то найти вероятность того, что она (капля) не попадет в кружочки. Считать при решении задачи, что капля слишком маленькая (размерами капли можно пренебречь), а границы эллипса и кружочков не пересекаются.

Решение.Данная задача решается геометрическим способом. Выполним для начала чертеж задачи.

Чертеж задачи 11

Рис. 2.2. Чертеж задачи 11

Очевидно, что и в этом случае, вероятность находится отношением площади незаштрихованной части эллипса к площади всего эллипса. Площадь кружочков будет равна: $S_{k}=5 \cdot \pi \cdot \left (\frac a {10} \right )^2 = \frac {\pi a^2} {20}$. Площадь эллипса равна $S_{э}= \pi \cdot a \cdot b $. Тогда вероятность того, что капля не попадет в кружочки, будет равна: $S_{k}=\frac { S_{э} - S_{k}} {S_{э}}=1 - \frac {\pi a^2} {20 \cdot \pi \cdot a \cdot b } = 1 - \frac {a} {20 \cdot b }. $

Задача 12.Для того чтобы некоторое устройство отказало в работе, надо, чтобы два управляющих сигнала поступили в приемник этого устройства с интервалом меньше 0,02 ч. Найти вероятность того, что устройство откажет с 22.00 по 22.15. Сигналы считать равнозначными.

Решение.Данная задача решается геометрическим способом. Выполним для начала чертеж задачи.

Чертеж задачи 12

Рис. 2.3. Чертеж задачи 12

Построим квадрат времени, сторона которого будет равна требуемому периоду, т.е. 15 мин. Предположим, что второй сигнал поступил. Тогда рассуждаем так. Первый сигнал может поступить в любой момент из этих 15 минут, но нас интересует интервал времени 0,02 часа = 1,2 мин. Точка С на рисунке отмечен данный интервал. Если сигнал поступит не позже, чем 1,2 мин, после второго сигнала, то устройство откажет. Следовательно, многоугольник 22АВС – это время, в которое после поступление первого сигнала, второго устройство откажет. Рассуждая аналогично, и предположив, что поступил сигнал от второго устройства, получим вторую часть многоугольника - 22DEA. Таким образом, устройство откажет, если момент поступления сигналов будет располагаться внутри данного многоугольника – 22ABCDE.

Подсчитаем площади: Общая площадь квадрата равна $15 \cdot 15 =225 (мин)^2$. Площадь многоугольной области будет равна $15 \cdot 15 -(15-1,2) \cdot (15-1,2)=225 - 190,44 =34,56 (мин)^2$.

Тогда вероятность того, что устройство откажет с 22.00 по 22.15, будет равна: $P(A)=\frac {34,56} {225} = 0,15$

Дальше >>
< Лекция 1 || Практическая работа 1 || Лекция 2 >

Вопросы и ответы

вопросов: 0