НОУ ИНТУИТ | Введение в теорию вероятностей. Лекция 11: Числовые характеристики зависимости

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Новосибирский Государственный Университет

Опубликован: 07.04.2008 | Доступ: свободный | Студентов: 7252 / 1307 | Оценка: 4.56 / 4.32 | Длительность: 16:54:00

Тема: Математика

Специальности: Математик

Теги: алгебра, вычисления, графика, дискретное распределение, замечательный предел, коэффициент асимметрии, несовместное событие, полная группа, распределение бернулли, распределение коши, распределение пуассона, формула полной вероятности, функция Эйлера, цвета, элементы

|

Вам нравится? Нравится 73 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Коэффициент корреляции

Определение 40. Коэффициентом корреляции $\rho(\xi,\eta)$ случайных величин $\xi$ и $\eta$ , дисперсии которых существуют и отличны от нуля, называется число

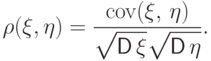
$\rho(\xi,\eta)=\frac{{{\rm cov}}(\xi,\,\eta)}{\sqrt{\vphantom{a^2}{\mathsf D\,}\xi}\sqrt{\vphantom{a^2}{\mathsf D\,}\eta}}.$

Замечание Чтобы разглядеть "устройство" коэффициента корреляции, распишем по определению числитель и знаменатель:

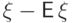$\rho(\xi,\eta)= \frac{{\mathsf E\,}\bigl((\xi-{\mathsf E\,}\xi)(\eta-{\mathsf E\,}\eta)\bigr)} {\sqrt{\vphantom{a^2}{\mathsf E\,}\bigl(\xi-{\mathsf E\,}\xi\bigr)^2} \sqrt{\vphantom{a^2}{\mathsf E\,}\bigl(\eta-{\mathsf E\,}\eta\bigr)^2}}.$

Перед нами - "косинус угла" между двумя элементами $\xi-{\mathsf E\,}\xi$ и $\eta-{\mathsf E\,}\eta$ гильбертова пространства, образованного случайными величинами с нулевым математическим ожиданием и конечным вторым моментом, снабженного скалярным произведением ${{\rm cov}}(\xi,\,\eta)$ и "нормой", равной корню из дисперсии, или корню из скалярного произведения ${{\rm cov}}(\xi,\xi)$ .

Пример 66. Рассмотрим продолжение примера 65, но пусть $\xi$ и $\eta$ будут не только независимыми, но и одинаково распределенными случайными величинами, и их дисперсия отлична от нуля. Найдем коэффициент корреляции величин $\xi$ и $\xi+\eta$ :

$\rho(\xi,\xi+\eta)= \frac{{{\rm cov}}(\xi,\xi+\eta)}{\sqrt{\vphantom{a^2}{\mathsf D\,}\xi}\sqrt{\vphantom{a^2}{\mathsf D\,}(\xi+\eta)}}= \frac{{\mathsf D\,}\xi}{\sqrt{\vphantom{a^2}{\mathsf D\,}\xi}\sqrt{\vphantom{a^2}{\mathsf D\,}\xi+{\mathsf D\,}\eta}} =\frac{{\mathsf D\,}\xi}{\sqrt{\vphantom{a^2}{\mathsf D\,}\xi}\sqrt{\vphantom{a^2}2{\mathsf D\,}\xi}}= \frac{1}{\sqrt{2}}.$

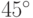Коэффициент корреляции величин $\xi$ и $\xi+\eta$ равен косинусу угла $45^\circ$ , образованного "векторами" $\xi$ и $\xi+\eta$ , когда $\xi$ и $\eta$ "ортогональны" и их "длина" одинакова.

Теорема 33. Коэффициент корреляции обладает свойствами:

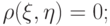
если $\xi$ и $\eta$ независимы, то $\rho(\xi,\eta)=0;$
всегда $|\rho(\xi,\eta)|\le 1;$
$|\rho(\xi,\eta)| = 1$ тогда и только тогда, когда $\xi$ и $\eta$ п.н. линейно связаны, т.е. существуют числа $a\ne 0$ и такие, что ${\Prob(\eta=a\xi+b)=1}$ .

Доказательство. Свойство (1) мы уже много раз ( сколько?) упоминали и один раз доказали. Более того, при рассмотрении свойств математического ожидания мы привели примеры 50 и 51 - два из многих возможных примеров того, что свойство (1) в обратную сторону неверно.

Докажем свойство (2). Рассмотрим преобразование $\widehat \xi=\frac{\xi-{\mathsf E\,}\xi}{\sqrt{{\mathsf D\,}\smash[b]{\xi\mathstrut}}}$ случайной величины, называемое стандартизацией. Случайная величина $\smash[t]{\widehat\xi}\vphantom{\int_c}$ имеет нулевое математическое ожидание и единичную дисперсию:

${\mathsf E\,}\widehat\xi={\mathsf E\,}\frac{\xi-{\mathsf E\,}\xi}{\sqrt{{\mathsf D\,}\smash[b]{\xi\mathstrut}}}= \frac{{\mathsf E\,}\xi-{\mathsf E\,}\xi}{\sqrt{{\mathsf D\,}\smash[b]{\xi\mathstrut}}}=0; \quad {\mathsf E\,}\widehat{\xi}^{\,2}={\mathsf D\,}\widehat\xi= {\mathsf D\,}\frac{\xi-{\mathsf E\,}\xi}{\sqrt{{\mathsf D\,}\smash[b]{\xi\mathstrut}}}= \frac{{\mathsf D\,}(\xi-{\mathsf E\,}\xi)}{{\mathsf D\,}\xi}=1$$

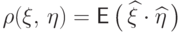Коэффициент корреляции теперь запишется проще: $\rho(\xi,\,\eta)={\mathsf E\,}\bigl(\,\widehat\xi\cdot\widehat\eta\,\bigr)$ . .

Далее, неравенство $(x\pm\mspace{1mu}y)^2\geq 0$ равносильно неравенству

$-\frac12(x^2+y^2)\leq xy\leq \frac12(x^2+y^2).$

Подставив в него $\widehat{\xi}$ вместо

, $\widehat{\eta}$ вместо

и взяв математические ожидания всех частей неравенства, получим свойство (2):

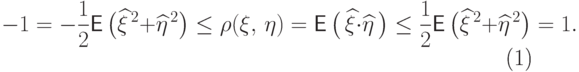$\begin{equation}\label{eq-cov1} -1=-\frac12 {\mathsf E\,}\bigl(\widehat\xi^{\,2}+\widehat\eta^{\,2}\bigr) \leq \rho(\xi,\,\eta)= {\mathsf E\,}\bigl(\,\widehat\xi\cdot\widehat\eta\,\bigr) \leq \frac12 {\mathsf E\,}\bigl(\widehat\xi^{\,2}+\widehat\eta^{\,2}\bigr)=1. \end{equation}$

( 19)

Докажем свойство (3). В одну сторону утверждение проверяется непосредственно: если $\eta=a\xi+b$ , то

$\rho(\xi,\, a\xi+b)= \frac{{\mathsf E\,}(\xi(a\xi+b))-{\mathsf E\,}\xi\cdot{\mathsf E\,}(a\xi+b)} {\sqrt{{\mathsf D\,}\smash[b]{\xi\mathstrut}}\sqrt{\smash[b]{\mathstrut{\mathsf D\,}(a\xi+b)}}}= \frac{a{\mathsf D\,}\xi} {\sqrt{{\mathsf D\,}\smash[b]{\xi\mathstrut}}\sqrt{a^2{\mathsf D\,}\smash[b]{\xi\mathstrut}}}= \begin{cases} \phantom-1, & a>0,\\ -1, & a<0. \end{cases}$

Докажем вторую часть свойства (3): если 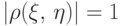$|\rho(\xi,\,\eta)|=1$ , то существуют числа $a\ne 0$ и такие, что $\Prob(\eta=a\xi+b)=1$ .

Рассмотрим сначала случай 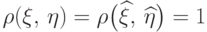$\rho(\xi,\,\eta)=\rho\bigl(\widehat\xi,\,\widehat\eta\bigr)=1$ . Тогда второе неравенство в формуле (19) превращается в равенство:

${\mathsf E\,}\bigl(\widehat\xi\cdot\widehat\eta\bigr)= \frac12 {\mathsf E\,}\bigl(\widehat\xi^{\,2}+\widehat\eta^{\,2}\bigr), \quad\text{т.е.}\quad {\mathsf E\,}\bigl(\widehat\xi-\widehat\eta\bigr)^2=0.$

Если математическое ожидание неотрицательной случайной величины $\smash{\bigl(\widehat\xi-\widehat\eta\bigr)^2}$ равно нулю, то $\bigl(\widehat\xi-\widehat\eta\bigr)^2=0$ , п.н. Поэтому с единичной вероятностью

$\frac{\eta-{\mathsf E\,}\eta}{\sqrt{\mathstrut{\mathsf D\,}\eta}}= \frac{\xi-{\mathsf E\,}\xi}{\sqrt{{\mathsf D\,}\smash[b]{\xi\mathstrut}}}, \qquad \eta=\frac{\sqrt{\mathstrut{\mathsf D\,}\eta}}{\sqrt{{\mathsf D\,}\smash[b]{\xi\mathstrut}}}\,\xi+{\mathsf E\,}\eta -\frac{\sqrt{\mathstrut{\mathsf D\,}\eta}}{\sqrt{{\mathsf D\,}\smash[b]{\xi\mathstrut}}}\,{\mathsf E\,}\xi=a\xi+b.$

В случае $\rho(\xi,\,\eta)=-1$ нужно рассмотреть первое неравенство в формуле (19) и повторить рассуждения. Тем самым теорема 33 доказана.

Полезно знать следующие часто употребляемые термины.

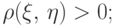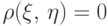Определение 41. Говорят, что $\xi$ и $\eta$ отрицательно коррелированы если $\rho(\xi,\,\eta)<0;$ положительно коррелированы, если $\rho(\xi,\,\eta)>0;$ некоррелированы, если $\rho(\xi,\,\eta)=0$ .

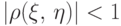Смысл знака $\rho(\xi,\,\eta)$ хорошо виден в случае $\rho(\xi,\,\eta)=\pm 1$ . Тогда знак $\rho$ равен знаку в равенстве $\eta=a\xi+b$ п.н. Так, $\rho(\xi,\,\eta)=1$ означает, что чем больше $\xi$ , тем больше и $\eta$ . Напротив, $\rho(\xi,\,\eta)=-1$ означает, что чем больше $\xi$ , тем меньше $\eta$ . Похожим образом можно трактовать знак коэффициента корреляции и в случае, когда $|\rho(\xi,\,\eta)|< 1$ , помня при этом, что зависимость между $\xi$ и $\eta$ теперь уже не линейная и, возможно, даже не функциональная.

Так, величины $\xi$ и $\xi+\eta$ в примерах 65 и 66 положительно коррелированы, но их зависимость не функциональная.

Следующее свойство показывает, что модуль коэффициента корреляции не меняется при линейных преобразованиях случайных величин.

Свойство 20. Для любых случайных величин $\xi$ и $\eta$ с конечной и ненулевой дисперсией при любых постоянных $a\ne 0$ и имеет место равенство

$\rho(a\xi+b,\,\eta)=\textup{sgn}\mspace{1mu}(a)\cdot \rho(\xi,\,\eta),$

где $\textup{sgn}\mspace{1mu}(a)=\frac{a}{|a|}$ - знак

.

Доказательство. Запишем $\rho(a\xi+b,\,\eta)$ , не забывая про свойства дисперсии:

$\qquad\rho(a\xi+b,\,\eta)=\frac{{{\rm cov}}(a\xi+b,\,\eta)}{\sqrt{\vphantom{a^2}{\mathsf D\,}(a\xi+b)}\,\sqrt{\vphantom{a^2}{\mathsf D\,}\eta}}= \frac{a\,{{\rm cov}}(\xi,\,\eta)}{\sqrt{a^2{\mathsf D\,}\xi}\,\sqrt{\vphantom{a^2}{\mathsf D\,}\eta}}= \frac{a}{|a|}\cdot \rho(\xi,\,\eta).\qquad$

Дальше >>

Авторизоваться

Введение в теорию вероятностей

Числовые характеристики зависимости

Коэффициент корреляции

Вопросы и ответы