Числовые характеристики зависимости
Примеры
Пример 67.
Если  и
и  суть координаты точки, брошенной
наудачу в треугольник
суть координаты точки, брошенной
наудачу в треугольник  с вершинами
с вершинами  ,
, 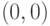 и
и 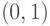 ,
то их коэффициент корреляции
,
то их коэффициент корреляции  отрицателен.
Это можно объяснить так: чем больше
отрицателен.
Это можно объяснить так: чем больше  , тем
меньше у
, тем
меньше у  возможностей быть большой.
возможностей быть большой.
Полезно убедиться в этом, проверив справедливость следующих высказываний. Во-первых,
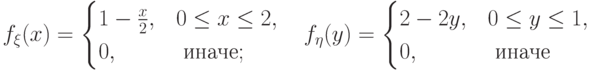
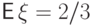 и
и  .
.Во-вторых, по определению многомерного равномерного распределения в
области  ,
,
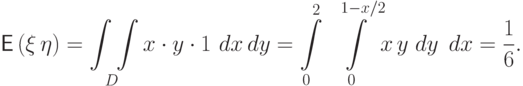
Пример 68.
Найдем коэффициент корреляции между числом выпадений единицы и числом
выпадений шестерки при  подбрасываниях правильной игральной
кости.
подбрасываниях правильной игральной
кости.
Обозначим для 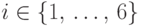 через
через 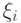 случайную величину,
равную числу выпадений грани с
случайную величину,
равную числу выпадений грани с  очками при
очками при  подбрасываниях
кубика.
Посчитаем
подбрасываниях
кубика.
Посчитаем 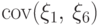 .
Каждая из случайных величин
.
Каждая из случайных величин 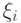 имеет биномиальное
распределение с параметрами
имеет биномиальное
распределение с параметрами  и
и  ,
поэтому
,
поэтому 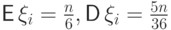 .
.
Далее заметим, что  .
Из-за симметрии кубика математические
ожидания
.
Из-за симметрии кубика математические
ожидания 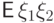 ,
, 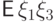 ,
, 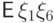 одинаковы, но отличаются от
одинаковы, но отличаются от 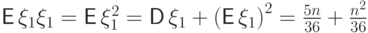 .
Посчитаем
.
Посчитаем  .
С одной стороны, это число равно
.
С одной стороны, это число равно
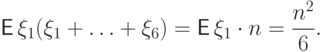
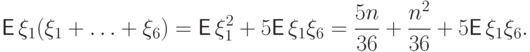
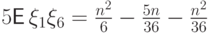 , т.е.
, т.е. 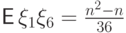 .
Следовательно, искомый коэффициент корреляции равен
.
Следовательно, искомый коэффициент корреляции равен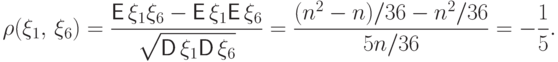
 .
.Пример 69. Вычислим математическое ожидание и дисперсию гипергеометрического распределения. Мы не могли сделать это раньше, так как очень не хотели вычислять следующие суммы:

 таким, что
таким, что 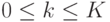 и
и 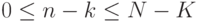 .
.Рассмотрим урну, содержащую  белых шаров и
белых шаров и  не белых, и пусть
из нее наудачу и без возвращения выбирают по одному
не белых, и пусть
из нее наудачу и без возвращения выбирают по одному  шаров.
Свяжем случайную величину
шаров.
Свяжем случайную величину  , равную числу белых шаров среди
, равную числу белых шаров среди  выбранных,
с результатами отдельных извлечений шаров.
выбранных,
с результатами отдельных извлечений шаров.
Обозначим через 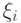 , где
, где 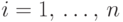 ,
"индикатор" того,
что
,
"индикатор" того,
что  -й по счету вынутый шар оказался белым:
-й по счету вынутый шар оказался белым: 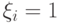 , если при
, если при  -м извлечении появился белый
шар, иначе
-м извлечении появился белый
шар, иначе  .
Тогда
.
Тогда 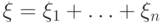 - число появившихся белых шаров,
и математическое
ожидание считается просто:
- число появившихся белых шаров,
и математическое
ожидание считается просто:
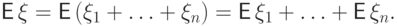
Убедимся, что случайные величины 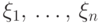 имеют
одно и то же
распределение Бернулли
имеют
одно и то же
распределение Бернулли 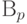 , где
, где 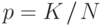 .
.
Пронумеруем шары: белые - номерами от одного до  ,
остальные - номерами от
,
остальные - номерами от 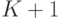 до
до  .
Элементарным исходом опыта является набор из
.
Элементарным исходом опыта является набор из  номеров шаров в
схеме
выбора
номеров шаров в
схеме
выбора  элементов из
элементов из  без возвращения и с учетом
порядка.
Общее число исходов равно
без возвращения и с учетом
порядка.
Общее число исходов равно 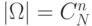 .
.
Вычислим вероятность события  . Событие
. Событие  включает в себя
элементарные исходы (наборы), в которых на
включает в себя
элементарные исходы (наборы), в которых на  -м месте стоит любой
из
номеров белых шаров, а остальные
-м месте стоит любой
из
номеров белых шаров, а остальные  место занимают любые из
оставшихся
место занимают любые из
оставшихся 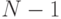 номеров. По теореме 1
о перемножении шансов число благоприятных
событию
номеров. По теореме 1
о перемножении шансов число благоприятных
событию  исходов есть произведение
исходов есть произведение  и
и 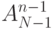 .
Здесь
.
Здесь  есть число способов поставить
на
есть число способов поставить
на  -е место один из номеров белых шаров,
-е место один из номеров белых шаров, 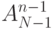 - число способов после этого
разместить на оставшихся
- число способов после этого
разместить на оставшихся  местах остальные
местах остальные 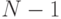 номеров
шаров. Но тогда
номеров
шаров. Но тогда
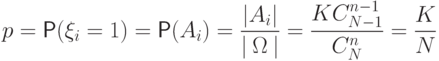
Вернемся к математическому ожиданию:
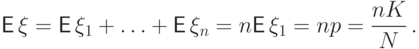
Вычислим дисперсию  .
До сих пор мы не интересовались совместным распределением
.
До сих пор мы не интересовались совместным распределением 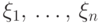 :
для вычисления математического ожидания их суммы нам было достаточно знания
маргинальных распределений этих величин. Но дисперсия суммы уже не всегда
равна сумме дисперсий. Зависимость величин
:
для вычисления математического ожидания их суммы нам было достаточно знания
маргинальных распределений этих величин. Но дисперсия суммы уже не всегда
равна сумме дисперсий. Зависимость величин 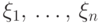 очевидна:
если, скажем, случилось событие
очевидна:
если, скажем, случилось событие  , то вероятность
второму шару быть
белым уже не равна отношению
, то вероятность
второму шару быть
белым уже не равна отношению 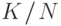 :
:
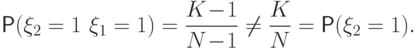
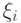 и
и 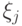 ,
, 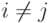 . Для этого сначала посчитаем
. Для этого сначала посчитаем  .
Произведение
.
Произведение 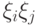 снова имеет распределение Бернулли:
снова имеет распределение Бернулли: 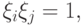 если при
если при 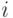 -м и
-м и 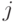 -м извлечениях появились белые шары.
Вероятность этого события равна
-м извлечениях появились белые шары.
Вероятность этого события равна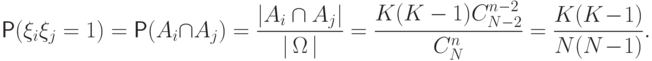
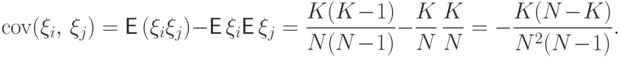
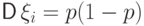 и эти не
зависящие от
и эти не
зависящие от  и
и  ковариации в формулу дисперсии суммы, получаем
ковариации в формулу дисперсии суммы, получаем![{\mathsf D\,}\xi &=&{\mathsf D\,}(\xi_1+\ldots+\xi_n)=
\sum\limits_{i=1}^n{\mathsf D\,}\xi_i + \sum\limits_{i\ne j}{{\rm cov}}(\xi_i,\xi_j)= \\
&=&np(1-p)+n(n-1){{\rm cov}}(\xi_1,\,\xi_2)=\\[2mm]
&=&n\,\frac{K}{N}\Bigl(1-\frac{K}{N}\Bigr)-
n(n\mspace{1mu}{-}\mspace{1mu}1)\frac{K(N\mspace{1mu}{-}\mspace{1mu}K)}{N^{2\mathstrut}(N\mspace{1mu}{-}\mspace{1mu}1)}
=n\,\frac{K}{N}\Bigl(1-\frac{K}{N}\Bigr)\Bigl(1-\frac{n\mspace{1mu}{-}\mspace{1mu}1}{N\mspace{1mu}{-}\mspace{1mu}1}\Bigr).](/sites/default/files/tex_cache/31f24511030c575375166f992e4268a9.png)
Заметим любопытнейшую вещь: если вынимать шары с возвращением, то
испытания станут независимыми испытаниями в схеме Бернулли; cтавшие
независимыми величины 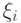 в сумме дадут число белых
шаров, имеющее биномиальное распределение с параметрами
в сумме дадут число белых
шаров, имеющее биномиальное распределение с параметрами  и
и 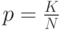 и точно такое же математическое ожидание
и точно такое же математическое ожидание  ,
как и у числа белых шаров при выборе без возвращения}.
,
как и у числа белых шаров при выборе без возвращения}.
Дисперсия же у числа белых шаров при выборе без возвращения меньше,
чем при выборе с возвращением - за счет отрицательной
коррелированности
слагаемых 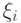 и
и 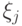 при
при 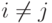 .
.
