Многомерные распределения
Независимость случайных величин
Как всегда, предполагается заданным вероятностное пространство 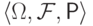 , на котором
определены все рассматриваемые случайные величины.
, на котором
определены все рассматриваемые случайные величины.
Определение 31.
Случайные величины  называют
независимыми
(в совокупности),
если для любого набора борелевских множеств
называют
независимыми
(в совокупности),
если для любого набора борелевских множеств 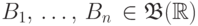 имеет место равенство
имеет место равенство
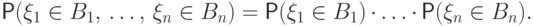
Определение 32.
Случайные величины 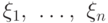 называют попарно
независимыми
если независимы любые две из них.
называют попарно
независимыми
если независимы любые две из них.
Оба этих определения годятся не только для конечного набора случайных величин, но и для их бесконечной последовательности.
Замечание
Независимость случайных величин в совокупности влечет попарную независимость.
Достаточно в определении независимости в качестве "лишних"
борелевских множеств взять  .
.
Пример 44.
Вспомним пример Бернштейна 32. Свяжем
с событиями  ,
,  и
и  случайные величины
случайные величины 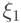 ,
, 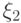 и
и  - индикаторы этих событий. Например,
- индикаторы этих событий. Например, 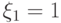 , если
, если  произошло, и
произошло, и  ,
если
,
если  не произошло.
Случайные величины
не произошло.
Случайные величины 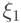 ,
, 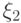 и
и  независимы попарно (проверить),
но зависимы в совокупности:
независимы попарно (проверить),
но зависимы в совокупности:
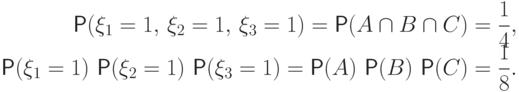
Попарная независимость случайных величин встречается редко. Поэтому всюду, где мы будем употреблять термин "независимы", будет подразумеваться независимость в совокупности.
Определение независимости можно сформулировать в терминах функций распределения.
Определение 33.
Случайные величины  независимы
(в совокупности),
если для любых
независимы
(в совокупности),
если для любых 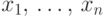 имеет место равенство
имеет место равенство
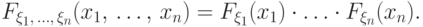
Описать независимость случайных величин с дискретным распределением можно с помощью таблицы их совместного распределения.
Определение 34.
Случайные величины  с дискретным распределением независимы
(в совокупности),
если для любых чисел
с дискретным распределением независимы
(в совокупности),
если для любых чисел 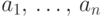 имеет место равенство
имеет место равенство

Упражнение. Доказать, что из независимости в смысле определения 31 следует независимость в смысле определения 33.
Упражнение. Доказать, что для случайных величин с дискретным распределением определения 31 и 34 эквивалентны.
Для случайных величин с абсолютно непрерывными распределениями справедливо утверждение.
Теорема 25. Случайные величины  с абсолютно непрерывными распределениями
независимы (в совокупности) тогда и только тогда, когда
плотность их совместного распределения существует
и равна произведению плотностей,
т.е. для любых
с абсолютно непрерывными распределениями
независимы (в совокупности) тогда и только тогда, когда
плотность их совместного распределения существует
и равна произведению плотностей,
т.е. для любых 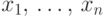 имеет место равенство:
имеет место равенство:  .
.
Замечание Плотность распределения определяется с точностью до ее значений на множестве нулевой лебеговой меры (распределение не меняется от изменения плотности на множестве нулевой меры). Поэтому равенство плотности совместного распределения и произведения плотностей можно понимать тоже как равенство "почти всюду".
Доказательство.
Пусть случайные величины  независимы,
т.е. для любых
независимы,
т.е. для любых 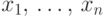
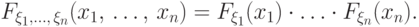
 -мерным интегралом:
-мерным интегралом:![\begin{multiline*}
F_{\xi_1}(x_1)\cdot\ldots\cdot F_{\xi_n}(x_n)=
\int\limits_{-\infty}^{x_1}\!\! f_{\xi_1}(s_1)\,ds_1 \,\cdot\,
\ldots\,\cdot\!\int\limits_{-\infty}^{x_n}\!\!
f_{\xi_n}(s_n)\,ds_n\,=\\[2pt]
=\!\int\limits_{-\infty}^{\,x_1}
\!{\ldots}\!\int\limits_{-\infty}^{\,x_n} f_{\xi_1}(s_1)\,
\ldots\,
f_{\xi_n}(s_n)\,\,ds_1\,\dots\,ds_n=F_{\xi_1,\dots,\,\xi_n}(x_1,\,\dots,\,x_n).=I_2. \;
\end{multiline*}](/sites/default/files/tex_cache/874f7ba243dd03285a5e451e8692273b.png)
Пусть теперь известно, что плотность совместного распределения существует и распадается в произведение плотностей. В таком случае функция совместного распределения распадается в произведение функций распределения: