НОУ ИНТУИТ | Введение в теорию вероятностей. Лекция 7: Основные семейства распределений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Новосибирский Государственный Университет

Опубликован: 07.04.2008 | Доступ: свободный | Студентов: 7252 / 1307 | Оценка: 4.56 / 4.32 | Длительность: 16:54:00

Тема: Математика

Специальности: Математик

Теги: алгебра, вычисления, графика, дискретное распределение, замечательный предел, коэффициент асимметрии, несовместное событие, полная группа, распределение бернулли, распределение коши, распределение пуассона, формула полной вероятности, функция Эйлера, цвета, элементы

|

Вам нравится? Нравится 73 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Примеры абсолютно непрерывных распределений

Равномерное распределение. Говорят, что $\xi$ имеет равномерное распределение на отрезке $[a,\,b]$ , и пишут: $\xi \sim U_{a,b}$ , если плотность распределения $\xi$ постоянна на отрезке $[a,\,b]$ и равна нулю вне него:

$f_\xi(x)=\begin{cases} \frac{1}{b-a}, & \textrm{\, если\, } x\in[a,\,b], \cr \,0, & \textrm{\, если\, } x\not\in[a,\,b]. \end{cases}$

Площадь под графиком этой функции равна единице, $f_\xi(x)\ge 0$ . Поэтому $f_\xi(x)$ является плотностью распределения.

Случайная величина $\xi \sim U_{a,b}$ имеет смысл координаты точки, выбранной наудачу на отрезке $[a,\,b]$ . Вычислим функцию распределения случайной величины $\xi$ :

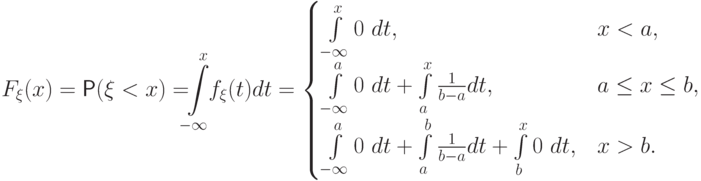
$F_\xi(x)=\Prob(\xi<x)=\!\!\!\int\limits_{-\infty}^x \!\!f_\xi(t) dt= \begin{cases} \int\limits_{-\infty}^x 0\ dt, & x < a, \cr \int\limits_{-\infty}^a 0\ dt +\int\limits_{a}^x \frac{1}{b-a} dt, & a\le x\le b, \cr \int\limits_{-\infty}^a 0\ dt+ \int\limits_{a}^b \frac{1}{b-a} dt+\int\limits_{b}^x 0\ dt, & x>b. \end{cases}$

Графики плотности и функции распределения равномерного распределения на отрезке [a, b]

изображены на рис. 7.1

Рис. 7.1. Плотность и функция распределения Ua, b

Заметьте, что в точках и функция распределения недифференцируема, и плотность можно задать как угодно.

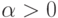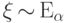Показательное распределение. Говорят, что $\xi$ имеет показательное (экспоненциальное) распределение с параметром $\alpha>0$ , и пишут: $\xi{\,\sim\,}{\mathrm E}_\alpha$ , если $\xi$ имеет следующую плотность распределения:

$f_\xi(x)=\begin{cases} 0, & \text{ если }\, x < 0, \cr \alpha e^{-\alpha x}, & \text{ если }\, x\ge 0. \end{cases}$

Функция распределения случайной величины $\xi$ непрерывна:

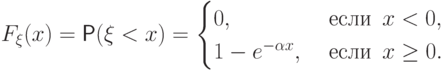
$F_\xi(x)=\Prob(\xi<x)=\begin{cases} 0, & \text{ если }\, x < 0, \cr 1-e^{-\alpha x}, & \text{ если }\, x\ge 0. \end{cases}$

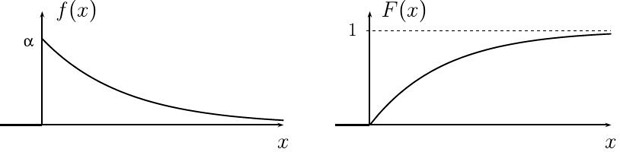
Графики плотности и функции распределения показательного распределения с параметром $\alpha$ приведены на рис. 7.2

Рис. 7.2. Плотность и функция распределения

Плотность показательного распределения равна нулю на отрицательной полуоси, поэтому вероятность события 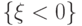$\{\xi < 0\}$ нулевая - случайная величина с показательным распределением не может быть отрицательна. К тому же плотность отлична от нуля на всей положительной полуоси, поэтому случайная величина с показательным распределением может принимать сколь угодно большие положительные значения: для всякого вероятность события $\{\xi>x\}$ не равна нулю.

Показательное распределение является единственным абсолютно непрерывным распределением, для которого выполнено свойство "нестарения" (и в этом смысле оно является непрерывным аналогом дискретного геометрического распределения).

Теорема 23. Пусть 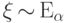$\xi{\,\sim\,}{\mathrm E}_\alpha$ . Тогда для любых $x,\,y>0$

$\begin{equation} \Prob(\xi>x+y | \xi>x)=\Prob(\xi>y). \end{equation}$

( 7.1)

Нормальное распределение. Говорят, что $\xi$ имеет нормальное (гауссовское) распределение с параметрами и $\sigma^2$ , где $a\in\mathbb R$ , $\sigma>0$ , и пишут: $\xi{\,\sim\,}{\mathrm N}_{a,\,\sigma^2}$ , если $\xi$ имеет следующую плотность распределения:

$f_\xi(x)=\frac{1}{\sigma\sqrt{2\pi}} e^{-\tfrac{(x-a)^2}{2\sigma^2}}, \quad x\in\mathbb R.$

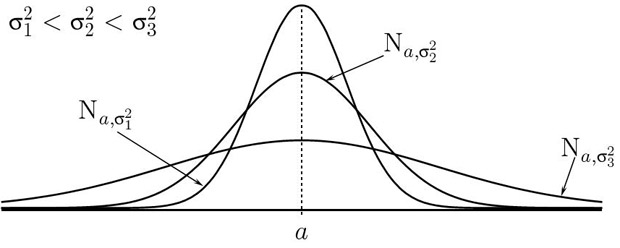
На рис. 7.3 приведены графики плотностей нормальных распределений с одним и тем же параметром и разными значениями параметра $\sigma$ .

Рис. 7.3. Плотности нормальных распределений

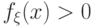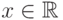Убедимся, что $f_\xi(x)$ является плотностью распределения. Так как $f_\xi(x)>0$ для всех $x\in\mathbb R$ , то свойство (f1) выполнено. Проверим (f2):

$\begin{multiple} \int\limits_{-\infty}^\infty f_\xi(x)\,dx&=& \int\limits_{-\infty}^\infty \frac{1}{\sigma\sqrt{2\pi}}~ e^{-\tfrac{(x-a)^2}{2\sigma^2}}\,dx= \left[\begin{array}{c}\text{ замена переменных } \cr t=\frac{x-a}{\sigma}, \, dx=\sigma\,dt \end{array}\right]\, =\\\int\limits_{-\infty}^\infty \frac{1}{\sigma\sqrt{2\pi}}~ e^{-t^2/2}\sigma\,dt= \frac{1}{\sqrt{2\pi}}~ \int\limits_{-\infty}^\infty e^{-t^2/2}\,dt\,=\frac{I}{\sqrt{2\pi}}\,=1, \end{multiple}$

где через

обозначен табличный интеграл (интеграл Пуассона)

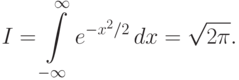
$I=\int\limits_{-\infty}^\infty e^{-x^2/2}\,dx=\sqrt{2\pi}.$

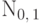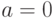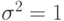Нормальное распределение ${\mathrm N}_{0,\,1}$ с параметрами a=0 и $\sigma^2=1$ называется стандартным нормальным распределением. Плотность стандартного нормального распределения равна $f_\xi(x)=\frac{1}{\sqrt{2\pi}}\,e^{-x^2/2}$ .

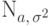Мы будем использовать специальное обозначение $\Phi_{a,\,\sigma^2}(x)$ для функции распределения нормального закона ${\mathrm N}_{a,\,\sigma^2}\vphantom{a^{a^a}}$ ( рис. 7.3). Первообразная функции $e^{-x^{\smash{2}}}$ не может быть выражена через элементарные функции. Поэтому функцию $\Phi_{a,\,\sigma^2}(x)$ можно записать лишь в виде интеграла

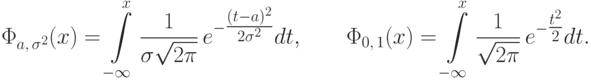
$\Phi_{a,\,\sigma^2}(x)=\int\limits_{-\infty}^x \frac{1}{\sigma\sqrt{2\pi}}\,e^{-\tfrac{(t-a)^2}{2\sigma^2}} dt, \qquad \Phi_{0,\,1}(x)=\int\limits_{-\infty}^x\frac{1}{\sqrt{2\pi}}\,e^{-\tfrac{t^2}{2}} dt.$

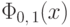Функция $\Phi_{0,\,1}(x)$ табулирована, т.е. ее значения при различных вещественных

вычислены. Их можно найти в соответствующих таблицах.

Дальше >>

Авторизоваться

Введение в теорию вероятностей

Основные семейства распределений

Примеры абсолютно непрерывных распределений

Вопросы и ответы