НОУ ИНТУИТ | Введение в теорию вероятностей. Лекция 6: Случайные величины и их распределения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Новосибирский Государственный Университет

Опубликован: 07.04.2008 | Доступ: свободный | Студентов: 7243 / 1307 | Оценка: 4.56 / 4.32 | Длительность: 16:54:00

Тема: Математика

Специальности: Математик

Теги: алгебра, вычисления, графика, дискретное распределение, замечательный предел, коэффициент асимметрии, несовместное событие, полная группа, распределение бернулли, распределение коши, распределение пуассона, формула полной вероятности, функция Эйлера, цвета, элементы

|

Вам нравится? Нравится 73 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Распределения случайных величин

Определение 22. Распределением случайной величины $\xi$ называется вероятностная мера $\mu(B)=\Prob(\xi\in B)$ на множестве борелевских подмножеств $\mathbb R$ .

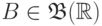Можно представлять себе распределение случайной величины $\xi$ как соответствие между множествами $B\in\mathfrak{B}(\mathbb R)$ и вероятностями $\Prob(\xi\in B)$ .

Распределения случайных величин суть основные объекты изучения в теории вероятностей. Мы не будем, как правило, интересоваться тем, из какого множества действует функция и каким именно элементарным исходам сопоставляет свои возможные значения. Нас будет интересовать лишь, с какой вероятностью эти значения принимаются. Приведем несколько примеров совершенно разных случайных величин, имеющих одно и то же распределение (одинаково распределенных).

Пример 39. Один раз бросается правильная монета. Пространство $\Omega$ состоит из двух элементарных исходов - герб и решка. В качестве $\sigma$ -алгебры рассмотрим множество всех подмножеств $\Omega$ , вероятность зададим как в классической схеме. Положим

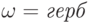$\xi(\omega)=1$ , если $\omega=\textit{герб}$ , и $\xi(\omega)=0$ , если $\omega = \textit{решка};$

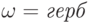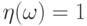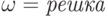$\eta(\omega)=0$ , если $\omega=\textit{герб}$ , и $\eta(\omega)=1$ , если $\omega = \textit{решка}$ .

Очевидно, что для любого множества 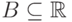$B\subseteq \mathbb R$ вероятности принадлежать для $\xi$ и для $\eta$ одинаковы. Тем не менее ни для одного элементарного исхода $\omega$ значения $\xi(\omega)$ и $\eta(\omega)$ не совпадают. Иными словами, $\xi$ и $\eta$ одинаково распределены, но не одинаковы как функции.

Пример 40. Точка наудачу бросается на отрезок $[0,\,1]$ . В этом случае $\Omega$ есть отрезок $[0,\,1]$ с $\sigma$ -алгеброй борелевских подмножеств $[0,\,1]$ и мерой Лебега в качестве вероятности. Читатель убедится, что две совершенно разные функции: $\xi(\omega)=\omega$ и $\eta(\omega)=1-\omega$ (расстояния до упавшей точки от левого и от правого концов отрезка соответственно) обладают одинаковыми вероятностями принимать значения внутри любых борелевских множеств . Вероятности эти равны мере Лебега пересечения множеств и $[0,\,1]$ . 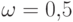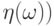Эти случайные величины одинаково распределены, но не одинаковы: их значения совпадают лишь при одном элементарном исходе $\omega= 0{,}5$ $\xi(\omega)$ и $\eta(\omega))$ .

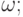
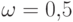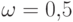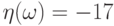Пример 41. На том же отрезке $\Omega=[0,\,1]$ построим две функции: ${\xi(\omega)=0}$ при всех $\omega;$ $\eta(\omega)=0$ при всех $\omega$ , кроме $\omega= 0{,}5$ , а в точке $\omega= 0{,}5$ положим $\eta(\omega)= -17$ .

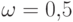Поскольку мера Лебега точки (она же - вероятность) равна нулю, распределения величин $\xi$ и $\eta$ одинаковы. Теперь $\xi(\omega)$ и $\eta(\omega)$ снова не совпадают как функции, но отличаются их значения лишь на множестве нулевой вероятности - только в точке $\omega= 0{,}5$ . В этом случае говорят, что $\xi$ и $\eta$ совпадают "почти наверное": $\Prob(\xi=\eta)=1$ .

Опишем различные типы распределений случайных величин. Вся вероятностная масса может быть сосредоточена в нескольких точках прямой, а может быть "размазана" по некоторому интервалу или по всей прямой. В зависимости от типа множества, на котором сосредоточена вся единичная вероятностная масса, распределения делят на дискретные, абсолютно непрерывные, сингулярные и их смеси.

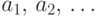Определение 23. Случайная величина $\xi$ имеет дискретное распределение, если существует конечный или счетный набор чисел $a_1,\,a_2,\,\dots$ такой, что

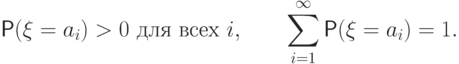
$\Prob(\xi=a_i)>0 \text{ для всех } i, \qquad \sum_{i=1}^{\smash{\infty}} \Prob(\xi=a_i)=1.$

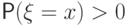Итак, случайная величина $\xi$ имеет дискретное распределение, если она принимает не более чем счетное число значений. Значения эти иначе называют атомами: $\xi$ имеет атом в точке , если $\Prob(\xi=x)>0$ .

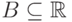
Если случайная величина $\xi$ имеет дискретное распределение, то для любого $B\subseteq\mathbb R$

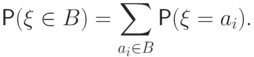
$\Prob(\xi\in B)=\sum\limits_{a_i\in B}\Prob(\xi=a_i).$

Дискретное распределение удобно задавать следующей таблицей, в которой 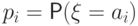$p_i=\Prob(\xi=a_i)$ :

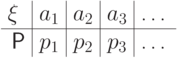
$\qquad\begin{tabular}{l|c|c|c|c} $\xi$ & $a_1$ & $a_2$ & $a_3$ & \ldots \cr \hline $\vphantom{\int^a}\Prob$ & $p_1$ & $p_2$ & $p_3$ & \ldots \end{tabular}$

Определение 24. Cлучайная величина $\xi$ имеет абсолютно непрерывное распределение, если существует неотрицательная функция $f_\xi(x)$ такая, что для любого борелевского множества

имеет место равенство:

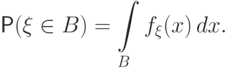
$\Prob(\xi\in B)=\int\limits_B f_\xi(x)\,dx.$

Функцию $f_\xi(x)$ называют плотностью распределения величины $\xi$ .

Замечание. Интеграл выше есть интеграл Лебега, а не Римана. Вполне достаточно, если читатель, не знакомый с интегралом Лебега, будет представлять его себе просто как площадь под графиком подынтегральной функции над множеством . При этом площадь над множеством , имеющим нулевую меру Лебега, равна нулю. Заметим, что любая функция, отличающаяся от функции $f_\xi(x)$ лишь в конечном или счетном числе точек (или на множестве нулевой меры Лебега), будет являться плотностью того же распределения, так как интеграл не изменится от изменения подынтегральной функции на множестве меры нуль.

Теорема 19. Плотность распределения обладает свойствами:

(f1) 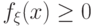$f_\xi(x)\ge 0$ для любого ;

(f2) 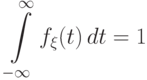$\displaystyle\int\limits_{-\infty}^\infty f_\xi(t)\,dt=1$ .

Доказательство. Свойство (f1) выполнено по определению плотности, свойство (f2) также следует из определения 24. Действительно, если в качестве борелевского множества взять всю числовую прямую, получим:

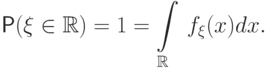
$\quad\Prob(\xi\in \mathbb R)=1=\int\limits_{\mathbb R}\, f_\xi(x) dx. \quad$

Эти два свойства полностью характеризуют класс плотностей.

Дальше >>

Авторизоваться

Введение в теорию вероятностей

Случайные величины и их распределения

Распределения случайных величин

Вопросы и ответы