Схема Бернулли
Независимые испытания с несколькими исходами
Рассмотрим схему независимых испытаний уже не с двумя, а с большим количеством возможных результатов в каждом испытании.
Пример 36. Игральная кость подбрасывается 15 раз. Найти вероятность того, что выпадет ровно десять троек и три единицы.
Здесь каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение любой другой грани. Поэтому воспользоваться формулой для числа успехов в схеме Бернулли не удаcтся.
Попробуем вывести подходящую формулу.
Пусть в одном испытании возможны  исходов:
исходов: 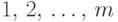 ,
и
,
и  -й исход в одном испытании
случается с вероятностью
-й исход в одном испытании
случается с вероятностью 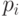 , где
, где  .
.
Обозначим через 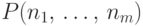 вероятность того, что
в
вероятность того, что
в  независимых испытаниях первый исход случится
независимых испытаниях первый исход случится 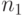 раз, второй исход -
раз, второй исход - 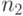 раз, и т.д., наконец,
раз, и т.д., наконец,  -й исход -
-й исход - 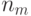 раз.
раз.
Теорема 16.
Для любого  и любых неотрицательных целых чисел
и любых неотрицательных целых чисел 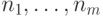 ,
сумма которых равна
,
сумма которых равна  , верна
формула
, верна
формула

Доказательство.
Рассмотрим один элементарный исход, благоприятствующий
выпадению 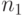 единиц,
единиц, 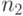 двоек и т.д.:
двоек и т.д.:

 экспериментов, когда все нужные исходы
появились в некотором заранее заданном порядке. Вероятность
такого результата равна произведению вероятностей
экспериментов, когда все нужные исходы
появились в некотором заранее заданном порядке. Вероятность
такого результата равна произведению вероятностей 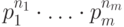 .
Остальные благоприятные исходы отличаются лишь расположением
чисел
.
Остальные благоприятные исходы отличаются лишь расположением
чисел  на
на  местах. Число таких
исходов
равно числу способов расположить на
местах. Число таких
исходов
равно числу способов расположить на  местах
местах 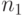 единиц,
единиц, 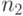 двоек, и т.д. Это число равно
двоек, и т.д. Это число равно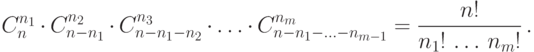
Теперь мы можем вернуться к примеру 36 и выписать ответ: вероятность получить десять троек, три единицы и еще два других очка равна

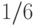 , а вероятность третьего исхода (выпала любая
другая грань)
равна
, а вероятность третьего исхода (выпала любая
другая грань)
равна 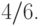
Теорема Пуассона для схемы Бернулли
Предположим, нам нужна вероятность получить не менее
семи успехов в тысяче испытаний схемы Бернулли с вероятностью
успеха  . Вероятность этого события равна любому
из следующих выражений, вычислить которые довольно сложно:
. Вероятность этого события равна любому
из следующих выражений, вычислить которые довольно сложно:

Сформулируем теорему о приближенном вычислении вероятности
иметь  успехов в большом числе испытаний Бернулли
с маленькой вероятностью успеха
успехов в большом числе испытаний Бернулли
с маленькой вероятностью успеха  . Термин "большое
число"
должен означать
. Термин "большое
число"
должен означать 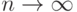 . Если при этом
. Если при этом  остается
неизменной,
то вероятность получить любое заданное число успехов
уменьшается до нуля. Необходимо чтобы
вероятность успеха
остается
неизменной,
то вероятность получить любое заданное число успехов
уменьшается до нуля. Необходимо чтобы
вероятность успеха  уменьшалась одновременно с ростом числа
испытаний. Но от испытания к испытанию вероятность успеха меняться
не может (см. определение схемы Бернулли). Поэтому нам придется
рассмотреть
так называемую "схему серий": если испытание одно, то вероятность
успеха в нем
равна
уменьшалась одновременно с ростом числа
испытаний. Но от испытания к испытанию вероятность успеха меняться
не может (см. определение схемы Бернулли). Поэтому нам придется
рассмотреть
так называемую "схему серий": если испытание одно, то вероятность
успеха в нем
равна 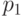 , если испытаний два, то вероятность успеха в каждом
равна
, если испытаний два, то вероятность успеха в каждом
равна 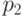 и т.д.
Если испытаний
и т.д.
Если испытаний  , то в каждом из них вероятность успеха равна
, то в каждом из них вероятность успеха равна  .
Вероятность успеха меняется не внутри одной серии испытаний,
а от серии к серии, когда меняется общее число испытаний.
Обозначим через
.
Вероятность успеха меняется не внутри одной серии испытаний,
а от серии к серии, когда меняется общее число испытаний.
Обозначим через 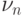 число успехов в
число успехов в  -й серии
испытаний.
-й серии
испытаний.
Теорема 17 (теорема
Пуассона).
Пусть 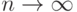 и
и 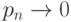 так, что
так, что  .
Тогда для любого
.
Тогда для любого  вероятность
получить
вероятность
получить  успехов
в
успехов
в  испытаниях схемы Бернулли с вероятностью успеха
испытаниях схемы Бернулли с вероятностью успеха  стремится к величине
стремится к величине 
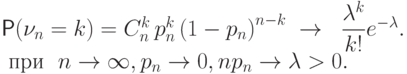
Доказательство.
Положим 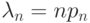 . По условию
. По условию 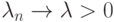 .
Подставим
.
Подставим  в формулу Бернулли:
в формулу Бернулли:
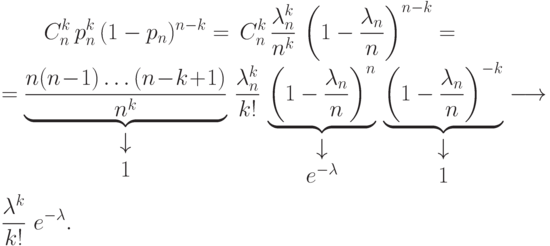 |
( 5.2) |
 и
замечательным пределом
и
замечательным пределом 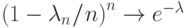 .
Докажем последнее свойство:
.
Докажем последнее свойство: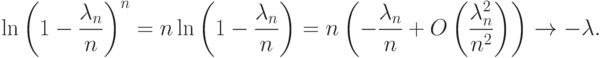
Определение 19.
Набор чисел  называется распределением Пуассона с параметром
называется распределением Пуассона с параметром 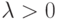 .
.
По теореме 17 можно приближенно посчитать
вероятность получить не менее
семи успехов в тысяче испытаний схемы Бернулли с вероятностью
успеха  , с вычисления которой мы начали.
Поскольку
, с вычисления которой мы начали.
Поскольку  "велико", а
"велико", а  "мало",
то, взяв
"мало",
то, взяв 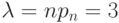 , можно записать приближенное равенство
, можно записать приближенное равенство
 |
( 5.3) |
Осталось решить, а достаточно ли  велико,
а
велико,
а  мало, чтобы заменить
точную вероятность на ее приближенное значение.
Для этого нужно уметь оценивать разницу между этими вероятностями.
мало, чтобы заменить
точную вероятность на ее приближенное значение.
Для этого нужно уметь оценивать разницу между этими вероятностями.
Следующую очень полезную теорему мы, исключительно из экономии времени, доказывать не станем.
Теорема 18 (уточненная теорема Пуассона).
Пусть  - произвольное множество целых
неотрицательных чисел,
- произвольное множество целых
неотрицательных чисел, 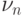 - число успехов в
- число успехов в  испытаниях
схемы Бернулли с вероятностью успеха
испытаниях
схемы Бернулли с вероятностью успеха  ,
,  .
Cправедливо неравенство
.
Cправедливо неравенство

Таким образом, теорема 18
предоставляет нам возможность
самим решать, достаточно ли  велико, а
велико, а  мало,
руководствуясь полученной величиной погрешности. Какова же погрешность
в формуле (5.3)? Взяв
мало,
руководствуясь полученной величиной погрешности. Какова же погрешность
в формуле (5.3)? Взяв  имеем
имеем

Таким образом, можно утверждать, что искомая вероятность заключена в границах 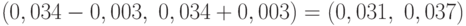 .
.
