Аксиоматика теории вероятностей
Мера и вероятностная мера
Определение 8.
Пусть  - некоторое непустое множество,
- некоторое непустое множество, 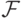 -
-  -алгебра его
подмножеств.
Функция
-алгебра его
подмножеств.
Функция  называется мерой на
называется мерой на 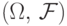 ,
если она удовлетворяет условиям:
,
если она удовлетворяет условиям:
( 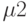 ) для любого счетного набора попарно
непересекающихся множеств
) для любого счетного набора попарно
непересекающихся множеств  (т.е. такого, что
(т.е. такого, что  при всех
при всех  )
мера их объединения равна сумме их мер:
)
мера их объединения равна сумме их мер:
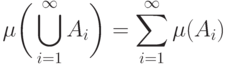
 -аддитивность" меры).
-аддитивность" меры).Упражнение.
Зачем в свойстве ( 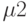 ) требуется, чтобы события не пересекались?
Может ли какая-нибудь функция
) требуется, чтобы события не пересекались?
Может ли какая-нибудь функция 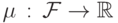 удовлетворять свойству
удовлетворять свойству  при любых событиях
при любых событиях  и
и  ? Привести пример такой
функции и доказать,
что других не существует.
? Привести пример такой
функции и доказать,
что других не существует.
Упражнение.
Указать область определения и область значений функции  . Для
каких
. Для
каких 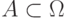 определено значение
определено значение 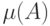 ?
?
Пример 25.
Пусть 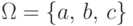 ,
,  -
множество всех
подмножеств
-
множество всех
подмножеств  . Зададим меру
. Зададим меру  на
на 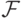 так:
так: 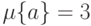 ,
, 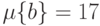 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 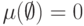 .
Для краткости записи мы вместо
.
Для краткости записи мы вместо 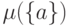 писали всюду
писали всюду  .
.
Пример 26.
Пусть 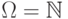 ,
,  -
множество всех
подмножеств натурального ряда. Зададим меру
-
множество всех
подмножеств натурального ряда. Зададим меру  на
на 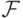 так:
так:  - число элементов в множестве
- число элементов в множестве  (бесконечность, если
множество
(бесконечность, если
множество  бесконечно).
бесконечно).
Пример 27. (мера Лебега)
Когда мы говорили о геометрической вероятности, мы использовали
термин "мера области  в
в 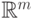 ", имея
в виду "длину" на прямой,
"площадь" на плоскости, "объем" в трехмерном
пространстве.
Являются ли все эти "длины-площади-объемы" настоящими мерами в
смысле
определения 8? Мы решим этот вопрос
для прямой, оставляя плоскость
и пространство большей размерности читателю.
", имея
в виду "длину" на прямой,
"площадь" на плоскости, "объем" в трехмерном
пространстве.
Являются ли все эти "длины-площади-объемы" настоящими мерами в
смысле
определения 8? Мы решим этот вопрос
для прямой, оставляя плоскость
и пространство большей размерности читателю.
Замечание Если вам уже расхотелось читать дальше, сообщаем: мерой Лебега в задачниках и учебниках называют как раз "длину-площадь-объем", так что все в порядке, дальнейшее до определения вероятности можно смело пропустить.
Рассмотрим вещественную прямую с  -алгеброй борелевских
множеств.
Эта
-алгеброй борелевских
множеств.
Эта  -алгебра, по определению, есть наименьшая
-алгебра, по определению, есть наименьшая  -алгебра, содержащая все интервалы.
Для каждого интервала
-алгебра, содержащая все интервалы.
Для каждого интервала 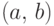 число
число  назовем длиной интервала
назовем длиной интервала 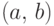 .
.
Мы не станем доказывать следующее утверждение:
Теорема 6.
Существует единственная мера  на
на 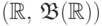 , значение которой
на любом
интервале равно его длине:
, значение которой
на любом
интервале равно его длине:  .
Эта мера называется мерой Лебега.
.
Эта мера называется мерой Лебега.
Нам пригодится свойство, которым обладает любая мера.
Это свойство непрерывности меры иногда называют аксиомой
непрерывности, имея в виду, что
ею можно заменить (  2) в определении 8.
2) в определении 8.
Теорема 7 (свойство непрерывности меры).
Пусть дана убывающая последовательность 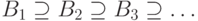 множеств из
множеств из 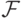 , причем
, причем  . Пусть
. Пусть  .
Тогда
.
Тогда 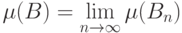 .
.
Доказательство.
Обозначим через  кольца:
кольца: 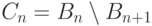 . Множества
. Множества  ,
, 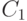 ,
, 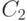 ,
,  попарно не пересекаются. Тогда из представлений
попарно не пересекаются. Тогда из представлений

 2), соответствующие равенства и для
мер:
2), соответствующие равенства и для
мер:
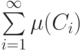 в силу условия
в силу условия  ,
есть сумма абсолютно сходящегося ряда (составленного из неотрицательных
слагаемых).
Из сходимости этого ряда следует, что "хвост" ряда, равный как
раз
,
есть сумма абсолютно сходящегося ряда (составленного из неотрицательных
слагаемых).
Из сходимости этого ряда следует, что "хвост" ряда, равный как
раз  , стремится к нулю при
, стремится к нулю при 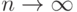 .
Поэтому
.
Поэтому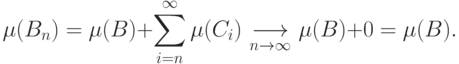
В полезности этого свойства легко убедиться упражнениями. Упражнение.
Используя аксиому непрерывности меры для убывающей последовательности
множеств  ,
доказать, что мера Лебега одноточечного подмножества
,
доказать, что мера Лебега одноточечного подмножества  вещественной прямой
равна нулю:
вещественной прямой
равна нулю:  . Используя этот факт, доказать, что
. Используя этот факт, доказать, что 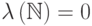 ,
,  ,
,  ,
, ![\lambda\,(a,\,b)=\lambda\,[\,a,\,b\,]](/sites/default/files/tex_cache/61021f0116d140f3f9d7ee54fce413aa.png) .
.
Замечание.
В отсутствие предположения  свойство
свойство 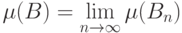 может не
выполняться.
может не
выполняться.
Например, зададим
меру на 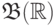 так:
так:  , если
, если  не более чем счетно, иначе
не более чем счетно, иначе 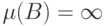 .
Тогда для множеств
.
Тогда для множеств  имеем:
имеем:
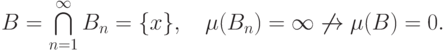
Наконец, мы в состоянии определить понятие вероятности как нормированной меры.
Определение 9.
Пусть  - непустое множество,
- непустое множество, 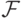 -
-  -алгебра его подмножеств.
Мера
-алгебра его подмножеств.
Мера  называется
нормированной,
если
называется
нормированной,
если 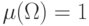 .
Другое название нормированной меры -
вероятность.
.
Другое название нормированной меры -
вероятность.

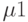 )
) 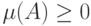 для любого
для любого