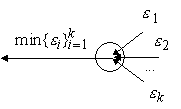Погрешности в нейронных сетях
Для адаптивного сумматора можно вычислять как допустимые погрешности входных сигналов сумматора, так и допустимые погрешности весов синапсов. Для вычисления допустимых погрешностей весов синапсов также можно использовать равномерное, пропорциональное и приоритетное распределение погрешностей. При равномерном распределении допустимые погрешности для весов синапсов вычисляются по формуле:

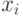 - входные сигналы сумматора.
- входные сигналы сумматора.При пропорциональном распределении допустимые погрешности для весов синапсов вычисляются по формуле:  , где
, где  - число входов сумматора,
- число входов сумматора, 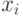 - входные сигналы сумматора.
- входные сигналы сумматора.
При приоритетном распределении сначала назначаются допустимые погрешности для тех весов синапсов, которые наиболее значимы по какому-либо признаку, а затем оставшуюся часть допустимой погрешности для выходного сигнала сумматора распределяют между оставшимися весами синапсов равномерно или пропорционально.
При обратном распространении точности имеет место специфическая двойственность - элементы сети заменяются на двойственные им. Однако, эта двойственность отличается от той, с которой мы встречаемся при изучении обратного распространения ошибки для вычисления градиентов функции оценки. Так, если в обычном обратном распространении двойственным элементом к точке ветвления является простой сумматор, то при обратном распространении точности вместо него, как было показано, появляется элемент, вычисляющий минимум приходящих на него сигналов. Нелинейный преобразователь при обратном распространении точности заменяется двойственным ему элементом, умножающим сигнал на число. Но если при обратном распространении ошибки множителем является значение градиента, то в нашем случае сигнал умножается на величину обратную производной от входного сигнала нелинейного преобразователя. Адаптивный сумматор также заменяется двойственным ему элементом. Этот элемент является своеобразной точкой ветвления. Но, в отличии от простой точки ветвления, он сначала преобразует приходящий к нему сигнал в соответствии с выбранным распределением погрешностей по входам адаптивного сумматора, а затем передает полученные сигналы дальше.
Теперь мы знаем, каким образом вычислять гарантированную интервальную оценку погрешности для любого элемента стандартного нейрона методом обратного распространения точности.
-
Точка ветвления. Если допустимые погрешности выходных сигналов точки ветвления равны
 , то в качестве погрешности входного сигнала точки ветвления выбирается
, то в качестве погрешности входного сигнала точки ветвления выбирается 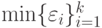 ( рис. 6.2).
( рис. 6.2).
-
Нелинейный преобразователь. Пусть при прямом функционировании входной сигнал нелинейного преобразователя равен
 , его выходной сигнал равен
, его выходной сигнал равен  и нелинейный преобразователь имеет функцию активации
и нелинейный преобразователь имеет функцию активации  . Если допустимая погрешность выходного сигнала нелинейного преобразователя равняется
. Если допустимая погрешность выходного сигнала нелинейного преобразователя равняется 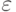 , то погрешность его входного сигнала не должна превышать
, то погрешность его входного сигнала не должна превышать  , где
, где ![x \in [\varphi^{- 1}(y - \varepsilon ),\varphi^{- 1}(y + \varepsilon )]](/sites/default/files/tex_cache/cb8254b3e97cd65b6571651b5ce2cd8a.png) или в линейном приближении
или в линейном приближении 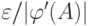 ( рис. 6.3).
( рис. 6.3).
-
Адаптивный сумматор. Если при обратном распространении допустимая погрешность выходного сигнала адаптивного сумматора равняется
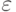 , то погрешность каждого входа сумматора не должна превышать
, то погрешность каждого входа сумматора не должна превышать 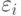 , где
, где 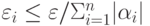 для равномерного распределения и
для равномерного распределения и  для пропорционального распределения ( рис. 6.4).
для пропорционального распределения ( рис. 6.4).